Tutorial 7: CLV - Non-contractual settings

Introduction: Latent Attrition

In this section, we’ll focus on non-contractual settings, where the time at which a customer dies, or becomes permanently inactive, is not observed by the firm. We will focus on one class of models called latent attrition or “Buy Til You Die” models. All these models share a common feature:

The customer’s relationship with a firm has two phases: a customer is active for some period of time, then becomes permanently inactive.

These models are a subset of Hidden Markov models where the two states-alive and dead-are not directly observed, hence hidden. The classic paper that launched this literature created the Pareto/NBD model, which is in continuous time.¹

A better place to start for us however is the Beta-geometric/Beta-binomial (BG/BB) model, because it is in discrete time and has building blocks similar to the sBG model we covered in the last session.

The BG/BB model

The best place to start off is the Beta-geometric/Beta-Binomial model (BG/BB), which is in discrete time. This is the same discrete time we used with the sBG (shifted Beta-geometric) model for contractual settings. The assumptions of the model are given in the research paper²:

1. A customer’s relationship with the firm has two phases: he is alive (A) for some period of time, then becomes permanently inactive (“dies”; D).

2. While alive, a customer makes a purchase with probability \(p\) in any given period: \[ P(Y(t) = 1 \mid p, \textrm{alive at} \; t) = p, \quad 0 \leq p \leq 1 \] This implies that a customer alive for \(s\) periods makes a number of purchases according to a Binomial\((s, p)\) distribution.

3. A “living” customer dies at the beginning of a transaction opportunity with probability . (This implies that the (unobserved) lifetime of a customer is characterized by a geometric distribution.³) \[ P( \textrm{alive at} \; t \mid \theta)= P(T>t \mid \theta) = S(t \mid \theta ) = (1-\theta)^t \qquad 0 \leq \theta \leq 1 \] As an aside, our one-step Markov transition matrix from alive to dead looks like: \[ T = \left(\begin{array}{cc} 1-\theta & \theta \\ 0 & 1 \end{array}\right) \] Given that the customer was alive last period (top row), a customer stays alive each period with probability \(1-\theta\), and dies with probability \(\theta\). If the customer was dead last period (bottom row), he or she remains dead with probability 1.

4. Heterogeneity in \(p\) follows a beta distribution with parameters \(\alpha\) and \(\beta\). \[ f(p \; | \; \alpha,\beta) = \frac{p^{\alpha-1} (1-p)^{\beta-1}}{B(\alpha,\beta)}, \qquad \alpha>0, \beta>0\]

5. Heterogeneity in \(\theta\) follows a beta distribution with parameters \(\gamma\) and \(\delta\). \[ f(\theta \; | \; \gamma,\delta) = \frac{\theta^{\gamma-1} (1-\theta)^{\delta-1}}{B(\gamma,\delta)}, \qquad \gamma>0, \delta>0\]

6. The purchase probability \(p\) and the dropout probability \(\theta\) vary independently across customers.

Likelihood BG/BB

The likelihood is a function of three summary statistics:

1. \(n\) transaction opportunities

2. \(t_x\), recency, the period of the last donation relative to the first donation. (This is opposite to how we usually think of recency, more below.)

3. \(x\), frequency, the total number of donations

For each \(\{n, t_x, x\}\), we sum over the possible hidden state realizations, alive and dead:

\[ L(\alpha, \beta, \gamma, \delta \mid n, t_x, x) = \underbrace{\frac{B(\alpha+x, \beta + n-x)}{B(\alpha, \beta)} \frac{B(\gamma, \delta + n)}{B(\gamma, \delta)}}_\text{alive all periods} + \underbrace{ \sum_{i=0}^{n-t_x-1} \; \frac{B(\alpha+x, \beta + t_x -x + i )}{B(\alpha, \beta)} \frac{B(\gamma+1, \delta + t_x+i)}{B(\gamma, \delta)}}_\text{all paths with death before end} \] If \(x=0, t_x=0\). This recency is measured as the time of last purchase from the beginning of the observation period; in the past we’ve measured recency as the time from last purchase until the end of the observation period (\(n-t_x\)).

If there was a donation in the last period, \(t_x=n\), then \(n-t_x-1=-1\), meaning the upper limit of the sum in the second term is lower than the lower limit, and by convention, the term drops out. This means that he/she must be alive at the end of the last period, since only alive customers can make donations. In that case,

\[ L(\alpha, \beta, \gamma, \delta \mid n, t_x=n, x) = \frac{B(\alpha+x, \beta + n-x)}{B(\alpha, \beta)} \frac{B(\gamma, \delta + n)}{B(\gamma, \delta)} \]

Loading the data

First we have to load the R package, BTYD and some auxiliary packages as well. You can download the package from here:

install.packages('https://cran.r-project.org/src/contrib/Archive/BTYD/BTYD_2.4.tar.gz', repos = NULL, type = "source")

You can load the package:

library("BTYD")
options("scipen"=100, "digits"=3, width = 300)

Load the donation data, and get the the calibration period recency-frequency matrix:

data(donationsSummary)

rf.matrix <- donationsSummary$rf.matrix
head(rf.matrix) %>% 
  kbl() %>%
  kable_styling()

x	t.x	n.cal	custs
6	6	6	1203
5	6	6	728
4	6	6	512
3	6	6	357
2	6	6	234
1	6	6	129

If \(f_j\) is the number of customers in each of the \(J\) recency-frequency cells in the rf.matrix as above (\(f_1 =\) 1203, \(f_2 =\) 728, …) the sample log likelihood is then:

\[ LL(\alpha, \beta, \gamma, \delta) = \sum_{j=1}^J f_j \log[L(\alpha, \beta, \gamma, \delta \mid n, t_x, x)] \]

We maximize this to find the parameters \(\{\alpha, \beta, \gamma, \delta\}\).

Here is the donation data we mentioned in the lecture. All donors in this cohort made their first donation in 1995. What we have is their repeat donation history 1996-2006. We fit the model to only the repeat data, not the first donation.

par(mfrow=c(1,1))
par(mai=c(.8,.8,.2,.2))
plot(seq(1996,2006,1),donationsSummary$annual.trans, type="b", ylab="Total number of repeat transactions", xlab="Year", main="", xaxt='n')
x.tickmarks.yrs.all <- c( "'96","'97","'98","'99","'00","'01","'02","'03","'04","'05","'06" )
#axis(1, at = seq(0, 11, by = 1))
axis(1, at=seq(1996,2006,1),labels = x.tickmarks.yrs.all)
abline(v=2001.5,col = "red", lwd = 2)
text(x = 1999,y = 5000,"Calibration", cex=1, pos=3, col="black", font = 2)
text(x = 2004,y = 5000,"Validation", cex=1, pos=3, col="black", font = 2)

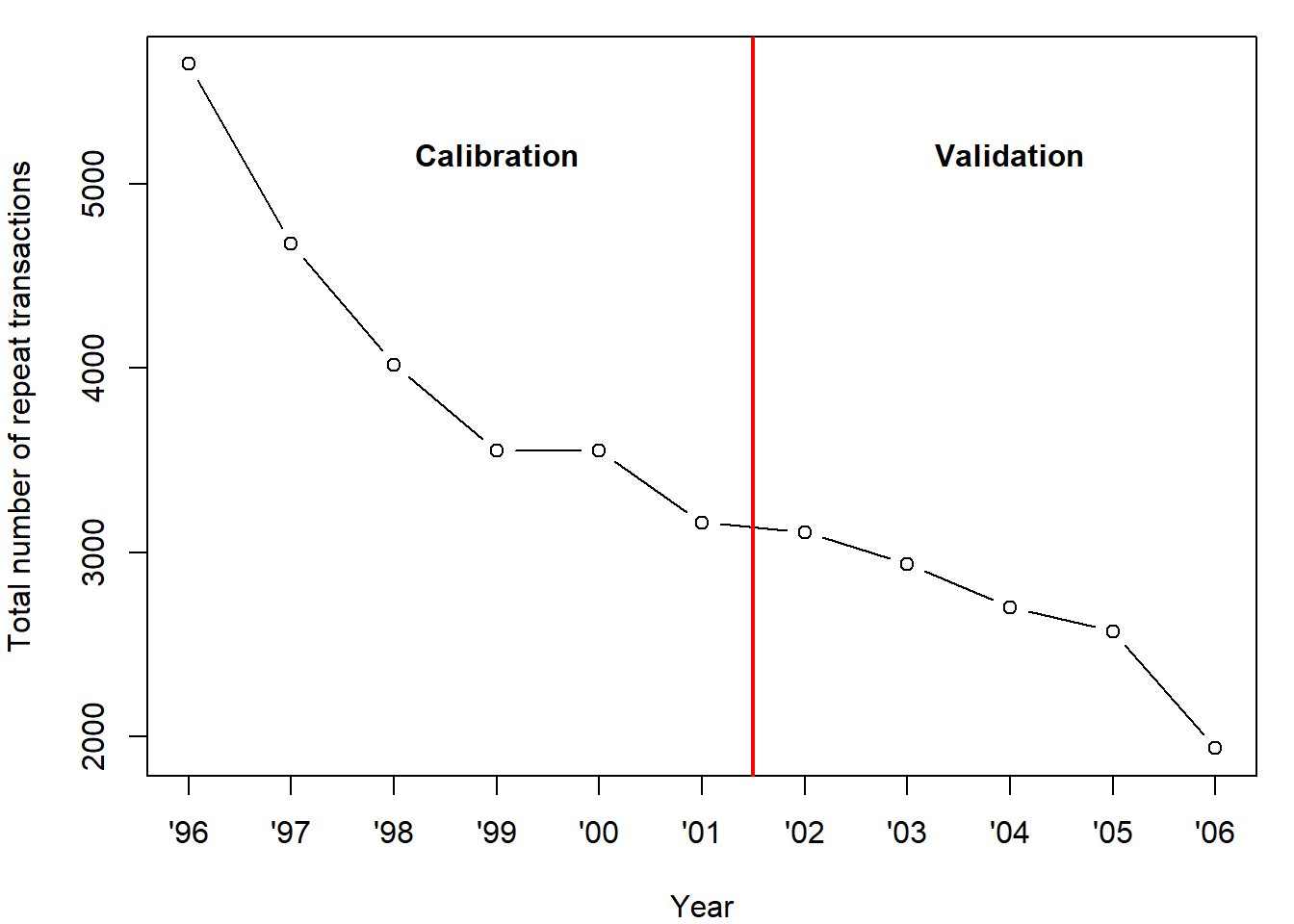
Our calibration data is 1996-2001, so it lasts 6 periods (\(n=6\)). We validate the model using years 2002-2006. All we need to estimate the model are the sufficient statistics:

• “reverse” recency (\(t_x\)): the last period a donation occurred. Since are data comprise 6 periods, the most recent donation is 6, or \(t_x=6\). If no repeat donations were observed, \(t_x = 0\). (Usually marketers think of recency as the number of periods since last purchase, \(n-t_x\). Here recency is time after first purchase.) Note further that if \(x=0, \; t_x=0\).
• frequency (\(x\)): the number of repeat donations observed in the six subsequent periods.
• number of purchase opportunities (\(n\)): this is usually the same for everyone. In this case \(n=6\).

There are 22 recency-frequency combinations. The number of customers in each cell is below.

You can see, for example, that there are 1203 customers who are “6 for 6”. And there are 3464 customers who made no repeat donations, “0 for 6”. The model is going to have to account for these differences.

Estimate parameters for the BG/BB model from the recency-frequency matrix:

We give initial guesses to the four parameters in par.start. bgbb.EstimateParameters estimates the parameters.

#            alpha beta gamma delta
par.start <- c(1, .5, 1, .5)

params <- bgbb.EstimateParameters(rf.matrix, par.start)

## store parameters next to names
names(params) <- c("alpha", "beta", "gamma", "delta");

round(params,2)

## alpha  beta gamma delta 
##  1.20  0.75  0.66  2.78

## Check log-likelihood of the params:
LL <- bgbb.rf.matrix.LL(params, rf.matrix)

Parameter Estimates and Distributions

We plot the beta distributions implied by the maximum likelihood estimates.

par(mfrow=c(1,2))
par(mai=c(.8,.8,.5,.2))
temp <- bgbb.PlotTransactionRateHeterogeneity(params)
par(mai=c(.8,.8,.5,.2))
temp <- bgbb.PlotDropoutRateHeterogeneity(params)

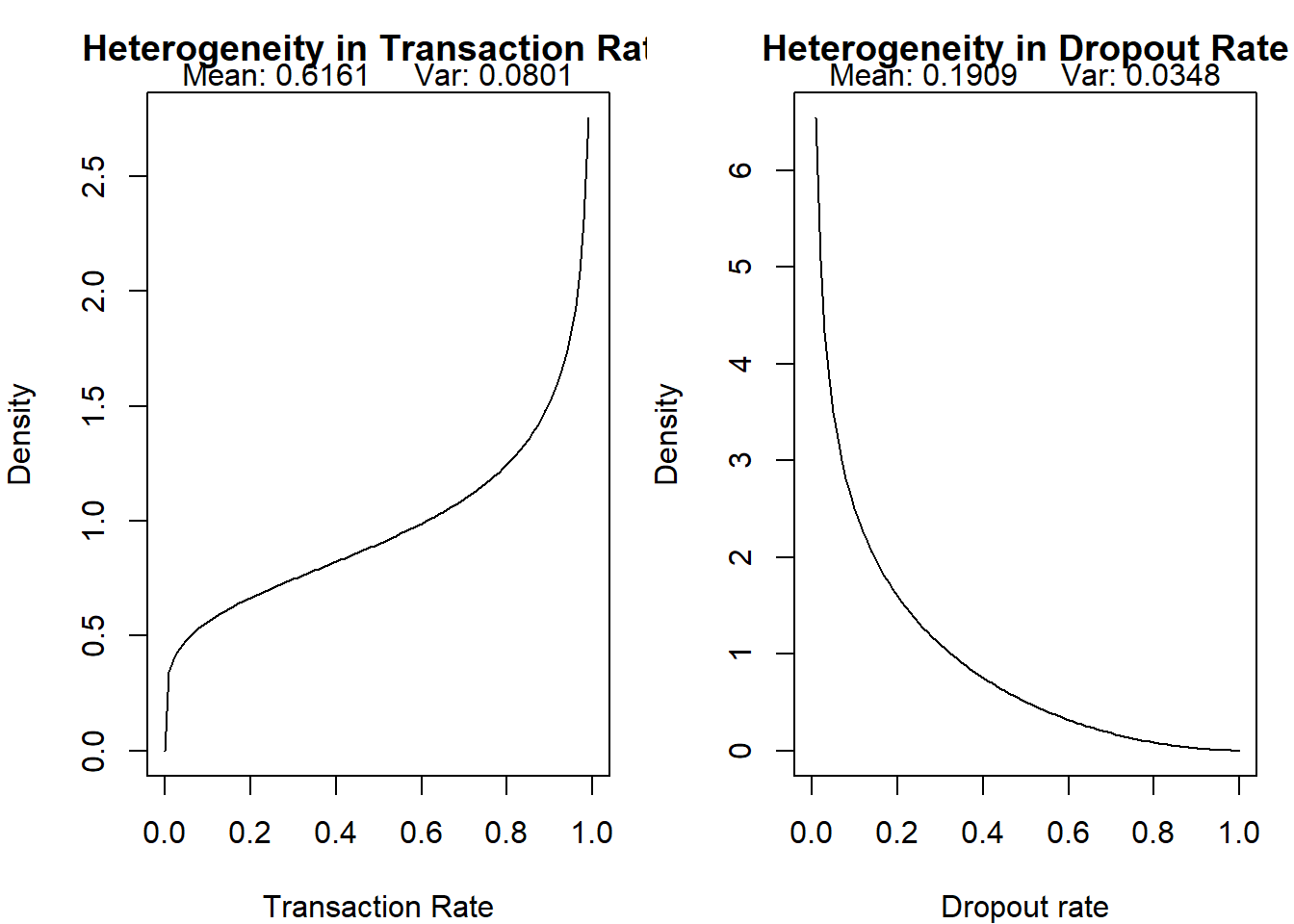
Remember, if \(X \sim \textrm{Beta}(a,b), \; E[X] = \frac{a}{a+b}\). So the mean of the transaction rate while alive is 0.62 and the mean of the drop out process is 0.19.

# Mean of transaction rate while alive:
params[1]/(params[1]+params[2])

## alpha 
## 0.616

# Mean of drop-out process:
params[3]/(params[3]+params[4])

## gamma 
## 0.191

Model fit

Aggregate

We can see how well the model does in predicting the aggregate number of donations over years. This uses equation 8 in the FHS (2010).

inc.annual.trans <- donationsSummary$annual.trans   # incremental annual transactions

par(mfrow=c(1,1))
## Plot the comparison of actual and expected total incremental transactions across
## both the calibration and holdout periods:
par(mai=c(.8,.8,.3,.2))

pred <- bgbb.PlotTrackingInc(params, rf.matrix, inc.annual.trans, xticklab=x.tickmarks.yrs.all)[2,]

text(x = 4,y = 5000,"Calibration", cex=1, pos=3, col="black", font = 2)
text(x = 7,y = 5000,"Validation", cex=1, pos=3, col="black", font = 2)

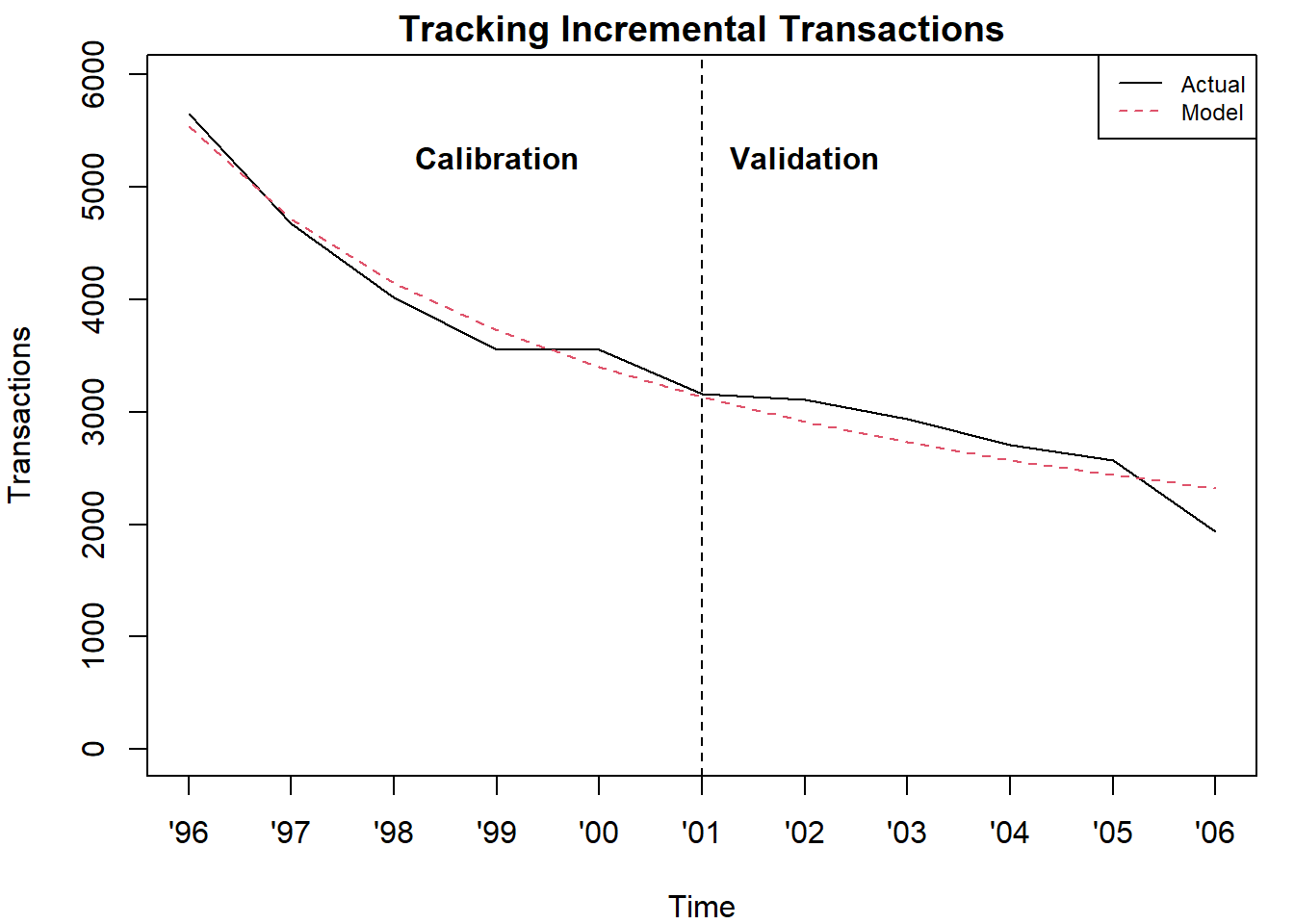
# The incremental transactions using the formula, equation 8, in the paper.  donations should equal pred above.

al <- params[1]
be <- params[2]
ga <- params[3]
de <- params[4]

nn <- seq(1,11)
N <- sum(rf.matrix[,4])
Eq8 <- (al/(al+be))*(de/(ga-1))*(1-(gamma(ga+de)*gamma(1+de+nn)/(gamma(ga+de+nn)*gamma(1+de))))

cum_donations <- N*Eq8
donations <- c(cum_donations[1],diff(cum_donations))

Here is for the cumulative number of donations.

par(mai=c(.8,.8,.3,.2))

pred <- bgbb.PlotTrackingCum(params, rf.matrix, actual.cum.repeat.transactions = cumsum(donationsSummary$annual.trans), xticklab=x.tickmarks.yrs.all)[2,]

text(x = 4,y = 5000,"Calibration", cex=1, pos=3, col="black", font = 2)
text(x = 7,y = 5000,"Validation", cex=1, pos=3, col="black", font = 2)

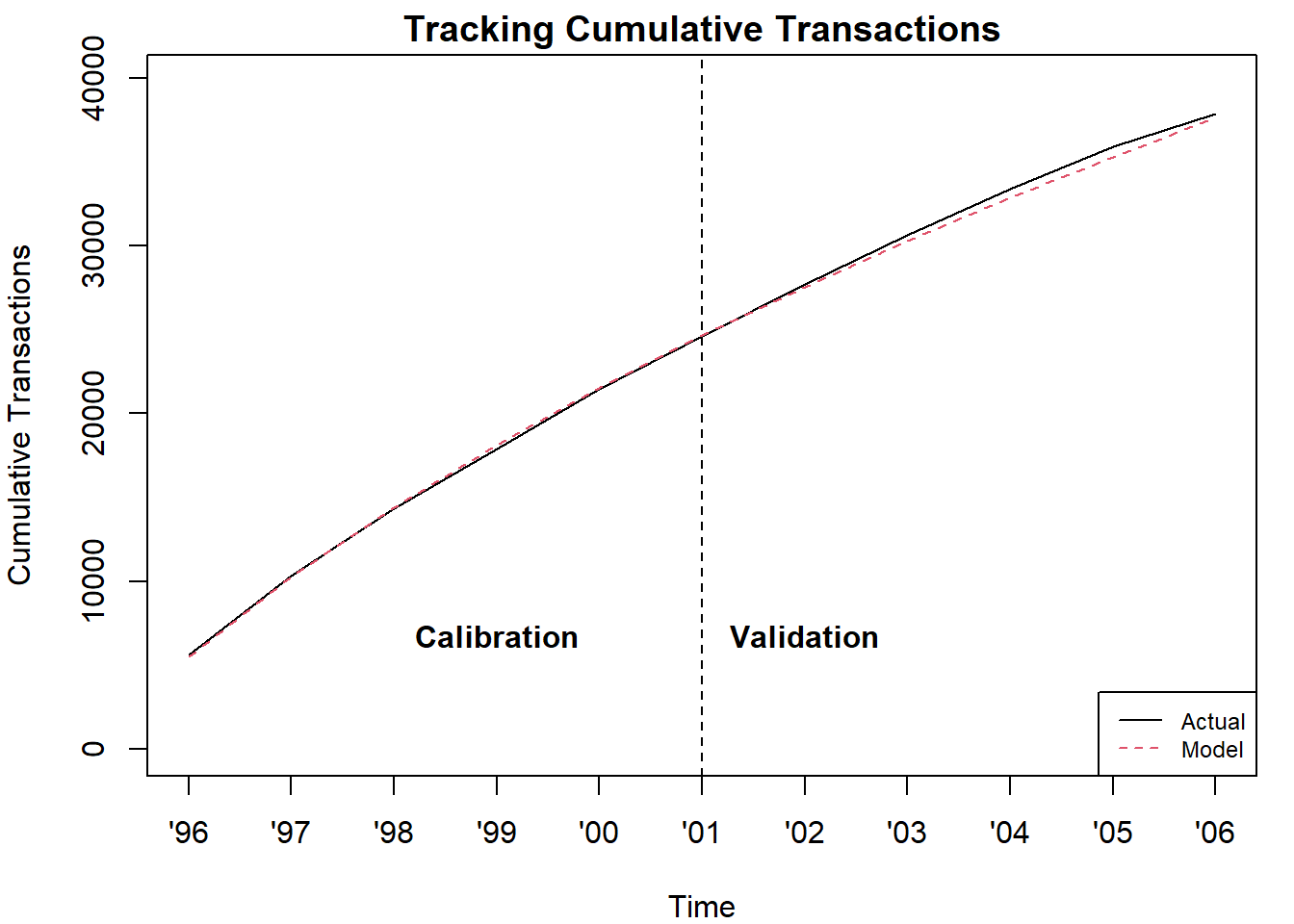
Conditional Expectations

A very important test of a model is how well it predicts at the individual level, after conditioning on a particular individual history. Given a customer with history \((x, t_x, n)\), (a) how many purchases do we predict in the next \(n^*\) periods and (b) how well does it track actual holdout purchases?

We first do (a). Using equation 13, we can calculate the expected number of purchases for each \((x, t_x, n)\) group in the next \(n^* = 5\) periods.

par(mai=c(.8,.8,.5,.2))
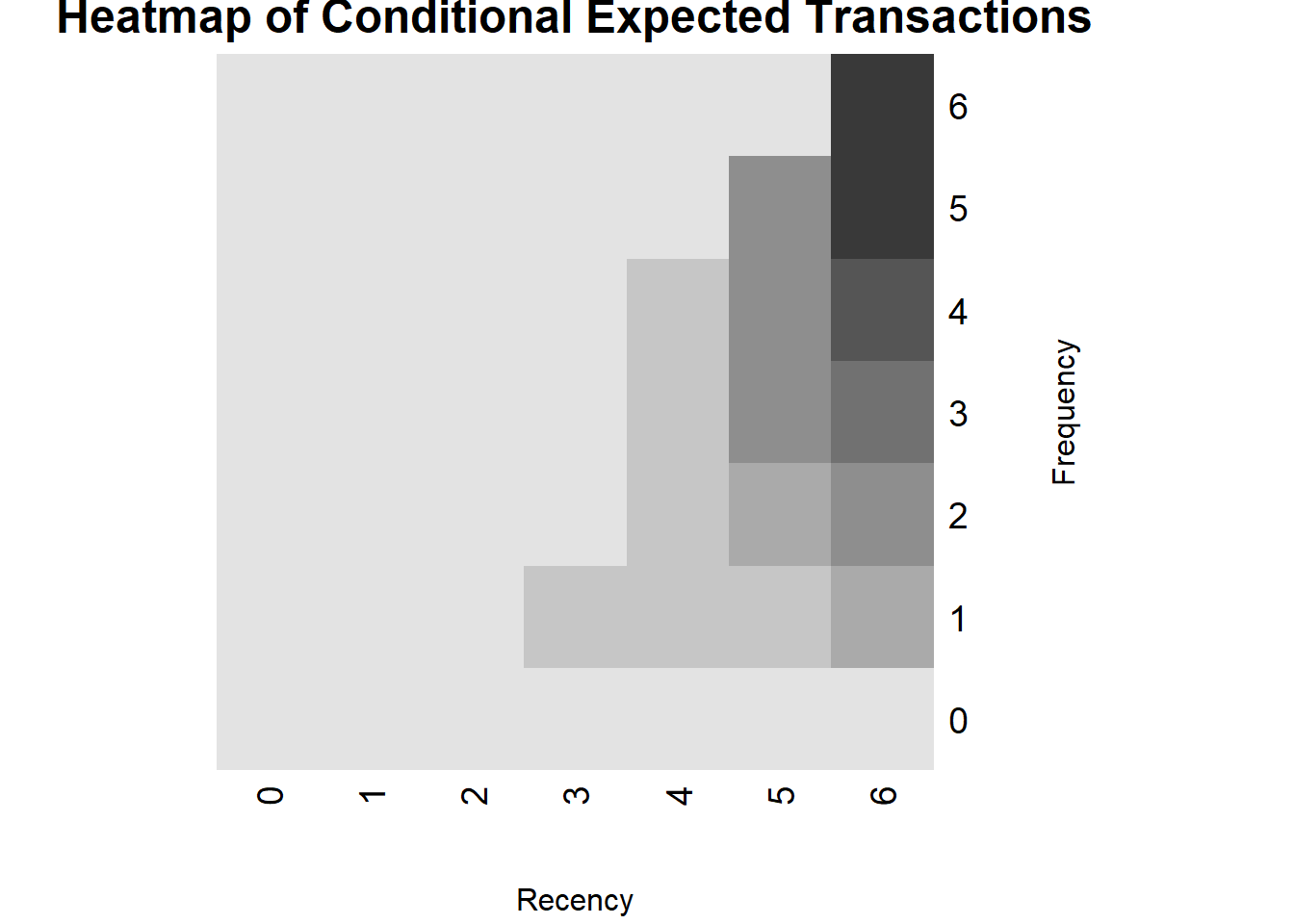
comp <- bgbb.HeatmapHoldoutExpectedTrans(params, n.cal=6, n.star=5)

## layout: widths =  0.05 4 , heights =  0.25 4 ; lmat=
##      [,1] [,2]
## [1,]    0    3
## [2,]    2    1

# rotate matrix so it's the same direction as the heatmap, this is just to make the numbers easier to read
rotate <- function(x) t(apply(x, 2, rev))
library(kableExtra)
test <- kable(rotate(rotate(rotate(t(round(comp,2))))), format = "pipe", booktabs=F, align = "c", caption = "**Predicted holdout purchases (BG/BB Model) based on frequency (rows) x recency (columns)**")

A donor who donated every year except the last \((x=5, t_x=5, n=6)\) is predicted to make 1.81 in the next \(n^*=5\) periods. Yet a donor with better recency but lower frequency \((x=4,t_x=6, n=6)\) has a higher expected transaction rate, 2.71. As mentioned in Fader, Hardie and Shang (2010), this highlights the importance of recency.

Now we do (b). The actual number of total holdout purchases by customers in each RF category is given in the variable x.star. Therefore the average number of holdout purchases per RF category is the total divided by the number of customers. We add this to the RF matrix and reshape.

n.star <- 5                        # Number of transaction opportunities in the holdout period
x.star <- donationsSummary$x.star  # Transactions made by each calibration period bin in the holdout period

X<-x.star/rf.matrix[,"custs"]

hol_rf_trans<-as.data.frame(cbind(rf.matrix[,1:2],X))

actual_rf<-reshape(hol_rf_trans, idvar="t.x", timevar="x", direction="wide")

# change NA's to 0
actual_rf[is.na(actual_rf)] <- 0

# re-order columns and rows
actual_rf<-actual_rf[order(actual_rf[,1]),order(actual_rf[1,])]

# make tx to rowname
rownames(actual_rf) <- actual_rf[,8]

# delete tx
actual_rf<-actual_rf[,c(-8)]

#actual_rf

# to make it look nice and rotated in same way as heatmap
kable(rotate(rotate(rotate((round(actual_rf,2))))), format = "pipe", booktabs=F, align = "c", caption = "**Actual holdout average purchases based on frequency (rows) x recency (columns)**")

Actual holdout average purchases based on frequency (rows) x recency (columns)

	0	1	2	3	4	5	6
X.6	0.00	0.00	0.00	0.00	0.00	0.00	3.53
X.5	0.00	0.00	0.00	0.00	0.00	1.74	3.06
X.4	0.00	0.00	0.00	0.00	0.84	1.91	2.72
X.3	0.00	0.00	0.00	0.46	0.94	1.66	2.29
X.2	0.00	0.00	0.40	0.46	0.74	1.41	1.89
X.1	0.00	0.22	0.37	0.60	0.56	1.14	1.47
X.0	0.17	0.00	0.00	0.00	0.00	0.00	0.00

Conditioning on frequency & recency separately

Next we can how well the model does if we condition on the frequency of transactions in the calibration period, averaging over recency. In other words, we take everyone who has had a frequency of \(x\) transactions in the calibration period, and we can compare how many actual transactions they had in the validation period with the predictions.

par(mai=c(.8,.8,.5,.2))

## Plot the comparison of actual and conditional expected holdout period frequencies,
## binned according to calibration period frequencies:
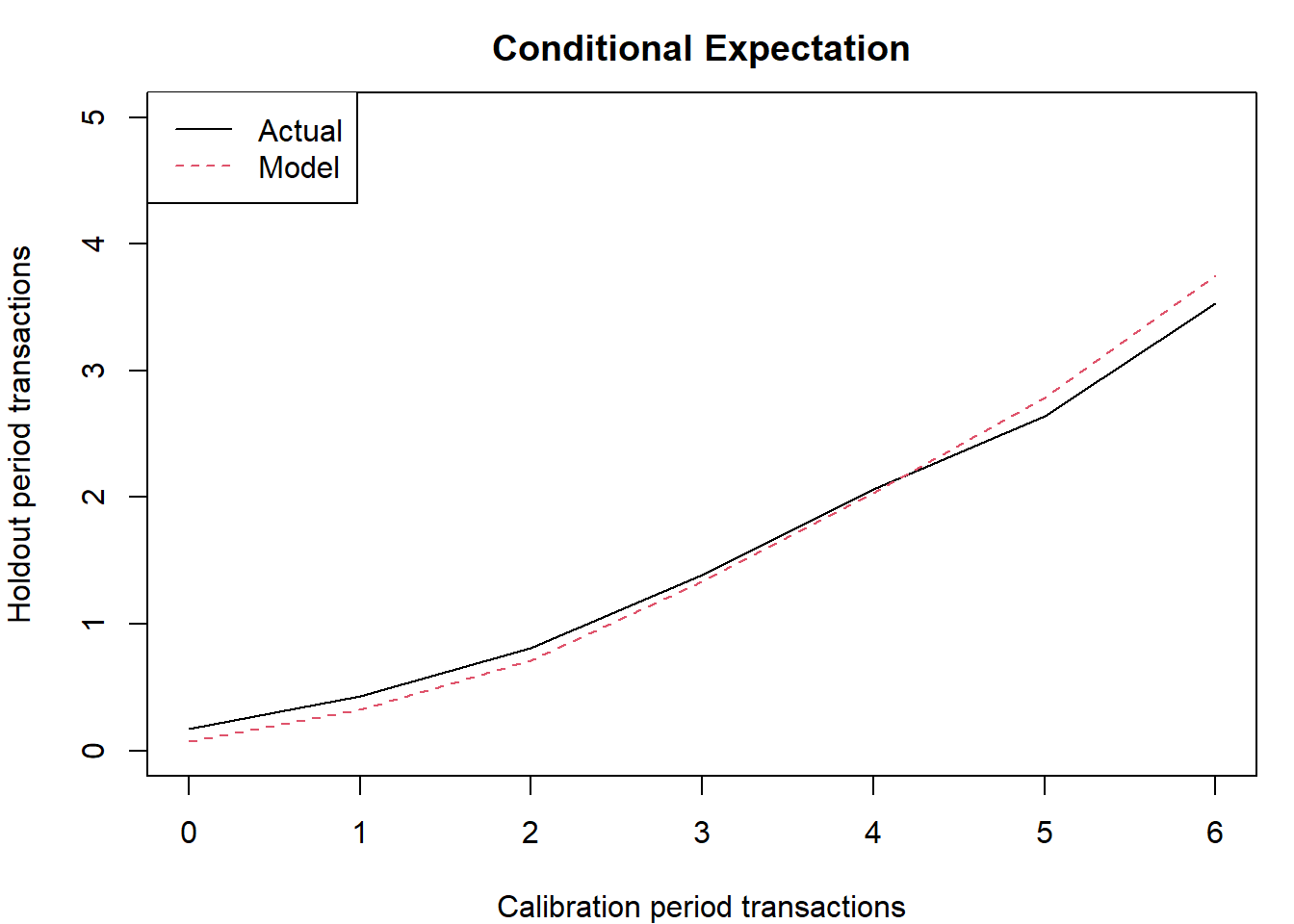
freq <- bgbb.PlotFreqVsConditionalExpectedFrequency(params, n.star, rf.matrix, x.star)

rownames(freq) <- c("act", "exp", "bin")
freq

##        freq.0   freq.1   freq.2  freq.3  freq.4  freq.5  freq.6
## act    0.1744    0.433    0.813    1.39    2.06    2.64    3.53
## exp    0.0729    0.325    0.709    1.33    2.03    2.78    3.75
## bin 3464.0000 1823.000 1430.000 1085.00 1036.00 1063.00 1203.00

Model predictions closely track actual donations. Donors who made zero donations 1996-2001, made on average 0.07 donations in 2002-2006. The BG/BB model predicts slightly fewer, 0. Donors who made a donation every year, “6 for 6”, made 0 donations in the subsequent 5 years. The model predictions are modestly higher, at 1.15. It’s interesting to note that a naive prediction of a donor who is “6 for 6” so would therefore be a “5 for 5” donor in the validation period would overestimate donations by quite a lot.

Instead of grouping customers by frequency, we can also condition on their recency, i.e., the last period they made a donation:

par(mai=c(.8,.8,.5,.2))

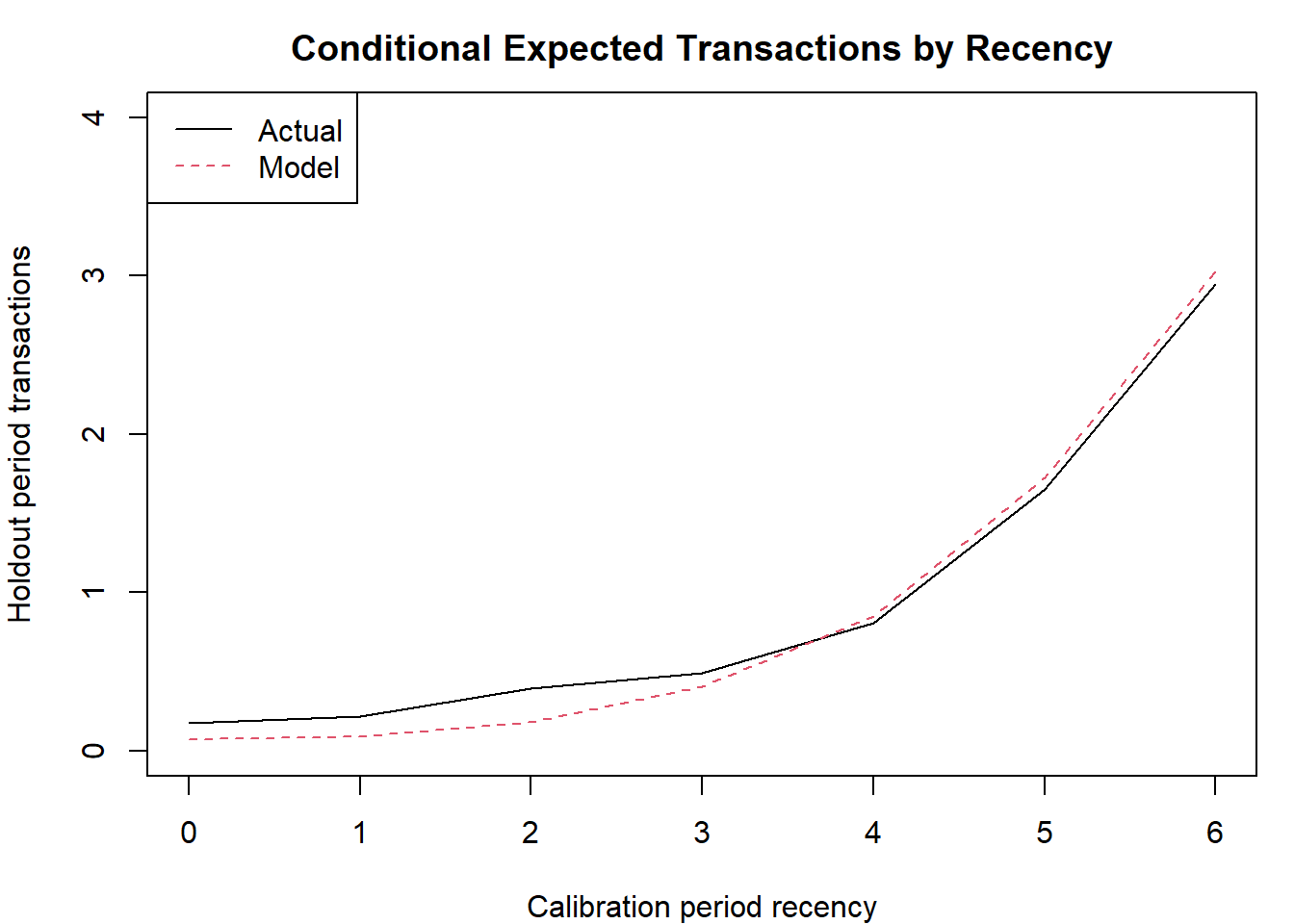
rec<-bgbb.PlotRecVsConditionalExpectedFrequency(params, n.star, rf.matrix, x.star)

rownames(rec) <- c("act", "exp", "bin")
rec

##         rec.0     rec.1  rec.2   rec.3   rec.4   rec.5   rec.6
## act    0.1744    0.2181   0.39   0.487   0.809    1.65    2.95
## exp    0.0729    0.0857   0.18   0.404   0.851    1.73    3.03
## bin 3464.0000 1091.0000 890.00 706.000 654.000 1136.00 3163.00

There were 1.669 donors with maximum recency, i.e., making a donation in 2001. Those donors made on average 0 donations in the subsequent 5 years, and the model predicts that they would make 1.1. There is a steep falloff as recency diminishes, moving from right to left in the graph that is captured by the model.

P(Alive)

The probability that a customer with purchase history \(x, t_x n\) will be alive at the beginning of period \(n + 1\) is the term in the likelihood where the customer is alive until the end divided by all the paths: \[ P(\textrm{Alive at} \; n+1 | \; n, x, t_x) = \frac{\frac{B(\alpha+x, \beta + n-x)}{B(\alpha, \beta)} \frac{B(\gamma, \delta + n+1)}{B(\gamma, \delta)}}{L(\alpha, \beta, \gamma, \delta \mid n, t_x, x)} \]

We can calculate for all the possible cells in our recency-frequency matrix the probability that the customer is active.

PAlive <- bgbb.PAlive(params, x = rf.matrix[,1], t.x = rf.matrix[,2], n.cal = 6)
Alive_mat<-cbind(rf.matrix,PAlive)
Alive_mat<-data.frame(Alive_mat)
kable(Alive_mat, format="pipe")

x	t.x	n.cal	custs	PAlive
6	6	6	1203	0.930
5	6	6	728	0.930
4	6	6	512	0.930
3	6	6	357	0.930
2	6	6	234	0.930
1	6	6	129	0.930
5	5	6	335	0.522
4	5	6	284	0.697
3	5	6	225	0.767
2	5	6	173	0.805
1	5	6	119	0.828
4	4	6	240	0.200
3	4	6	181	0.440
2	4	6	155	0.590
1	4	6	78	0.680
3	3	6	322	0.095
2	3	6	255	0.299
1	3	6	129	0.481
2	2	6	613	0.066
1	2	6	277	0.255
1	1	6	1091	0.069
0	0	6	3464	0.108

with(Alive_mat, hist(rep(x = Alive_mat$PAlive, times = Alive_mat$custs), xaxt='n', xlim = c(0,1), xlab = "P(Alive at n+1)", ylab="frequency", main="Histogram of P(Alive)"))
axis(side=1, at=seq(0,1, .10), labels=seq(0,1,.1))

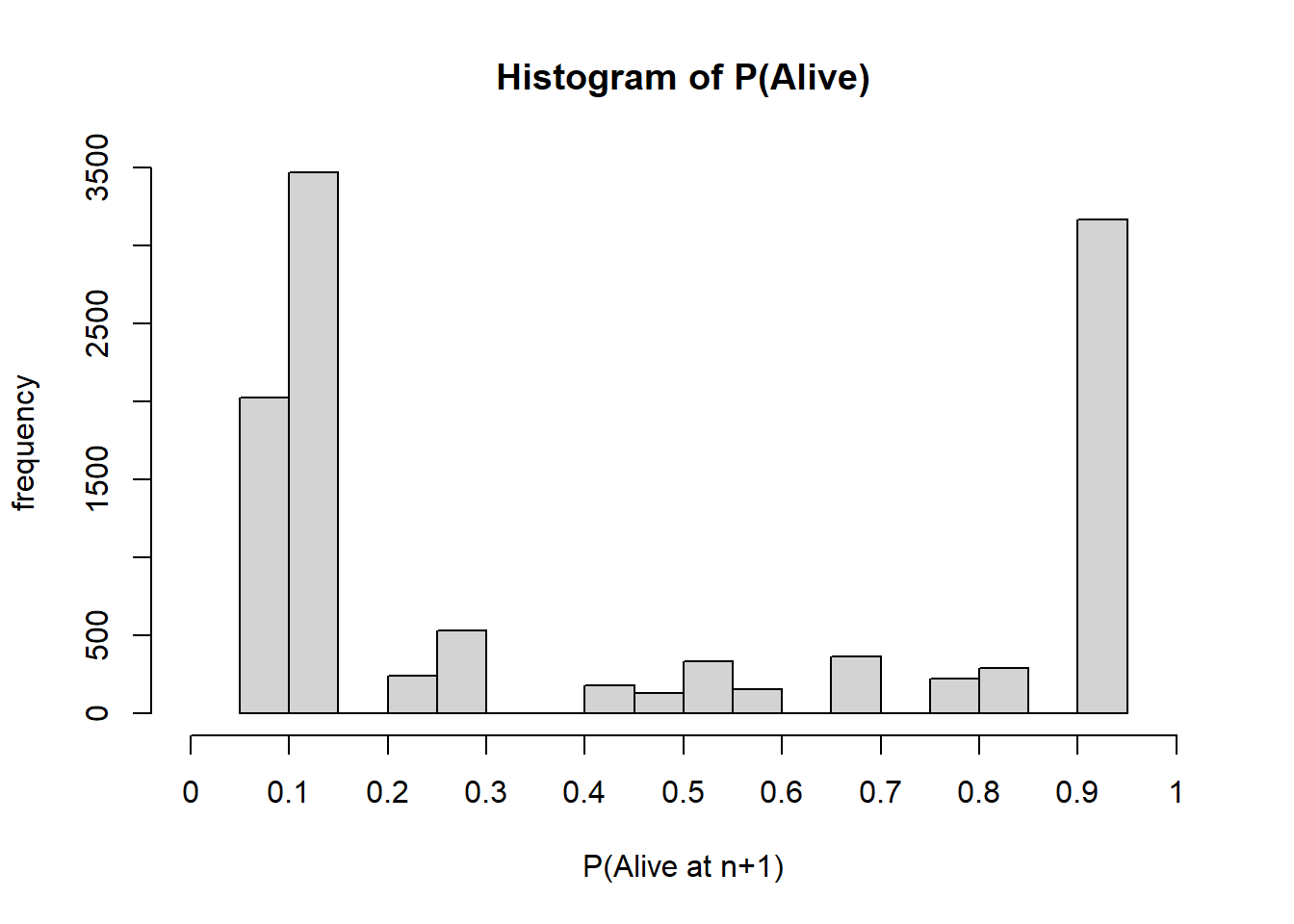
How many total active or alive customers are there at period 7? We can sum up all the P(Alive) cells and number of customers in each cell to get the answer:

sum(Alive_mat$PAlive*Alive_mat$custs)

## [1] 4728

There are 4728.494 out of 11104 customers still active.

Increasing Frequency Paradox

Let’s imagine a customer who has made his or her last donation on period \(t_x = 4\), but let’s vary how many purchases she makes. At most she can make 4, and at least 1. We can ask what the model predicts is the number of purchases expected in the subsequent \(n^*=5\) periods, a calculation we already did above:

par(mfrow=c(1,1),mai=c(.8,.8,.5,.2))
plot(comp[2:5,5], ylab ="Expected transactions in next 5 periods", xlab="Frequency holding last donation at 4", type="b", xaxt="n")
xtick<-seq(1, 4, by=1)
axis(side=1, at=xtick, labels = TRUE)

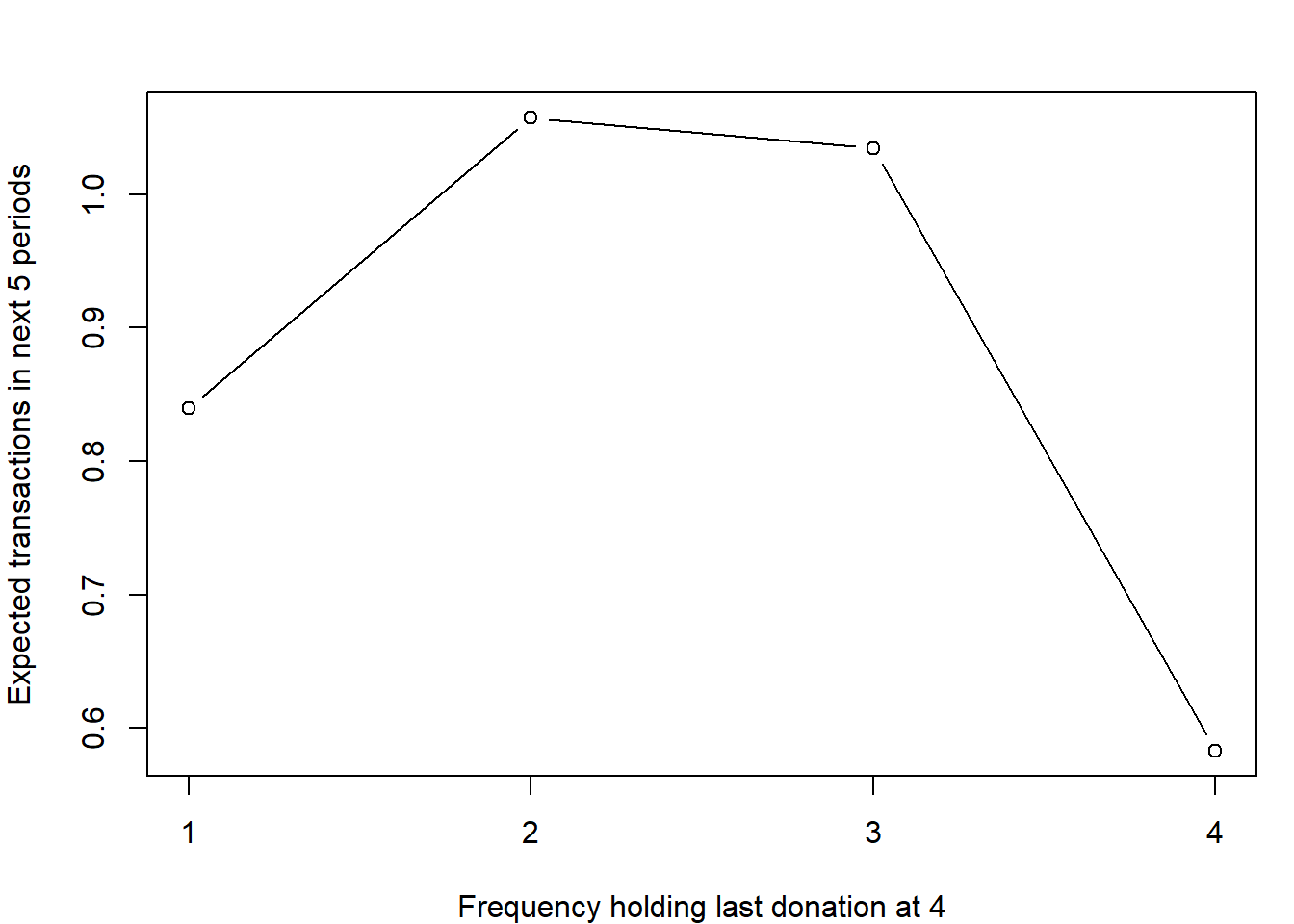
What’s interesting about this curve is that customer with the largest frequency is not the one with the highest future predicted purchases. This is something known as the increasing frequency paradox. Why? The likelihood that he or she is still alive decreases in \(x\).

par(mfrow=c(1,1))
par(mai=c(.8,.8,.5,.2))

plot(bgbb.PAlive(params, x=1:4, t.x=4, n.cal=6), ylab ="Probability that customer is alive next period", xlab="Frequency holding last donation at 4", ylim=c(0,1), type="b", xaxt="n")
xtick<-seq(1, 4, by=1)
axis(side=1, at=xtick, labels = TRUE)

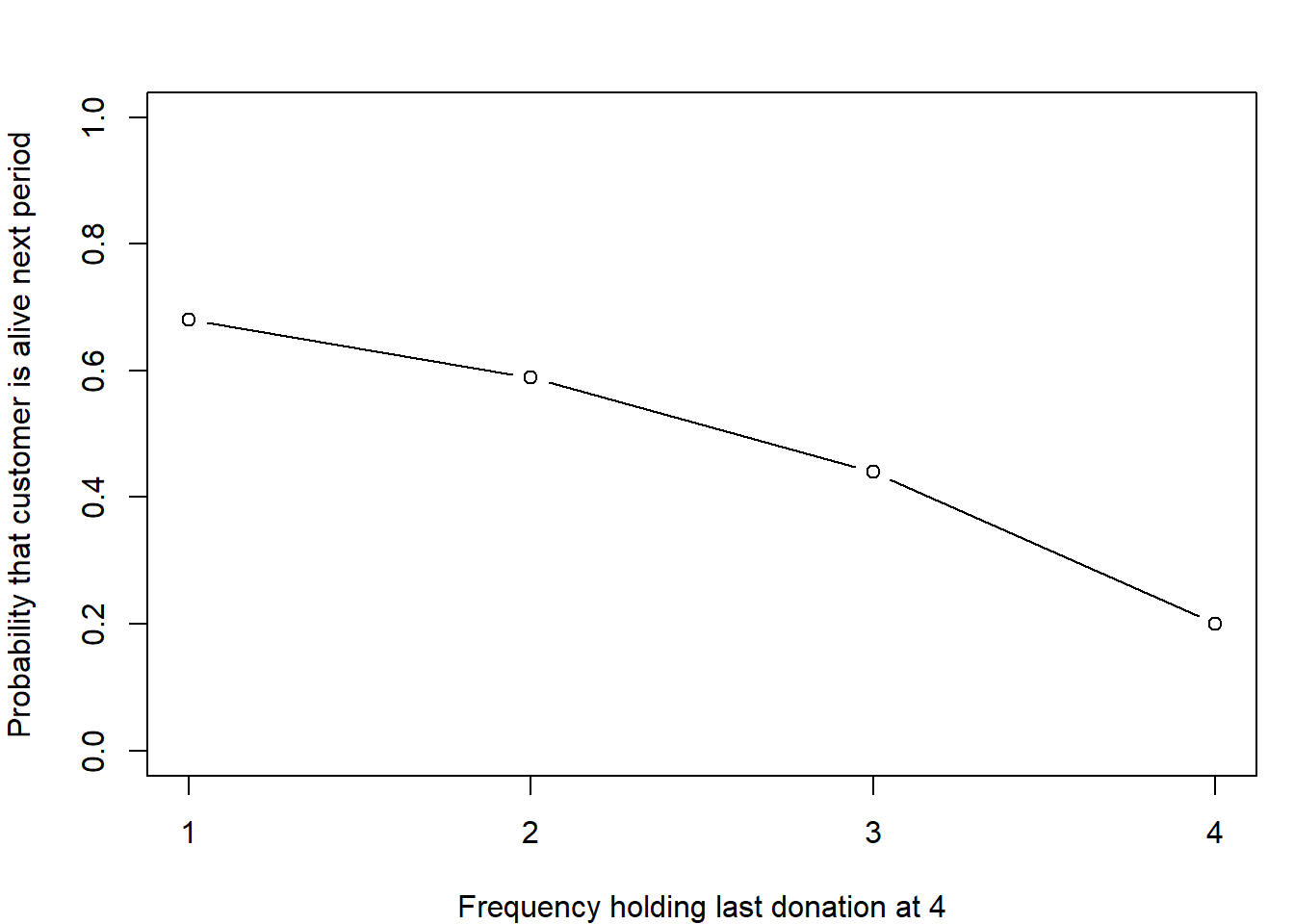
On the one hand, higher \(x\) means a higher \(p\) which means more expected transactions in the future. On the other hand, if the last two periods were no purchases, a higher \(x\) means that \(P(alive)\) is lower. This second effect is stronger than the first effect, resulting in a lower expectations when \(x=4\) compared to when \(x=2,3\).

CLV

Given model assumptions 2 and 3, we know that the probability of making a purchase is equal to the probability that a customer is alive times the probability of making a purchase conditional on being alive: \[ P(\, Y(t) = 1 \mid p, \theta) = p \, (1-\theta)^t \] We integrate \(p\) and \(\theta\) over their mixing distributions to get the proability for a randomly chosen customer: \[ \begin{array}{ccl} P(\, Y(t) = 1 \mid \alpha, \beta, \gamma, \delta) &=& \displaystyle \int_0^1 \int_0^1 P(\, Y(t) = 1 \mid p, \theta) \, f(p \; | \; \alpha,\beta) \, f(\theta \; | \; \gamma,\delta) \, dp \, d\theta \\ &=& \displaystyle \left(\frac{\alpha}{\alpha+\beta}\right) \frac{B(\gamma, \delta+t)}{B(\gamma, \delta)} \end{array} \]

CLV is then the discounted sum of the probability of making a transaction times some average amount per transaction (\(m\)):

\[ \begin{array}{ccl} E[CLV] & = & m \; \left( 1 + \sum_{t=1}^{\infty} P(\, Y(t) = 1 \mid \alpha, \beta, \gamma, \delta) \frac{1}{(1+d)^t} \right) \\ & = & m \; \times \textrm{DET} \end{array} \]

DET means Discounted Expected Transactions. For implementing this in R, we have to choose some upper bound to the sum, i.e. \(T=200\).

BGBBCLV<-function(params,m,d,T) {
params<-unname(params)
al<-params[1]
be<-params[2]
ga<-params[3]
de<-params[4]
DET<-1   # at time zero there has to be a purchase
for (i in 1:T) {
    DET<-DET+(al/(al+be))*(beta(ga,de+i)/beta(ga,de))*1/(1+d)^{i}
}
CLV=m*DET  # convert discount expected purchases into expected value
return(CLV)    #return the CLV
}

CLV <- BGBBCLV(params = params, m=50,d=.1,T=200)

CLV for a random customer with parameters as esimated, \(m=€50, d=.1, T=200\) is €185.

RLV

Lastly we can calculate the residual lifetime value of a donor with history \((x,t_x,n)\). The residual lifetime value is the present value of the expected future transaction stream standing at time \(t\). \[ \begin{array}{ccl} E[RLV] & = & \displaystyle m \; \left ( P(\textrm{alive at} \, n) \; \sum_{t=n+1}^{\infty} \; P(Y_t = 1 \mid \textrm{alive at} \, t) \frac{P(\textrm{alive at} \, t \mid t>n)}{(1+d)^{t-n}} \right)\\ & = & \displaystyle m \times \textrm{DERT} \end{array} \]

DERT means Discounted expected residual transactions. Here is what it looks like for our sample:

m <- 50
DERT <- bgbb.rf.matrix.DERT(params, donationsSummary$rf.matrix, d=0.1)
RLV <- m*DERT
RLV_mat <- cbind(Alive_mat,DERT, RLV)
RLV_mat <- data.frame(RLV_mat)
kable(RLV_mat, format="pipe")

x	t.x	n.cal	custs	PAlive	DERT	RLV
6	6	6	1203	0.930	5.910	295.48
5	6	6	728	0.930	5.089	254.46
4	6	6	512	0.930	4.269	213.44
3	6	6	357	0.930	3.448	172.42
2	6	6	234	0.930	2.628	131.40
1	6	6	129	0.930	1.808	90.38
5	5	6	335	0.522	2.855	142.74
4	5	6	284	0.697	3.197	159.84
3	5	6	225	0.767	2.842	142.10
2	5	6	173	0.805	2.272	113.62
1	5	6	119	0.828	1.609	80.44
4	4	6	240	0.200	0.918	45.92
3	4	6	181	0.440	1.629	81.46
2	4	6	155	0.590	1.665	83.27
1	4	6	78	0.680	1.322	66.09
3	3	6	322	0.095	0.352	17.60
2	3	6	255	0.299	0.844	42.21
1	3	6	129	0.481	0.935	46.76
2	2	6	613	0.066	0.188	9.38
1	2	6	277	0.255	0.495	24.74
1	1	6	1091	0.069	0.135	6.75
0	0	6	3464	0.108	0.115	5.74

maxround=round(max(RLV),-2)
RLV_mat$RLV[1] 

## [1] 295

with(RLV_mat, hist(rep(x = RLV_mat$RLV, times = RLV_mat$custs), xaxt='n', xlim = c(0,maxround), xlab = "RLV ($)", ylab="frequency", main="Histogram of Residual Lifetime Value (RLV)"))
axis(side=1, at=seq(0,maxround, 50), labels=seq(0,maxround, 50))

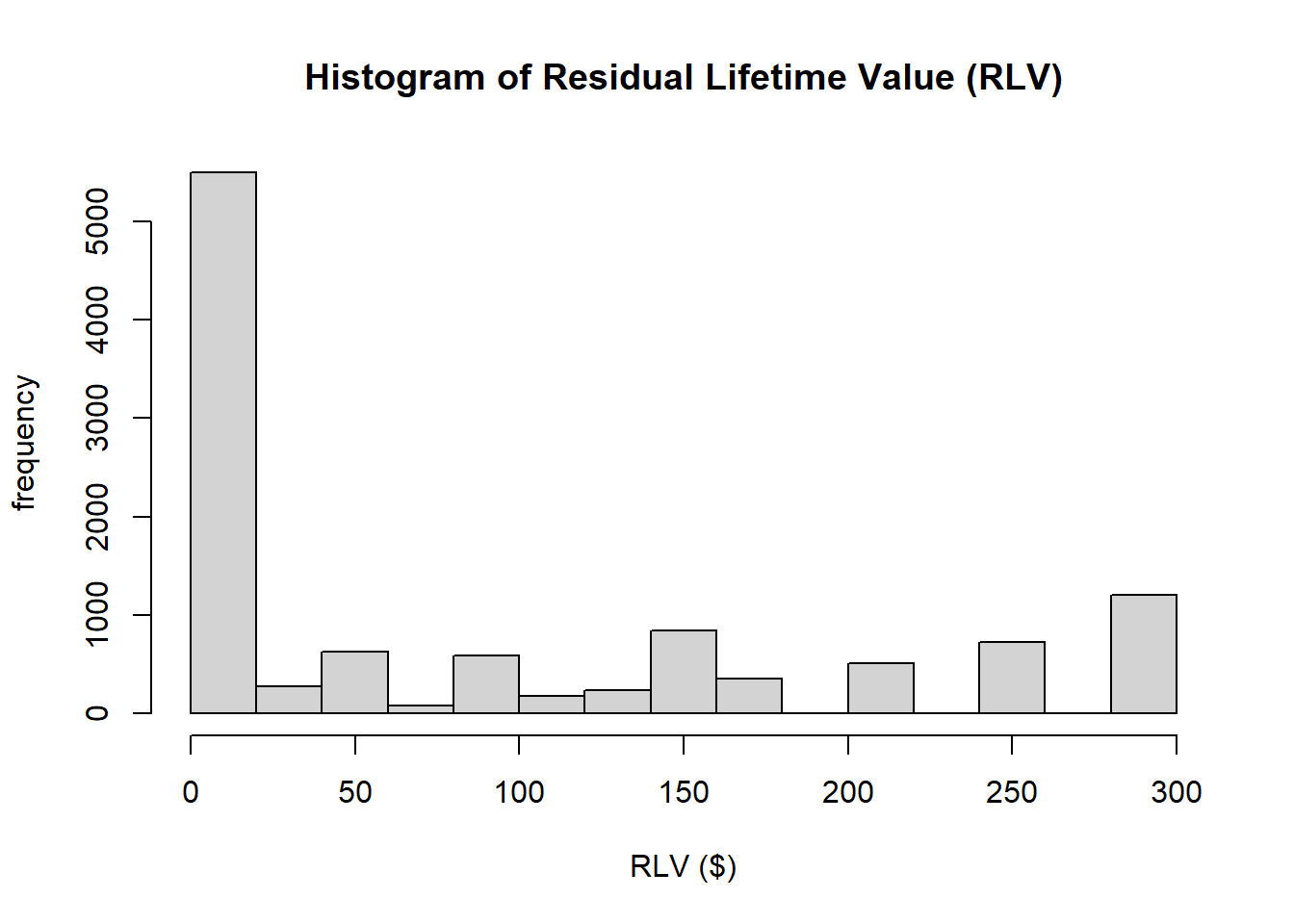
If we assume \(m=50\) is the value of a donation and we use a yearly discount rate of \(d=0.1\), the RLV of a customer who makes “6 for 6” repeat donations is €295.48.

---

1. Schmittlein, D., Morrison, D., & Colombo, R. (1987). Counting Your Customers: Who Are They and What Will They Do Next? Management Science, 33(1), 1-24.↩︎

2. Fader, Peter S., Bruce G.S. Hardie, and Jen Shang. “Customer-Base Analysis in a Discrete-Time Noncontractual Setting.” Marketing Science, 29(6), pp. 1086-1108. 2010. INFORMS. link↩︎

3. It’s not shifted because 0 is a valid outcome.↩︎