Quiz 1: Test & Roll

Question 1

A company is considering whether to do a test on its marketing campaign. Direct marketing costs €2.00 to send. The company sells a product for €50 and 34% of that remains after taking costs and other items into account.

What’s the breakeven response rate threshold, i.e., the response probability this company needs for its mailing to be profitable?

\[ \pi\hat{p}-c>0 \]

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

m <- 50*0.34
c <- 2
brk <- c/m

## Breakeven Response Rate Threshold: 0.118

Question 2

A company is considering whether to do a test on its marketing campaign. Direct marketing costs €2.00 to send. The company sells a product for €50 and 34% of that remains after taking costs and other items into account.

Using the ebeer data set, estimate the response rate.

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

The data:

ebeer <- read_sav("C:/Users/danny/OneDrive/Análisis Cuantitativo y Econometría/Marketing Analytics/Customer Analytics/Quizes/1 Uncertainty/E-Beer.sav")

# Eliminate NA's
ebeer <- ebeer[!is.na(ebeer$respmail),]
# Response is numeric and 0/1
ebeer$respmail <- as.numeric(ebeer$respmail)

Response Rate:

p_hat <- round(mean(ebeer$respmail, na.rm=TRUE),3)
p_hat_se <- sqrt(p_hat*(1-p_hat)/nrow(ebeer))

## The mean response rate is 0.124 and it's standard deviation is 0.005

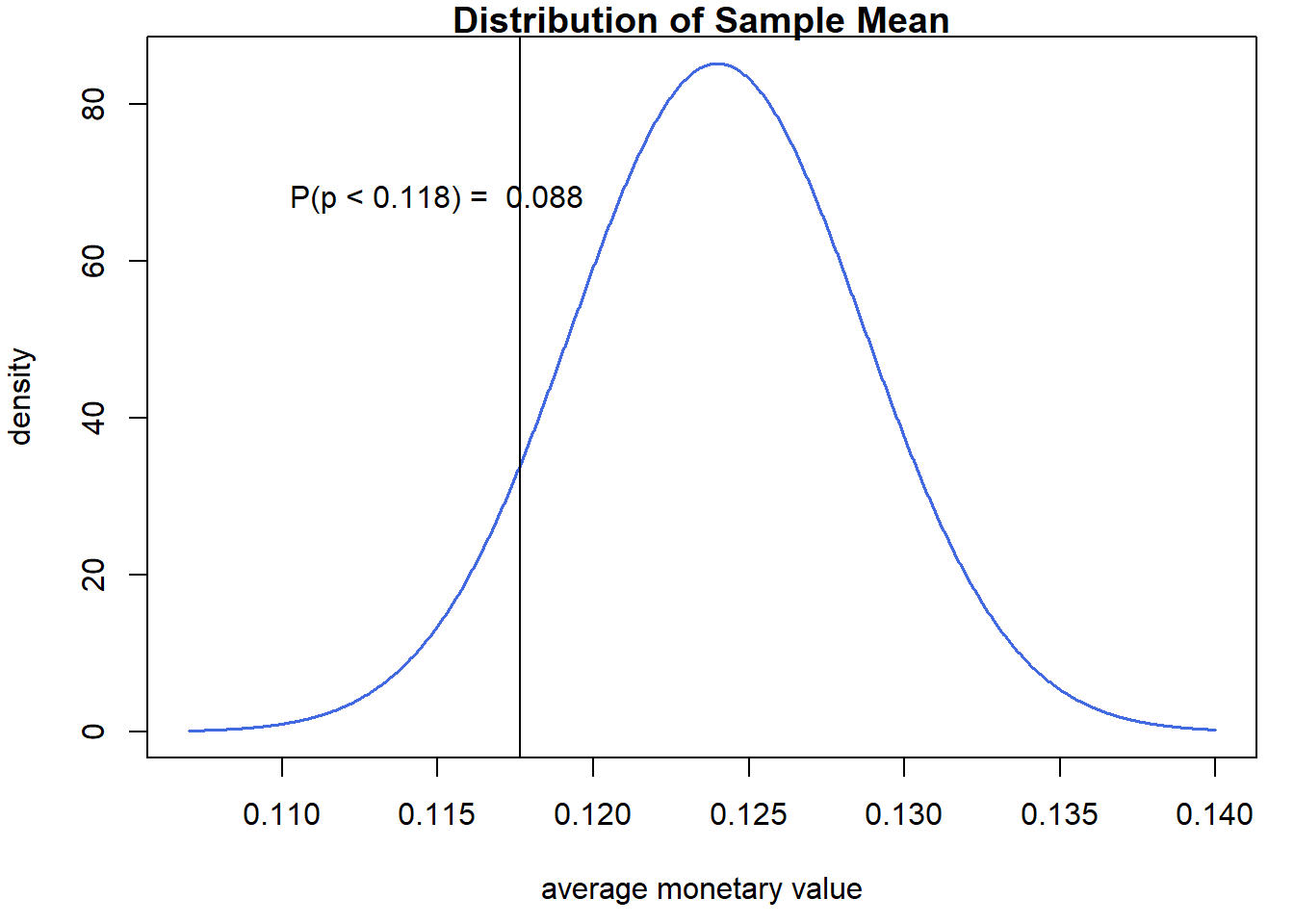
Assuming a normal distribution, we can estimate the probability that our estimated response rate is below the breakeven point:

B <- 10000
set.seed(19103)
post_draws <- rnorm(B, mean = p_hat, sd = p_hat_se) # random deviates
prob <- sum(post_draws<brk)/B

## The probability of being below the breakeven point is 0.088

We can plot these results:

xx <- seq(.107,.14,length=1000)

par(mai=c(.9,.8,.2,.2))
plot(xx, dnorm(xx, p_hat, p_hat_se), main="Distribution of Sample Mean", 
     type="l", col="royalblue", lwd=1.5,
     xlab="average monetary value", ylab="density")
abline(v=brk)
text(x = .115,y= 68, paste("P(p < 0.118) = ", round(prob,3) ))

Question 3

A company is considering whether to do a test on its marketing campaign. Direct marketing costs €2.00 to send. The company sells a product for €50 and 34% of that remains after taking costs and other items into account.

If they decide to roll it out to the population, what’s the probability that we make a mistake, i.e., the true response rate is lower than the breakeven response rate? Use a bootstrap with the same seed and number of draws we did in the R notebook. 

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

The bootstrap code:

B <- 10000 
mub <- c() 
set.seed(19103)
for (b in 1:B){
  samp_b = sample.int(nrow(ebeer), replace=TRUE) 
  mub <- c(mub, mean(ebeer$respmail[samp_b])) # RESPONSE RATE
}

Probability that True Response Rate is lower than Breakeven Response Rate:

B <- 10000
set.seed(19103)
post_draws <- rnorm(B,mean(mub),sd(mub)) # random deviates
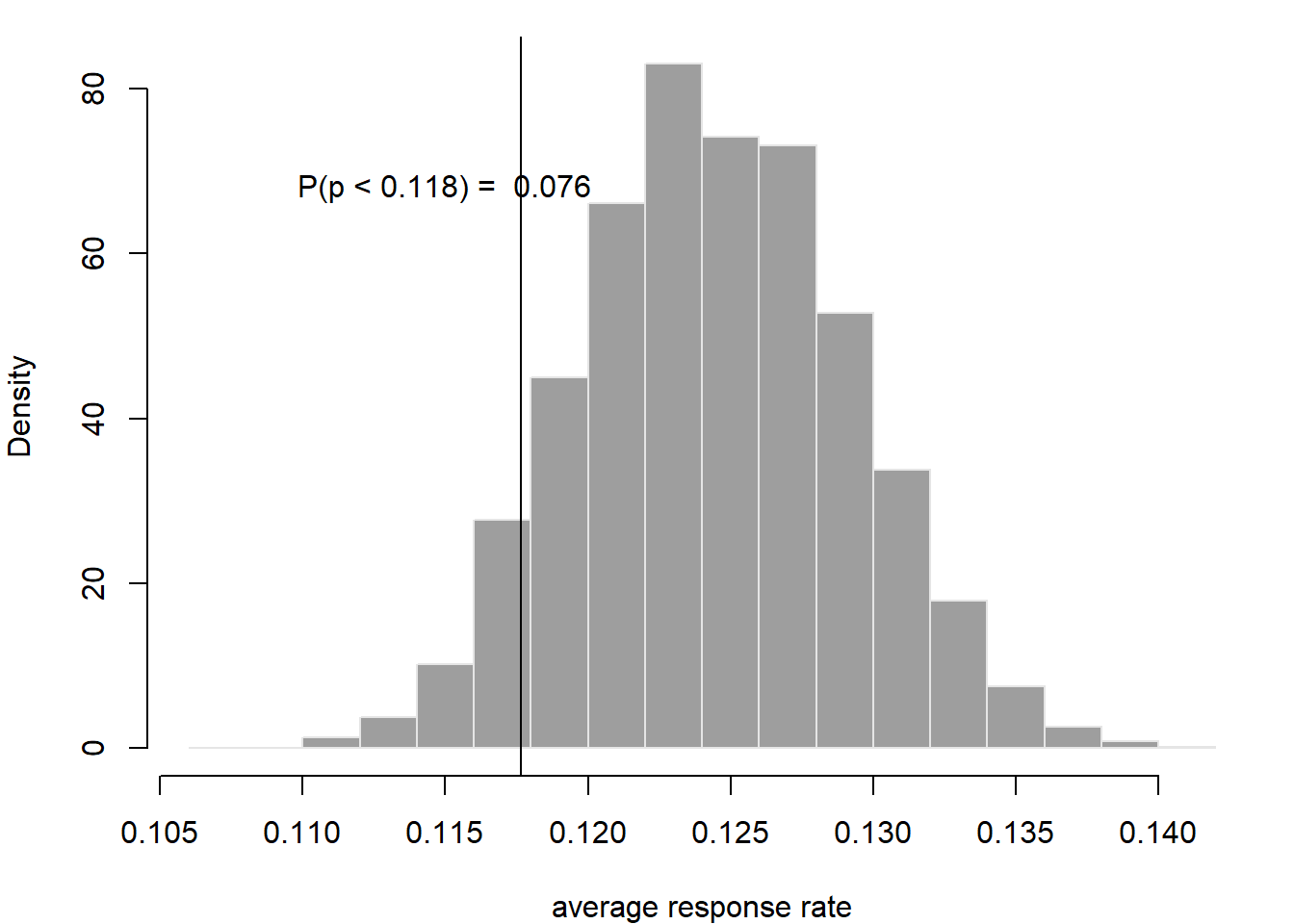
prob <- round(sum(post_draws<brk)/B, 3)

## The probability of being below the breakeven point is 0.076

We can plot this:

xx <- seq(.11,.14,length=1000)

par(mai=c(.8,.8,.2,.2))
hist(mub, main="", xlab="average response rate",
     col=8, border="grey90", freq=FALSE)
abline(v=brk)
text(x = .115,y= 68, paste("P(p < 0.118) = ", round(prob,3) ))

Question 4

A company wants to calculate the value of testing. They have a margin of 25, a marketing cost of 0.40, and a total customer base of 50000. Their sample is 5000 customers. In the past, campaigns have either been a success, with a response rate of .05, or a failure, with a response rate of 0.001. Historically, 80% of past mailings have been a failure.

Would the company decide to send without a test?

Our data:

m <- 25
c <- 0.40
N <- 50000
n <- 5000

p_s <- 0.05  # with P(Success)=0.2
p_f <- 0.001 # with P(Failure)=0.8

Option Value (Without Test):

(0.2)*N*(p_s*m-c)+(0.8)*N*(p_f*m-c)

## [1] -6500

Question 5

A company wants to calculate the value of testing. They have a margin of 25, a marketing cost of 0.40, and a total customer base of 50000. Their sample is 5000 customers. In the past, campaigns have either been a success, with a response rate of .05, or a failure, with a response rate of 0.001. Historically, 80% of past mailings have been a failure.

What is the profit if the company tests and it is a failure?

Option Value (Failure Case Only):

n*(p_f*m-c)

## [1] -1875

Question 6

A company wants to calculate the value of testing. They have a margin of 25, a marketing cost of 0.40, and a total customer base of 50000. Their sample is 5000 customers. In the past, campaigns have either been a success, with a response rate of .05, or a failure, with a response rate of 0.001. Historically, 80% of past mailings have been a failure.

What’s the expected profit with a test?

Option Value (Total Expected):

cat("$",(0.2)*N*(p_s*m-c)+(0.8)*n*(p_f*m-c))

## $ 7000

Question 7

A company wants to calculate the value of testing. They have a margin of 25, a marketing cost of 0.40, and a total customer base of 50000. Their sample is 5000 customers. In the past, campaigns have either been a success, with a response rate of .05, or a failure, with a response rate of 0.001.  Historically, 80% of past mailings have been a failure.

If running a test costs 5000, should the company do it?

(0.2)*N*(p_s*m-c) + (0.8)*(n*(p_f*m-c)) - 5000

## [1] 2000