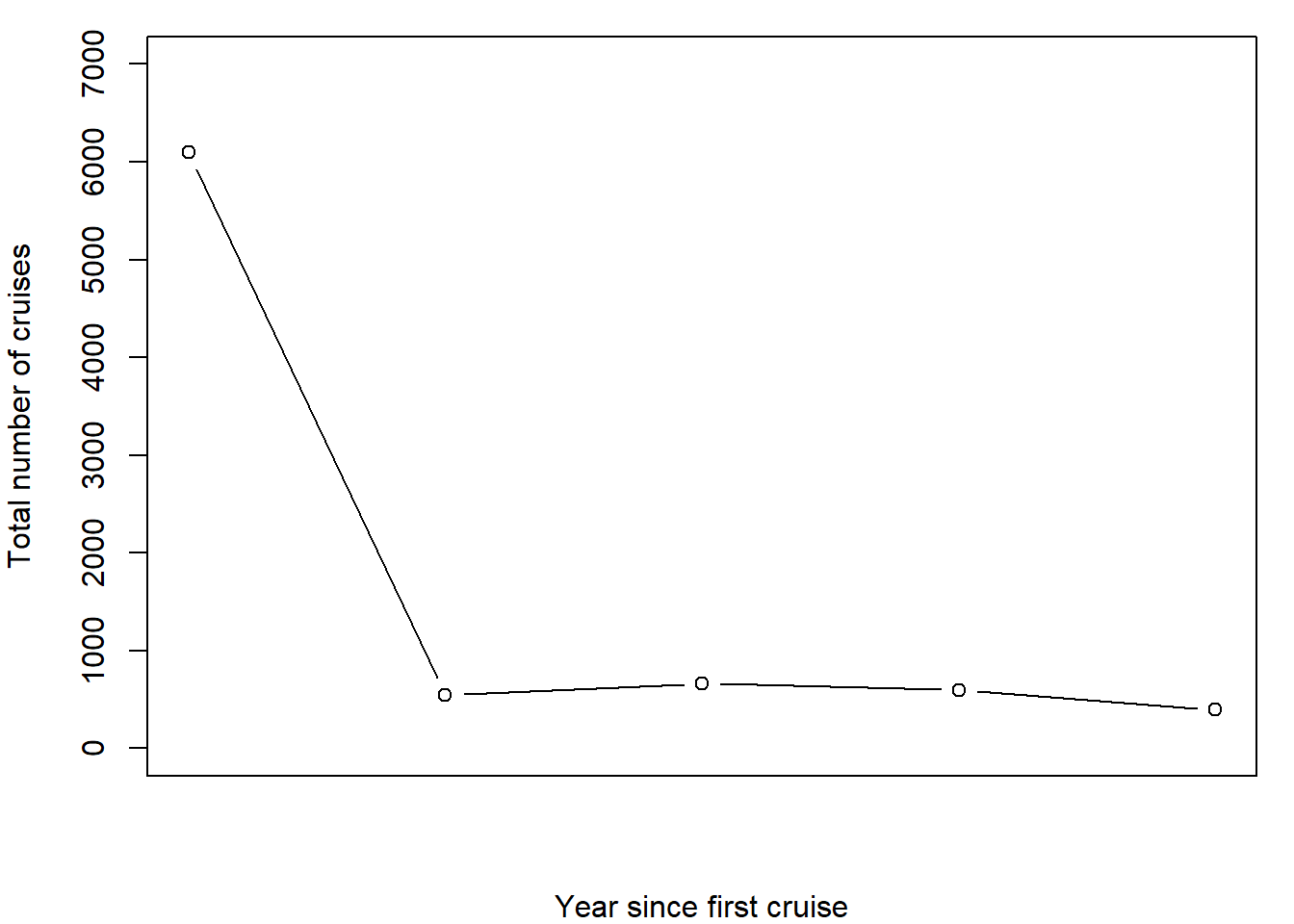A cruise-ship company characterizes customer behavior in terms of
whether or not each customer went on a cruise in 2000, 2001, 2002, etc.
This data is from Berger et al. (2003). There were 6,094 customers who
made their first cruise in year 0. We follow their repeat cruises for
the following 4 years: we record simply whether in a given year a
customer went on a repeat cruise or not.
There’s not enough data to do a proper holdout sample, so everything
will be used in the estimation sample.
cal.rf.matrix <- read.csv("rf_cruise.csv", sep = ";")
trans<-read.csv("annual_cruises.csv")
Question 1
It’s instructive to see how the data used to estimate the model were
calculated from the original data set.
Go to the original paper and look at Figure 1 and the accompanying
text. Ignore t, the number of trips; focus on the “p” and “no”
numbers. Verify that the number of “4 for 4” customers in the flow
chart is the same as in cal.rf.matrix.
What are the distinct paths (e.g., 0100 means no cruise in
year 1, cruise in year 2, no cruise in year 3, etc) in the diagram that
comprises the (x=2, t_x=4, n=4) cell in cal.rf.Matrix?
Give them in terms of 4 binary digits (0000 means no repeat
cruises in any of the four years)
trans <- trans$x
tt <- seq(0, length(trans)-1, by=1)
par(mfrow=c(1,1))
par(mai=c(.8,.8,.2,.2))
plot(tt,trans, type="b", ylab="Total number of cruises", xlab="Year since first cruise", main="", xaxt='n', ylim = c(0,7000))
Question 2
Estimate the BG/BB parameters, using (1,1,1,1) as starting
parameters.
Provide your answer with two decimals separated by a dot, not a
comma (e.g. 0.12).
Initial Parameters:
par.start <- c(1, 1, 1, 1)
rf.matrix <- cal.rf.matrix
BGBB Estimation:
params <- bgbb.EstimateParameters(rf.matrix, par.start)
round(params,2)
## [1] 0.66 5.19 92.13 1000.00
Log-Likelihood:
LL <- bgbb.rf.matrix.LL(params, rf.matrix)
LL
## [1] -7131
Question 3
What happens if you restrict the max parameter value to be
100? You can do this by using the option max.param.value = . What are
the parameter values?
Provide your answer with two decimals separated by a dot, not a
comma (e.g. 0.12).
params <- bgbb.EstimateParameters(rf.matrix, par.start, max.param.value = 100)
round(params, 2)
## [1] 0.66 5.20 9.34 100.00
Question 4
Does the log likelihood rounded to a whole number change
using estimates from Q2 and Q3?
Likelihood:
LL <- bgbb.rf.matrix.LL(params, rf.matrix)
LL
## [1] -7131
Question 5
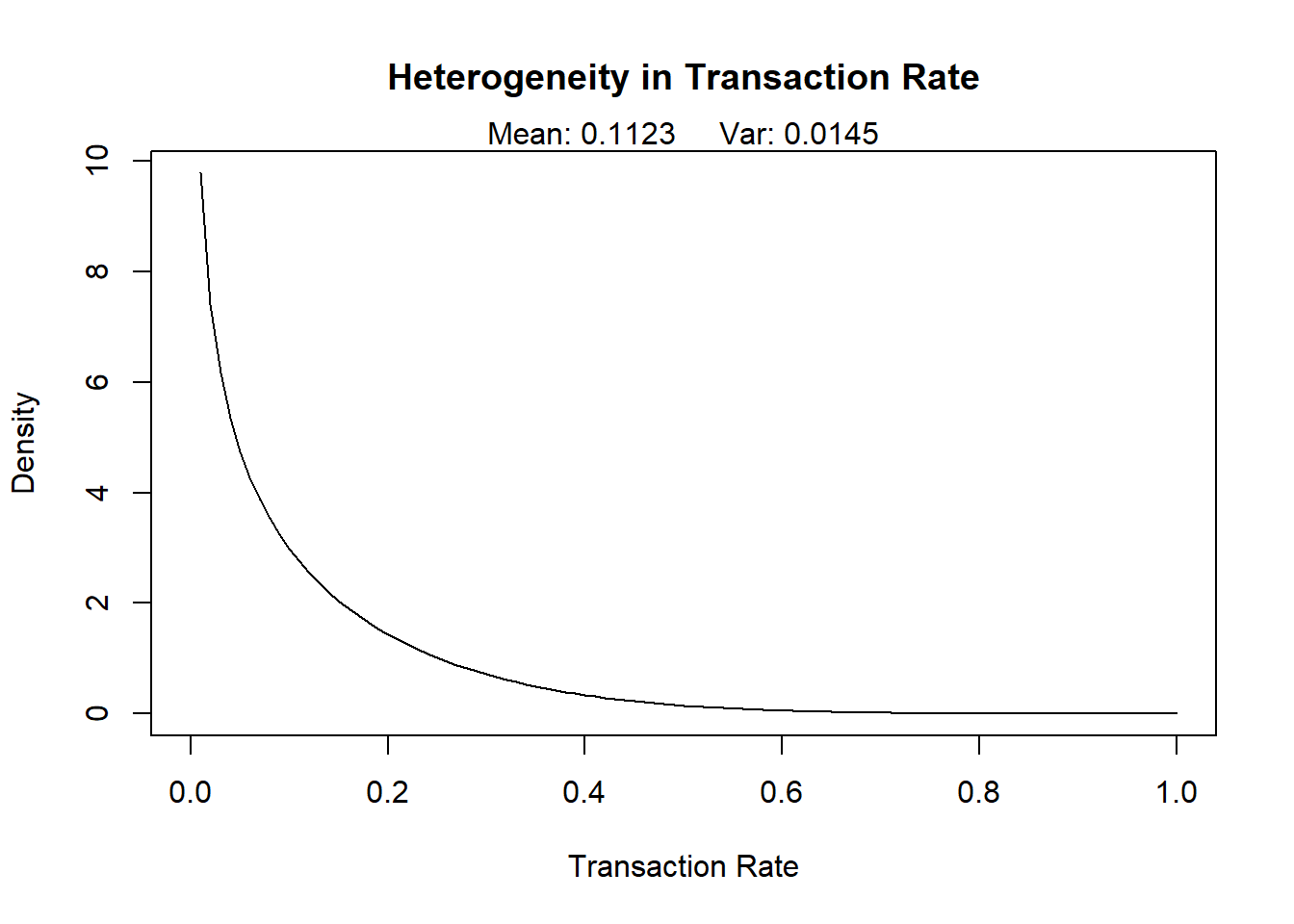
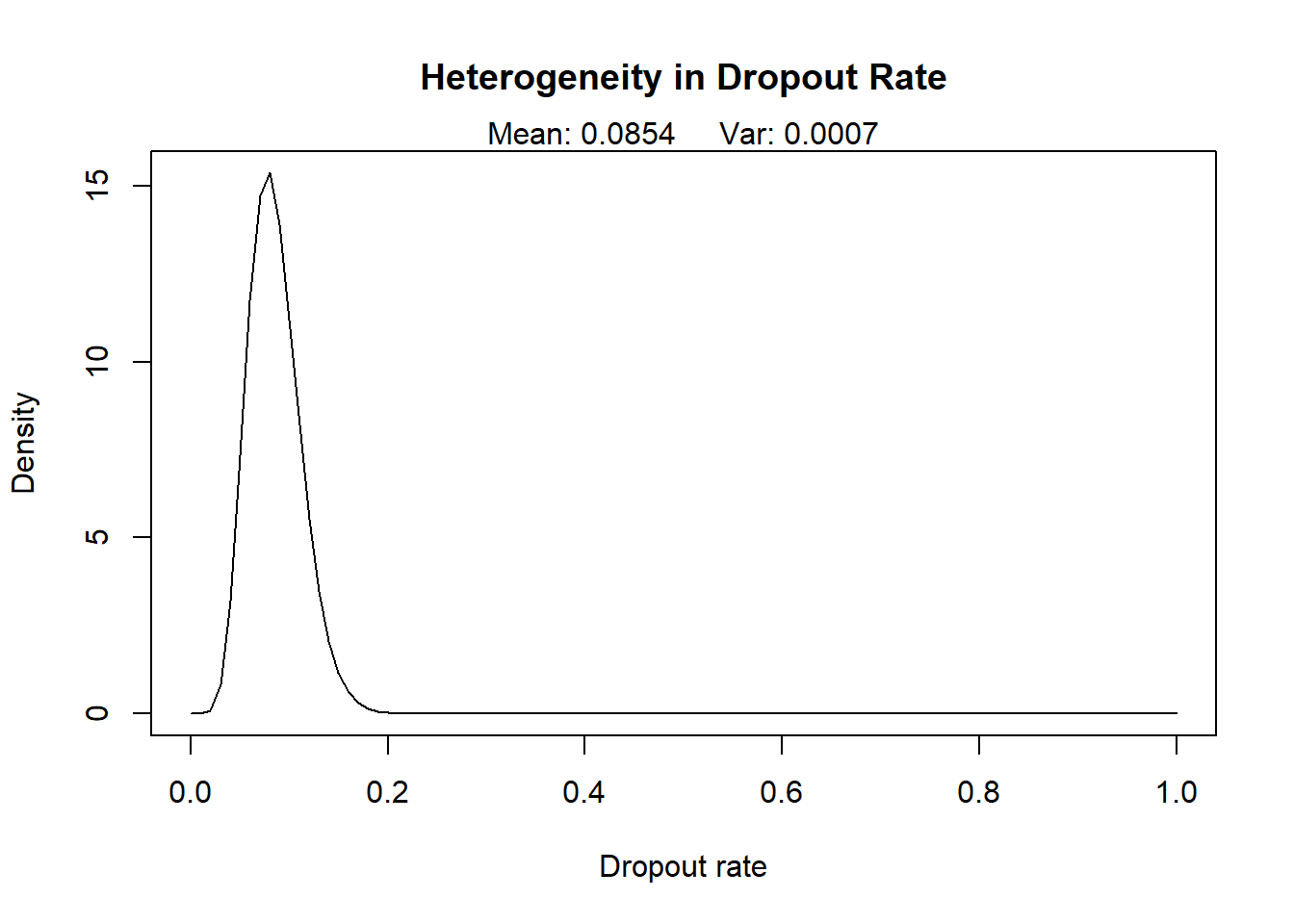
Graph out the distributions of the transaction rate and
dropout rate for both sets of estimates from Q2 and Q3. In both cases,
which distribution varies the least in the population?
Transaction Rate, while alive:
temp <- bgbb.PlotTransactionRateHeterogeneity(params)
Drop Out Rate:
temp <- bgbb.PlotDropoutRateHeterogeneity(params)
Mean of Rates:
par(mfrow=c(1,2))
par(mai=c(.8,.8,.5,.2))
temp<-bgbb.PlotTransactionRateHeterogeneity(params)
par(mai=c(.8,.8,.5,.2))
temp<-bgbb.PlotDropoutRateHeterogeneity(params)
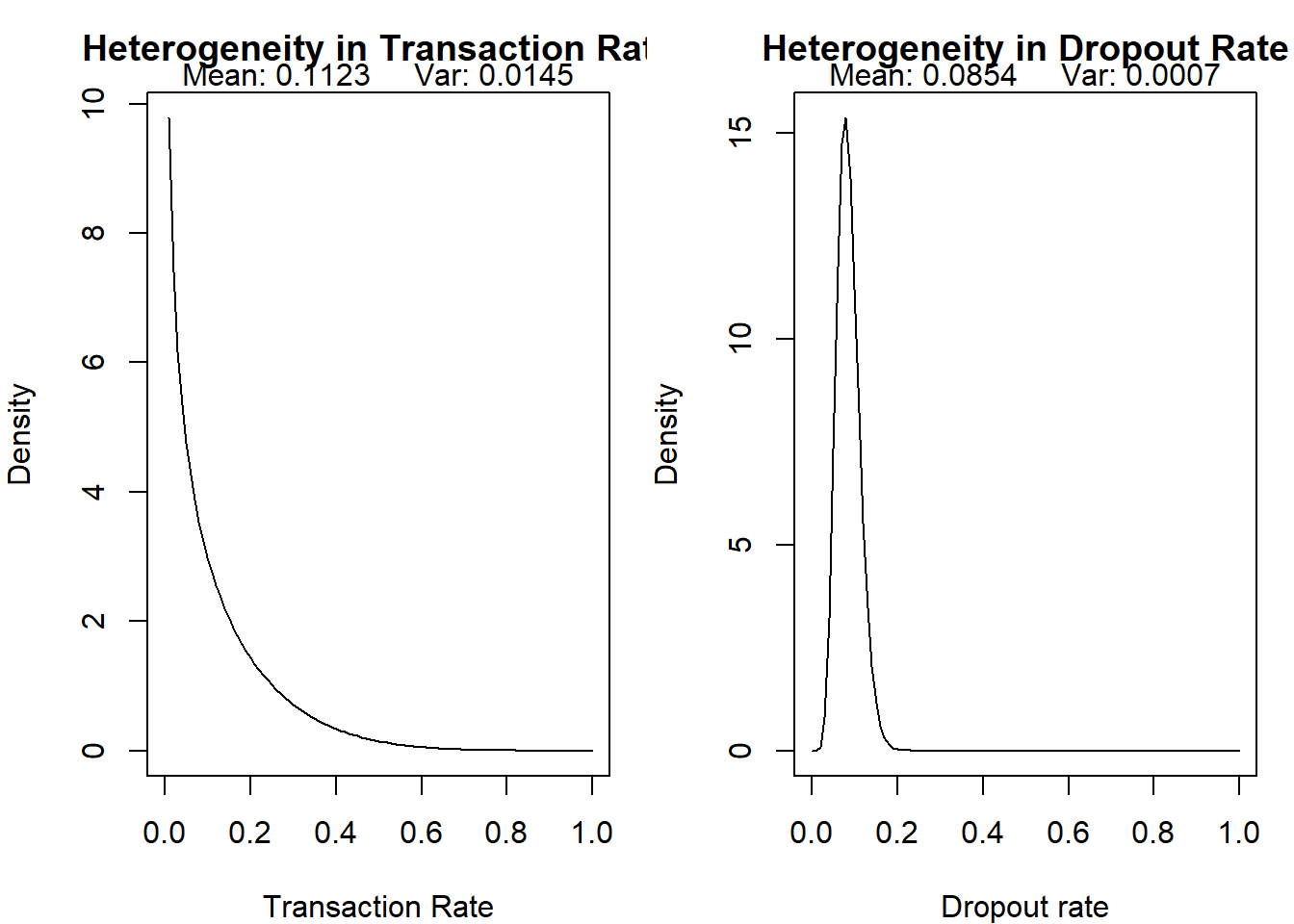
## avg trans rate = 0.11
## avg dropout rate = 0.09
Question 6
In the 4th year after the first purchase, how many
actual repeat cruises were there, and how many are predicted by the BGBB
model (using Q2 estimates)?
Provide your answer with zero decimals (e.g. 120 or
-120).
pred <- bgbb.PlotTrackingInc(params, rf.matrix, trans[2:5], xticklab = seq(1,4))
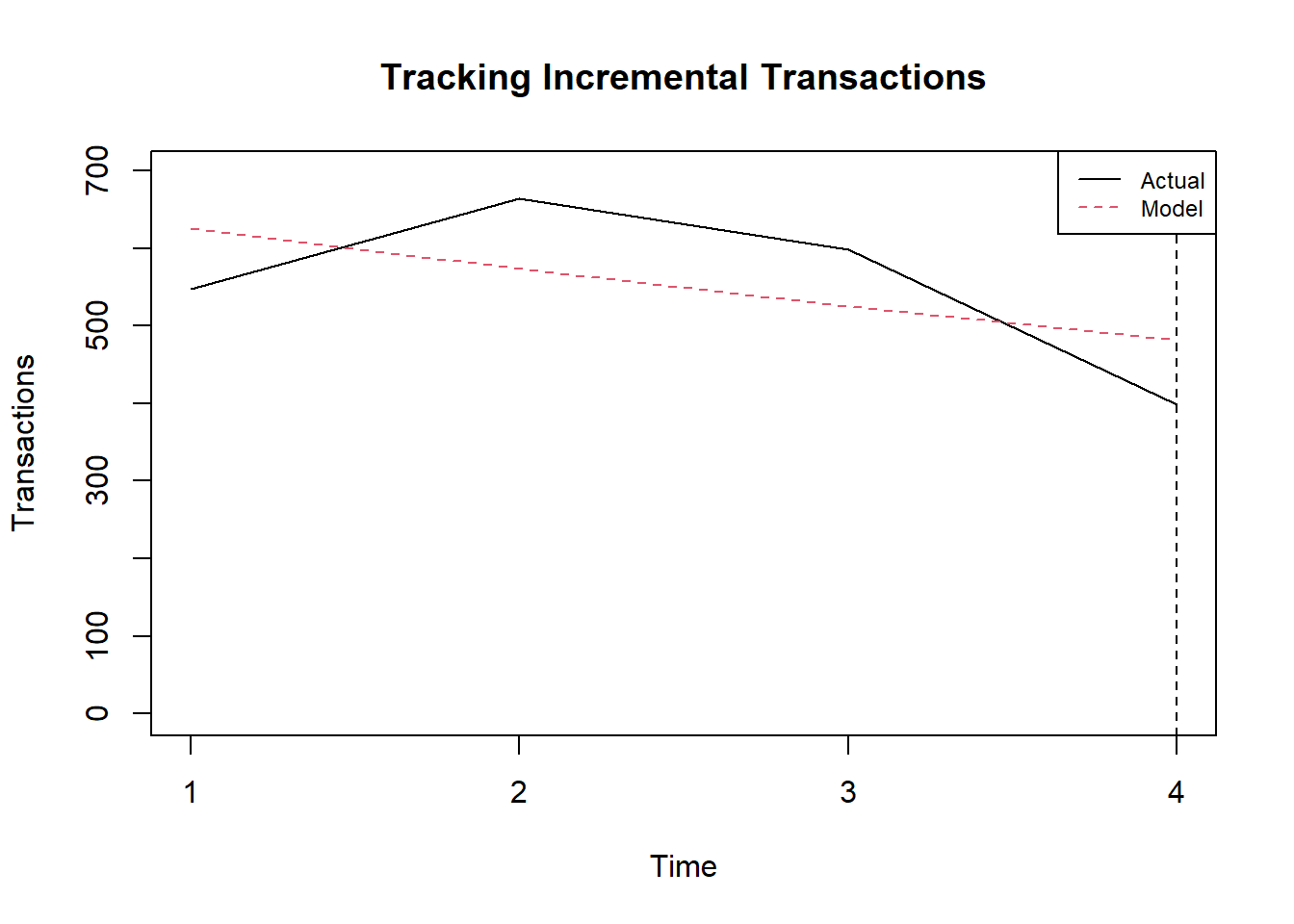
pred
## [,1] [,2] [,3] [,4]
## actual 548 664 598 398
## expected 626 573 525 481
## predicted = 481
## actual = 398
Question 7
According to the model, what is the predicted number of
cruises in the next 4 years for someone who took a cruise every year so
far (using Q2 estimates)?
Provide your answer with two decimals separated by a dot, not a
comma (e.g. 0.12).
Individual-Level Prediction:
comp <- bgbb.HeatmapHoldoutExpectedTrans(params, n.cal=4, n.star=4)
## layout: widths = 0.05 4 , heights = 0.25 4 ; lmat=
## [,1] [,2]
## [1,] 0 3
## [2,] 2 1
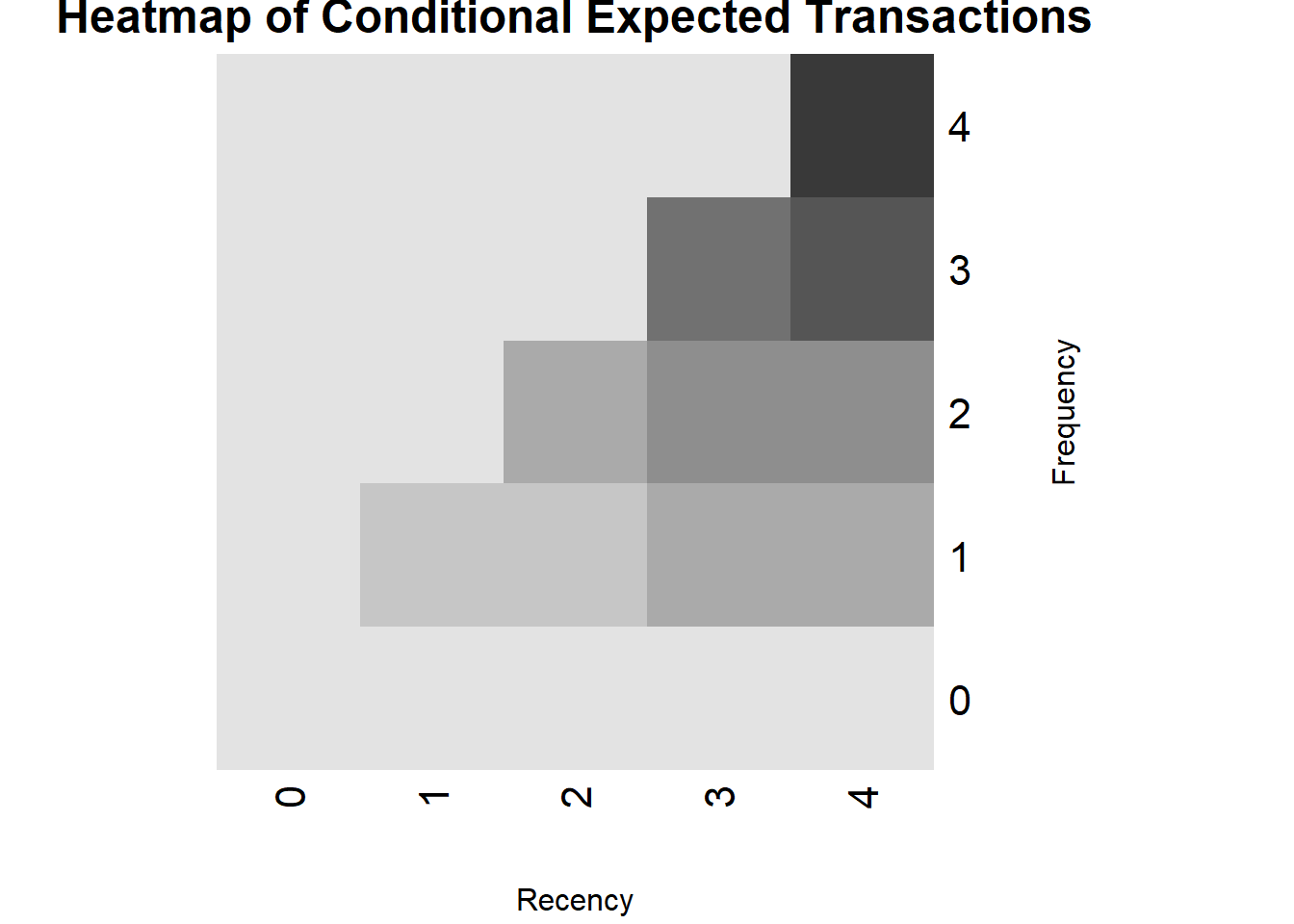
comp
## 0 1 2 3 4
## 0 0.141 0.000 0.000 0.000 0.000
## 1 0.000 0.366 0.431 0.491 0.546
## 2 0.000 0.000 0.651 0.775 0.875
## 3 0.000 0.000 0.000 1.043 1.205
## 4 0.000 0.000 0.000 0.000 1.534
Someone who took a cruise every year (F=4) so far (R=4, period of
last purchase)
round(comp[5,5],2)
## [1] 1.53
Question 8
What is the RLV for someone who has taken a cruise every year
so far (F=R=4), assuming each cruise yields on average $600 in profit,
and the discount rate is 0.1 (using Q3 estimates)?
Provide your answer with zero decimals, without the dollar sign
(e.g. 120 or -120).
First, we need CLV:
m <- 600
BGBBCLV<-function(params,m,d,T) {
params<-unname(params)
al<-params[1]
be<-params[2]
ga<-params[3]
de<-params[4]
DET<-1
for (i in 1:T) {
DET<-DET+(al/(al+be))*(beta(ga,de+i)/beta(ga,de))*1/(1+d)^{i}
}
CLV=m*DET
return(CLV)
}
CLV <- BGBBCLV(params = params, m=600,d=.1,T=200)
CLV
## [1] 941
Now we can get RLV:
m <- 600
DERT <- bgbb.rf.matrix.DERT(params, rf.matrix = cal.rf.matrix, d=0.1)
RLV <- m*DERT
RLVmatrix <- cbind(cal.rf.matrix,round(RLV))
RLVmatrix
## x t.x n.cal custs round(RLV)
## 1 4 4 4 18 1459
## 2 3 4 4 66 1146
## 3 2 4 4 98 833
## 4 1 4 4 216 519
## 5 3 3 4 34 993
## 6 2 3 4 180 737
## 7 1 3 4 292 467
## 8 2 2 4 64 619
## 9 1 2 4 342 410
## 10 1 1 4 302 348
## 11 0 0 4 4482 134
## Q6 RLV for 4 for 4 = $ 1459
LS0tDQp0aXRsZTogIkFzc2lnbm1lbnQgNzogQ0xWIC0gTm9uLWNvbnRyYWN0dWFsIHNldHRpbmdzIg0KYXV0aG9yOiAiRGFuaWVsIFJlZGVsIg0KZGF0ZTogIjIwMjMtMDEtMjYiDQpvdXRwdXQ6IA0KICBodG1sX2RvY3VtZW50Og0KICAgIHRvYzogVFJVRQ0KICAgIHRvY19mbG9hdDogVFJVRQ0KICAgIGNvZGVfZG93bmxvYWQ6IFRSVUUNCi0tLQ0KDQpgYGB7ciBzZXR1cCwgaW5jbHVkZT1GQUxTRX0NCmtuaXRyOjpvcHRzX2NodW5rJHNldChlY2hvID0gVFJVRSkNCm9wdGlvbnMoInNjaXBlbiI9MTAwLCAiZGlnaXRzIj0zLCB3aWR0aCA9IDMwMCkNCnJtKGxpc3Q9bHMoKSkNCmxpYnJhcnkocmVhZHIpDQpsaWJyYXJ5KCJCVFlEIikNCmBgYA0KDQpBIGNydWlzZS1zaGlwIGNvbXBhbnkgY2hhcmFjdGVyaXplcyBjdXN0b21lciBiZWhhdmlvciBpbiB0ZXJtcyBvZiB3aGV0aGVyIG9yIG5vdCBlYWNoIGN1c3RvbWVyIHdlbnQgb24gYSBjcnVpc2UgaW4gMjAwMCwgMjAwMSwgMjAwMiwgZXRjLiBUaGlzIGRhdGEgaXMgZnJvbSBCZXJnZXIgZXQgYWwuICgyMDAzKS7CoCBUaGVyZSB3ZXJlIDYsMDk0IGN1c3RvbWVycyB3aG8gbWFkZSB0aGVpciBmaXJzdCBjcnVpc2UgaW4geWVhciAwLsKgIFdlIGZvbGxvdyB0aGVpciByZXBlYXQgY3J1aXNlcyBmb3IgdGhlIGZvbGxvd2luZyA0IHllYXJzOiB3ZSByZWNvcmQgc2ltcGx5IHdoZXRoZXIgaW4gYSBnaXZlbiB5ZWFyIGEgY3VzdG9tZXIgd2VudCBvbiBhIHJlcGVhdCBjcnVpc2Ugb3Igbm90LsKgDQoNClRoZXJlJ3Mgbm90IGVub3VnaCBkYXRhIHRvIGRvIGEgcHJvcGVyIGhvbGRvdXQgc2FtcGxlLCBzbyBldmVyeXRoaW5nIHdpbGwgYmUgdXNlZCBpbiB0aGUgZXN0aW1hdGlvbiBzYW1wbGUuDQoNCmBgYHtyfQ0KY2FsLnJmLm1hdHJpeCA8LSByZWFkLmNzdigicmZfY3J1aXNlLmNzdiIsIHNlcCA9ICI7IikNCnRyYW5zPC1yZWFkLmNzdigiYW5udWFsX2NydWlzZXMuY3N2IikNCmBgYA0KDQojIFF1ZXN0aW9uIDENCg0KSXQncyBpbnN0cnVjdGl2ZSB0byBzZWUgaG93IHRoZSBkYXRhIHVzZWQgdG8gZXN0aW1hdGUgdGhlIG1vZGVsIHdlcmUgY2FsY3VsYXRlZCBmcm9tIHRoZSBvcmlnaW5hbCBkYXRhIHNldC7CoA0KDQpHbyB0byB0aGUgb3JpZ2luYWwgcGFwZXIgYW5kIGxvb2sgYXQgRmlndXJlIDEgYW5kIHRoZSBhY2NvbXBhbnlpbmcgdGV4dC7CoCBJZ25vcmUgdCwgdGhlIG51bWJlciBvZiB0cmlwczsgZm9jdXMgb24gdGhlICJwIiBhbmQgIm5vIiBudW1iZXJzLsKgIFZlcmlmeSB0aGF0IHRoZSBudW1iZXIgb2YgIjQgZm9yIDQiIGN1c3RvbWVycyBpbiB0aGUgZmxvdyBjaGFydCBpcyB0aGUgc2FtZSBhcyBpbiBjYWwucmYubWF0cml4LsKgDQoNCioqV2hhdCBhcmUgdGhlIGRpc3RpbmN0IHBhdGhzIChlLmcuLCAwMTAwIG1lYW5zIG5vIGNydWlzZSBpbiB5ZWFyIDEsIGNydWlzZSBpbiB5ZWFyIDIsIG5vIGNydWlzZSBpbiB5ZWFyIDMsIGV0YykgaW4gdGhlIGRpYWdyYW0gdGhhdCBjb21wcmlzZXMgdGhlICh4PTIsIHRfeD00LCBuPTQpIGNlbGwgaW4gY2FsLnJmLk1hdHJpeD8qKg0KDQoqR2l2ZSB0aGVtIGluIHRlcm1zIG9mIDQgYmluYXJ5IGRpZ2l0cyAoMDAwMCBtZWFucyBubyByZXBlYXQgY3J1aXNlcyBpbiBhbnkgb2YgdGhlIGZvdXIgeWVhcnMpKg0KDQpgYGB7cn0NCnRyYW5zIDwtIHRyYW5zJHgNCnR0IDwtIHNlcSgwLCBsZW5ndGgodHJhbnMpLTEsIGJ5PTEpDQpwYXIobWZyb3c9YygxLDEpKQ0KcGFyKG1haT1jKC44LC44LC4yLC4yKSkNCnBsb3QodHQsdHJhbnMsIHR5cGU9ImIiLCB5bGFiPSJUb3RhbCBudW1iZXIgb2YgY3J1aXNlcyIsIHhsYWI9IlllYXIgc2luY2UgZmlyc3QgY3J1aXNlIiwgbWFpbj0iIiwgeGF4dD0nbicsIHlsaW0gPSBjKDAsNzAwMCkpDQpgYGANCg0KIyBRdWVzdGlvbiAyDQoNCioqRXN0aW1hdGUgdGhlIEJHL0JCIHBhcmFtZXRlcnMsIHVzaW5nICgxLDEsMSwxKSBhcyBzdGFydGluZyBwYXJhbWV0ZXJzLioqIMKgDQoNCipQcm92aWRlIHlvdXIgYW5zd2VyIHdpdGggdHdvIGRlY2ltYWxzIHNlcGFyYXRlZCBieSBhIGRvdCwgbm90IGEgY29tbWEgKGUuZy4gMC4xMikuKg0KDQoqKkluaXRpYWwgUGFyYW1ldGVycyoqOg0KDQpgYGB7cn0NCnBhci5zdGFydCA8LSBjKDEsIDEsIDEsIDEpDQpyZi5tYXRyaXggPC0gY2FsLnJmLm1hdHJpeA0KDQpgYGANCg0KKipCR0JCIEVzdGltYXRpb24qKjoNCg0KYGBge3J9DQpwYXJhbXMgPC0gYmdiYi5Fc3RpbWF0ZVBhcmFtZXRlcnMocmYubWF0cml4LCBwYXIuc3RhcnQpDQpyb3VuZChwYXJhbXMsMikgIyBhbHBoYSwgYmV0YSwgZ2FtbWEsIGRlbHRhDQpgYGANCg0KWyoqTG9nLUxpa2VsaWhvb2QqKl17LnVuZGVybGluZX06DQoNCmBgYHtyfQ0KTEwgPC0gYmdiYi5yZi5tYXRyaXguTEwocGFyYW1zLCByZi5tYXRyaXgpDQpMTA0KYGBgDQoNCiMgUXVlc3Rpb24gMw0KDQoqKldoYXQgaGFwcGVucyBpZiB5b3UgcmVzdHJpY3QgdGhlIG1heCBwYXJhbWV0ZXIgdmFsdWUgdG8gYmUgMTAwP8KgIFlvdSBjYW4gZG8gdGhpcyBieSB1c2luZyB0aGUgb3B0aW9uIG1heC5wYXJhbS52YWx1ZSA9IC7CoCBXaGF0IGFyZSB0aGUgcGFyYW1ldGVyIHZhbHVlcz8qKg0KDQoqUHJvdmlkZSB5b3VyIGFuc3dlciB3aXRoIHR3byBkZWNpbWFscyBzZXBhcmF0ZWQgYnkgYSBkb3QsIG5vdCBhIGNvbW1hIChlLmcuIDAuMTIpLioNCg0KYGBge3J9DQpwYXJhbXMgPC0gYmdiYi5Fc3RpbWF0ZVBhcmFtZXRlcnMocmYubWF0cml4LCBwYXIuc3RhcnQsIG1heC5wYXJhbS52YWx1ZSA9IDEwMCkNCnJvdW5kKHBhcmFtcywgMikNCmBgYA0KDQojIFF1ZXN0aW9uIDQNCg0KKipEb2VzIHRoZSBsb2cgbGlrZWxpaG9vZCByb3VuZGVkIHRvIGEgd2hvbGUgbnVtYmVyIGNoYW5nZSB1c2luZyBlc3RpbWF0ZXMgZnJvbSBRMiBhbmQgUTM/KioNCg0KKipMaWtlbGlob29kKio6DQoNCmBgYHtyfQ0KTEwgPC0gYmdiYi5yZi5tYXRyaXguTEwocGFyYW1zLCByZi5tYXRyaXgpDQpMTCAjIGRpZG4ndCBjaGFuZ2UNCmBgYA0KDQojIFF1ZXN0aW9uIDUNCg0KKipHcmFwaCBvdXQgdGhlIGRpc3RyaWJ1dGlvbnMgb2YgdGhlIHRyYW5zYWN0aW9uIHJhdGUgYW5kIGRyb3BvdXQgcmF0ZSBmb3IgYm90aCBzZXRzIG9mIGVzdGltYXRlcyBmcm9tIFEyIGFuZCBRMy4gSW4gYm90aCBjYXNlcywgd2hpY2ggZGlzdHJpYnV0aW9uIHZhcmllcyB0aGUgbGVhc3QgaW4gdGhlIHBvcHVsYXRpb24/KioNCg0KWypUcmFuc2FjdGlvbiBSYXRlLCB3aGlsZSBhbGl2ZSpdey51bmRlcmxpbmV9Og0KDQpgYGB7cn0NCnRlbXAgPC0gYmdiYi5QbG90VHJhbnNhY3Rpb25SYXRlSGV0ZXJvZ2VuZWl0eShwYXJhbXMpDQpgYGANCg0KWypEcm9wIE91dCBSYXRlKl17LnVuZGVybGluZX06DQoNCmBgYHtyfQ0KdGVtcCA8LSBiZ2JiLlBsb3REcm9wb3V0UmF0ZUhldGVyb2dlbmVpdHkocGFyYW1zKQ0KYGBgDQoNClsqKk1lYW4gb2YgUmF0ZXMqKl17LnVuZGVybGluZX06DQoNCmBgYHtyfQ0KcGFyKG1mcm93PWMoMSwyKSkNCnBhcihtYWk9YyguOCwuOCwuNSwuMikpDQp0ZW1wPC1iZ2JiLlBsb3RUcmFuc2FjdGlvblJhdGVIZXRlcm9nZW5laXR5KHBhcmFtcykNCnBhcihtYWk9YyguOCwuOCwuNSwuMikpDQp0ZW1wPC1iZ2JiLlBsb3REcm9wb3V0UmF0ZUhldGVyb2dlbmVpdHkocGFyYW1zKQ0KDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQpjYXQoImF2ZyB0cmFucyByYXRlID0iLHJvdW5kKHBhcmFtc1sxXS8oc3VtKHBhcmFtc1sxOjJdKSksMiksICJcbiIpDQoNCmNhdCgiYXZnIGRyb3BvdXQgcmF0ZSA9Iixyb3VuZChwYXJhbXNbM10vKHN1bShwYXJhbXNbMzo0XSkpLDIpLCAiXG4iKQ0KYGBgDQoNCiMgUXVlc3Rpb24gNg0KDQoqKkluIHRoZSA0XnRoXiB5ZWFyIGFmdGVyIHRoZSBmaXJzdCBwdXJjaGFzZSwgaG93IG1hbnkgYWN0dWFsIHJlcGVhdCBjcnVpc2VzIHdlcmUgdGhlcmUsIGFuZCBob3cgbWFueSBhcmUgcHJlZGljdGVkIGJ5IHRoZSBCR0JCIG1vZGVsICh1c2luZyBRMiBlc3RpbWF0ZXMpPyoqDQoNCipQcm92aWRlIHlvdXIgYW5zd2VyIHdpdGggemVybyBkZWNpbWFscyAoZS5nLiAxMjAgb3IgLTEyMCkuKg0KDQpgYGB7cn0NCiMgdHJhbnNbMjo1XSAtPiAjIG9mIHVzZXJzIHdobyByZXBlYXQgY3J1aXNlcyBiZXR3ZWVuIHBlcmlvZCAxIGFuZCA0DQoNCnByZWQgPC0gYmdiYi5QbG90VHJhY2tpbmdJbmMocGFyYW1zLCByZi5tYXRyaXgsIHRyYW5zWzI6NV0sIHh0aWNrbGFiID0gc2VxKDEsNCkpDQpwcmVkDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQpjYXQoInByZWRpY3RlZCA9Iixyb3VuZChwcmVkWzIsNF0pLCAiXG4iKQ0KY2F0KCJhY3R1YWwgPSIscm91bmQocHJlZFsxLDRdKSwgIlxuIikNCmBgYA0KDQojIFF1ZXN0aW9uIDcNCg0KKipBY2NvcmRpbmcgdG8gdGhlIG1vZGVsLCB3aGF0IGlzIHRoZSBwcmVkaWN0ZWQgbnVtYmVyIG9mIGNydWlzZXMgaW4gdGhlIG5leHQgNCB5ZWFycyBmb3Igc29tZW9uZSB3aG8gdG9vayBhIGNydWlzZSBldmVyeSB5ZWFyIHNvIGZhciAodXNpbmcgUTIgZXN0aW1hdGVzKT8qKg0KDQoqUHJvdmlkZSB5b3VyIGFuc3dlciB3aXRoIHR3byBkZWNpbWFscyBzZXBhcmF0ZWQgYnkgYSBkb3QsIG5vdCBhIGNvbW1hIChlLmcuIDAuMTIpLioNCg0KWyoqSW5kaXZpZHVhbC1MZXZlbCBQcmVkaWN0aW9uKipdey51bmRlcmxpbmV9Og0KDQpgYGB7cn0NCmNvbXAgPC0gYmdiYi5IZWF0bWFwSG9sZG91dEV4cGVjdGVkVHJhbnMocGFyYW1zLCBuLmNhbD00LCBuLnN0YXI9NCkNCmNvbXANCmBgYA0KDQpTb21lb25lIHdobyB0b29rIGEgY3J1aXNlIGV2ZXJ5IHllYXIgKEY9NCkgc28gZmFyIChSPTQsIHBlcmlvZCBvZiBsYXN0IHB1cmNoYXNlKQ0KDQpgYGB7cn0NCnJvdW5kKGNvbXBbNSw1XSwyKQ0KYGBgDQoNCiMgUXVlc3Rpb24gOA0KDQoqKldoYXQgaXMgdGhlIFJMViBmb3Igc29tZW9uZSB3aG8gaGFzIHRha2VuIGEgY3J1aXNlIGV2ZXJ5IHllYXIgc28gZmFyIChGPVI9NCksIGFzc3VtaW5nIGVhY2ggY3J1aXNlIHlpZWxkcyBvbiBhdmVyYWdlIFwkNjAwIGluIHByb2ZpdCwgYW5kIHRoZSBkaXNjb3VudCByYXRlIGlzIDAuMSAodXNpbmcgUTMgZXN0aW1hdGVzKT8qKg0KDQoqUHJvdmlkZSB5b3VyIGFuc3dlciB3aXRoIHplcm8gZGVjaW1hbHMsIHdpdGhvdXQgdGhlIGRvbGxhciBzaWduIChlLmcuIDEyMCBvciAtMTIwWyoqKS4qKl17LnVuZGVybGluZX0qDQoNClsqKkZpcnN0LCB3ZSBuZWVkIENMVioqXXsudW5kZXJsaW5lfToNCg0KYGBge3J9DQptIDwtIDYwMA0KDQpCR0JCQ0xWPC1mdW5jdGlvbihwYXJhbXMsbSxkLFQpIHsNCnBhcmFtczwtdW5uYW1lKHBhcmFtcykNCmFsPC1wYXJhbXNbMV0NCmJlPC1wYXJhbXNbMl0NCmdhPC1wYXJhbXNbM10NCmRlPC1wYXJhbXNbNF0NCkRFVDwtMSAgICMgYXQgdGltZSB6ZXJvIHRoZXJlIGhhcyB0byBiZSBhIHB1cmNoYXNlDQpmb3IgKGkgaW4gMTpUKSB7DQogICAgREVUPC1ERVQrKGFsLyhhbCtiZSkpKihiZXRhKGdhLGRlK2kpL2JldGEoZ2EsZGUpKSoxLygxK2QpXntpfQ0KfQ0KQ0xWPW0qREVUICAjIGNvbnZlcnQgZGlzY291bnQgZXhwZWN0ZWQgcHVyY2hhc2VzIGludG8gZXhwZWN0ZWQgdmFsdWUNCnJldHVybihDTFYpICAgICNyZXR1cm4gdGhlIENMVg0KfQ0KYGBgDQoNCmBgYHtyfQ0KQ0xWIDwtIEJHQkJDTFYocGFyYW1zID0gcGFyYW1zLCBtPTYwMCxkPS4xLFQ9MjAwKQ0KQ0xWDQpgYGANCg0KWyoqTm93IHdlIGNhbiBnZXQgUkxWKipdey51bmRlcmxpbmV9Og0KDQpgYGB7cn0NCm0gPC0gNjAwDQpERVJUIDwtIGJnYmIucmYubWF0cml4LkRFUlQocGFyYW1zLCByZi5tYXRyaXggPSBjYWwucmYubWF0cml4LCBkPTAuMSkNClJMViA8LSBtKkRFUlQNCg0KUkxWbWF0cml4IDwtIGNiaW5kKGNhbC5yZi5tYXRyaXgscm91bmQoUkxWKSkgDQpSTFZtYXRyaXgNCmBgYA0KDQpgYGB7ciwgZWNobz1GQUxTRX0NCmNhdCgiUTYgUkxWIGZvciA0IGZvciA0ID0gJCIsIFJMVm1hdHJpeFsxLCJyb3VuZChSTFYpIl0sICJcbiIpDQpgYGANCg==