Assignment 2: RFM Analysis

Case 1

Ben’s Knick Knacks sells a consumer durable product with a unit margin of $161.50 and per customer mailing costs of $0.3343. They have formed 126 segments based on past purchase history. They do a test mailing to 3.24% of their database. You can see the outcomes of the test in file knick_knack_test.csv. The columns are segment number, the number of people in that segment that were mailed, and the number of people who responded.

ktest <- read_csv("knick_knack_test.csv")

Setting the parameters:

m <- 161.50
c <- 0.3343
nseg <- 126
tsize <- 0.0324

1. What is the response breakeven threshold for mailing?

Provide your answer with four decimals separated by a dot, not a comma (e.g. 0.1234).

brk = c/m

## Breakeven Point: 0.0021

2. How many segments would you target (out of 126)?

Provide a number (e.g. 34).

ktest <- ktest %>% 
  mutate(resp_rate = x_s/m_s) %>% 
  arrange(desc(resp_rate))
ktest <- as.data.frame(ktest)

bp <- barplot(ktest[,7])
axis(1, at = bp[,1], labels=ktest[,1], cex.axis=0.7, las=2)
abline(h=brk)
text(85, brk, "breakeven", cex=1, pos=3, col="black")

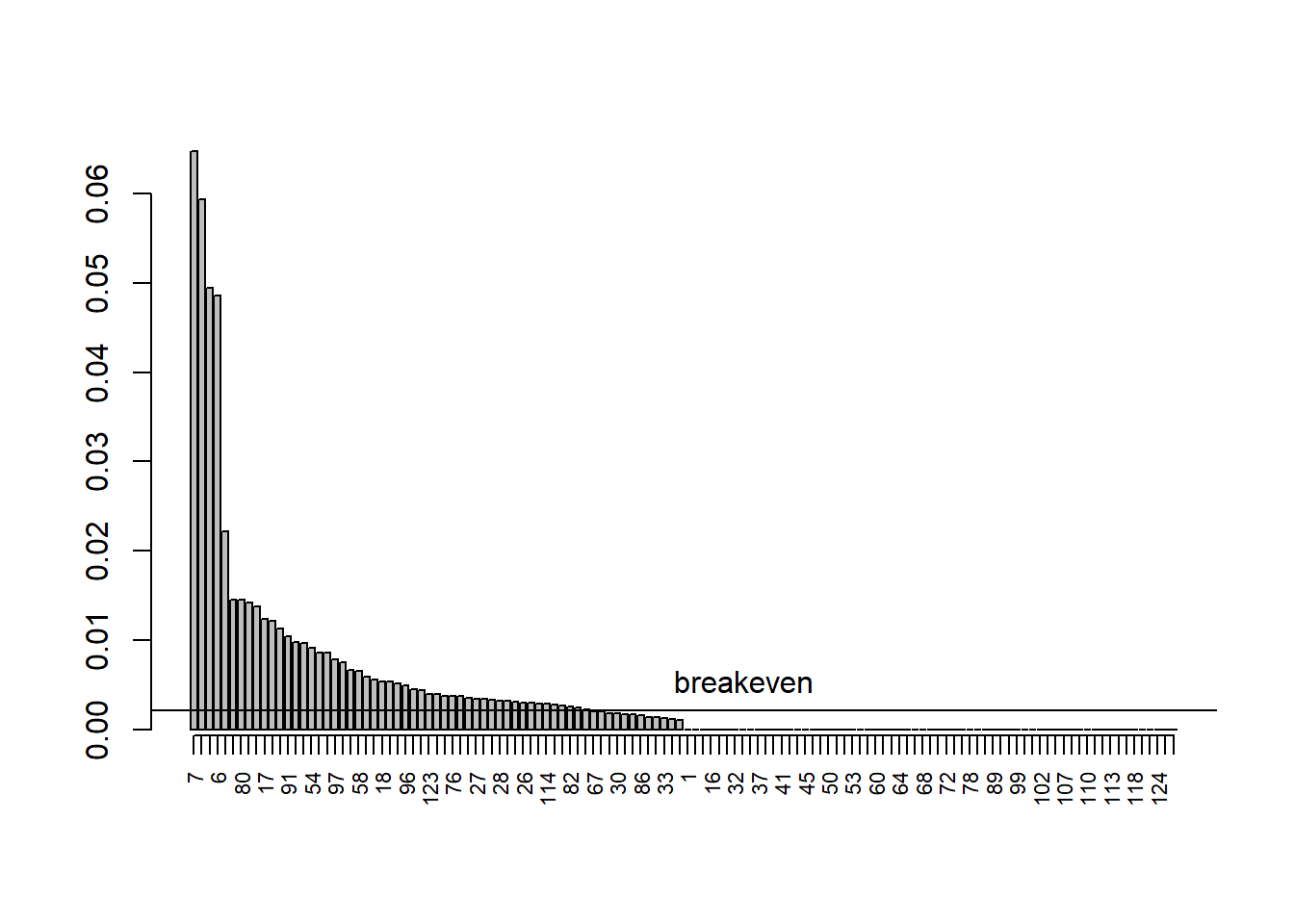
How many segments should be targeted? What segments are they? As a percentage of the total segments?

n_segments <- sum(ktest$resp_rate >= brk)

## Optimal Number of segments: 51

Case 2

The company ended up rolling out to 71 segments. See the file knick_knack_roll.csv for the segments, whether they were rolled out to, the number of customers rolled out to in each segment, and the responses.

kroll <- read_csv("knick_knack_roll.csv")

You can now compare the test response rate and the rollout response rates (for the 71 segments that were rolled out to).

kroll <- kroll %>% 
  mutate(resp_rate = case_when(Resp_s== 0 ~ 0 , 
                               TRUE ~ Resp_s/Roll_s)) %>% 
  arrange(desc(resp_rate))
kroll1 <- kroll[!is.na(kroll$Resp_s), ] # 71 segments

How well do test rates predict roll rates? One way to measure this is the correlation. If they predict perfectly, this would be 1.

3. Calculate the correlation between test and roll rates.

Provide your answer with three decimals separated by a dot, not a comma (hint; in the cor function use, use = “complete.obs”).

ktest_arrange0 <- ktest %>% arrange(Segment)
kroll_arrange0 <- kroll %>% arrange(Segment)

corr1 <- cor(ktest_arrange0$resp_rate, kroll_arrange0$resp_rate, use = "complete.obs")

round(corr1, 3)

## [1] 0.915

4. Fit a beta-binomial model to the test data: What is the parameter estimate for the first shape parameter a?

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

ktest <- ktest %>% 
  mutate(nonx_s = m_s-x_s)
ktest_arrange0 <- ktest %>% 
  mutate(nonx_s = m_s-x_s)

We run the MLE Estimator:

fit <- vglm(cbind(ktest_arrange0$x_s, ktest_arrange0$nonx_s) ~ 1, betabinomialff, trace=TRUE)

## VGLM    linear loop  1 :  loglikelihood = -201.76139
## VGLM    linear loop  2 :  loglikelihood = -200.56819
## VGLM    linear loop  3 :  loglikelihood = -200.54941
## VGLM    linear loop  4 :  loglikelihood = -200.54812
## VGLM    linear loop  5 :  loglikelihood = -200.54804
## VGLM    linear loop  6 :  loglikelihood = -200.54804
## VGLM    linear loop  7 :  loglikelihood = -200.54804

a <- Coef(fit)[[1]]
b <- Coef(fit)[[2]] 

round(a, 3)

## [1] 0.439

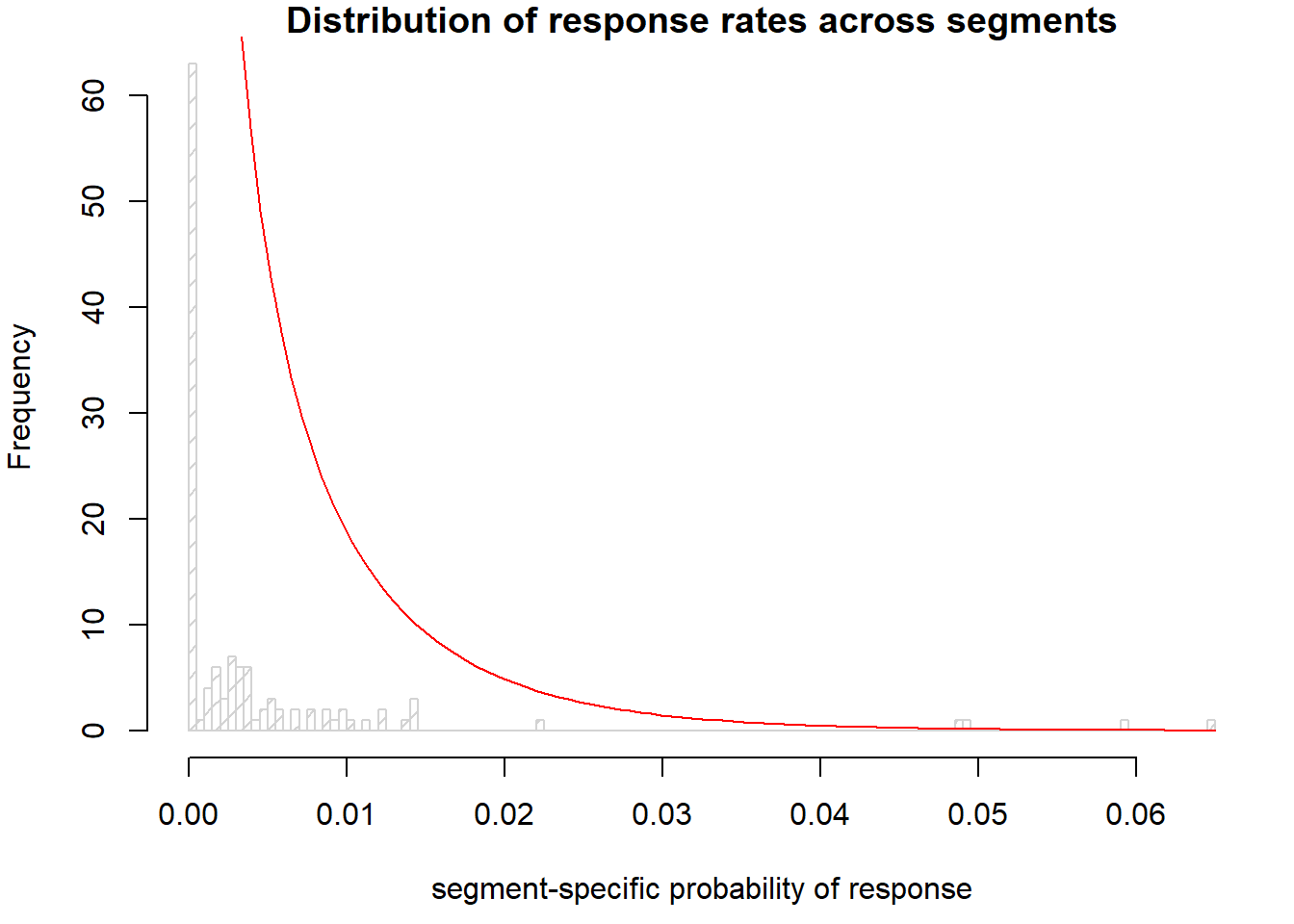
5. What is the shape of the beta distribution you estimate?

x <- seq(0,.05,length=1000)

par(mai=c(.9,.8,.2,.2))
hist(ktest$resp_rate, density=10, breaks=100, main="Distribution of response rates across segments", xlab="segment-specific probability of response")
curve(dbeta(x, a, b), add = TRUE,  type="l", col="red")

6. How many segments would you target using the Beta-Binomial model?

ktest1 <- ktest %>% 
  mutate(post_mean_resp = (a+x_s)/(a+b+m_s))

## [1] 66

Comparison Plot:

plot(ktest1$resp_rate, xaxt="n",col="red",xlab="RFM segments",ylab="response rate (x/n) and posterior mean response rate")
points(ktest1$post_mean_resp, col='blue')
legend('topleft',legend=c("estimate response rate", "posterior expected response rate"),col=c("red","blue"), pch=1)
axis(1, at = 1:126, labels=ktest1$Segment, cex.axis=0.7, las=2)
abline(h=brk)
text(120, brk, "breakeven", cex=1, pos=3, col="black")

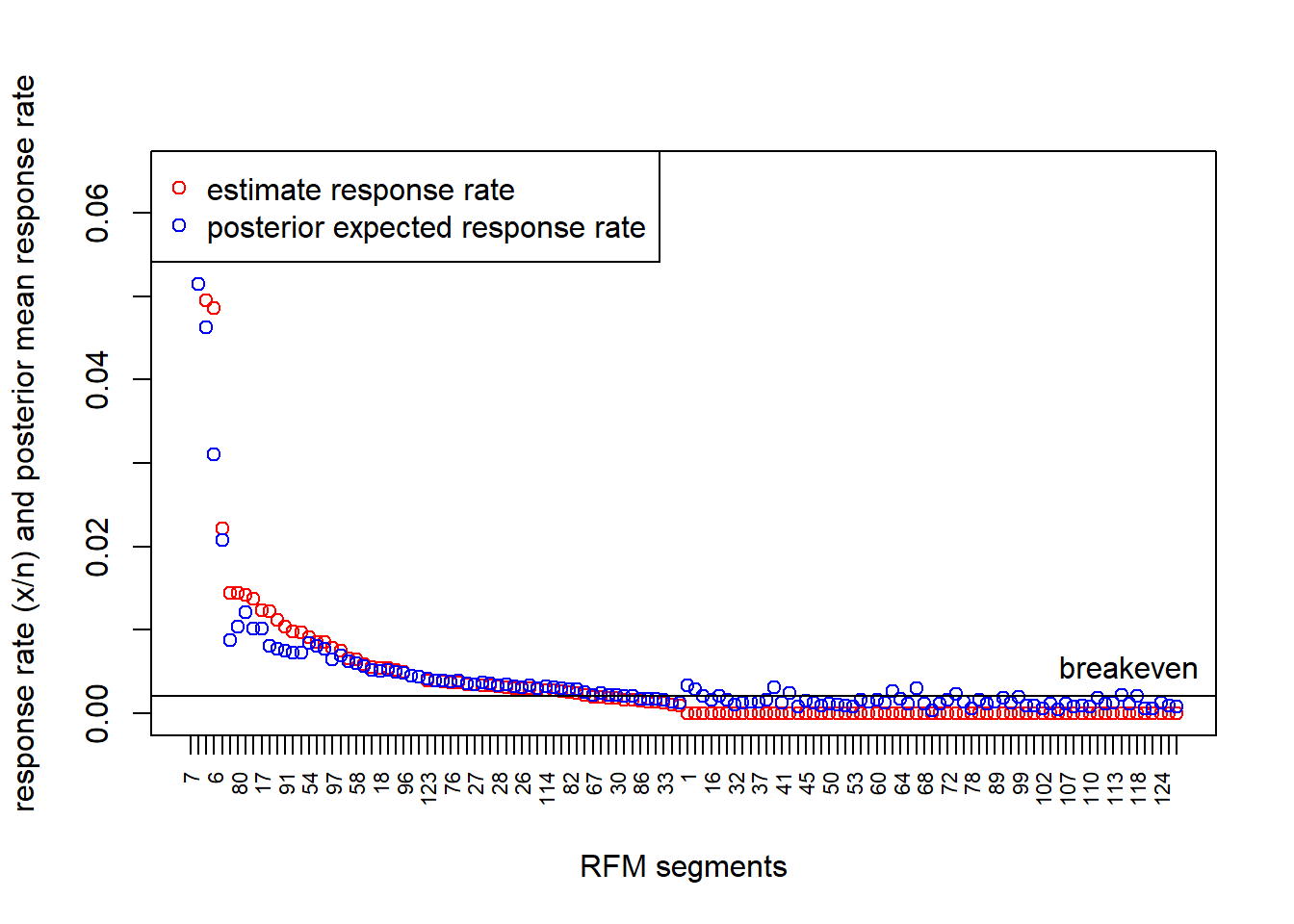
7. Does the posterior mean response rate fit the rollout response rate better than the test response rate?

Calculate the correlation as in Question 3.

#need to arrange!

ktest_arrange <- ktest1 %>% arrange(Segment)
kroll_arrange <- kroll %>% arrange(Segment)

corr1 <- cor(ktest_arrange$resp_rate, kroll_arrange$resp_rate, use = "complete.obs")
round(corr1, 3) #0.915

## [1] 0.915

corr2 <- cor(ktest_arrange$post_mean_resp, kroll_arrange$resp_rate, use = "complete.obs")
round(corr2, 3) #0.916

## [1] 0.916

8. Calculate the Return on Investment (ROI) of targeting using the posterior mean.

For the 71 segments we observe rollout outcomes for, calculate the return on investment of targeting using the posterior mean. Use the data on the actual number of customers mailed and responses, along with margin and cost per marketing, in your calculation.

Provide your answer with zero decimals without the percent sign (e.g. 120).

We Calculate ROI for 71 segments

# what about the return on investment ROI?

sum_profit = sum(kroll2$RFMprofit*kroll2$Roll_s)
sum_cost = sum(kroll2$RFMcost*kroll2$Roll_s)
roi <- sum_profit/sum_cost 

## ROI: 401 %