Quiz 7: CLV - Non-contractual settings

In this assignment, we will use a different data set with 10000 customers and 13 periods total. We estimate the model on the first 7 (calibration) and test it on the final 6 periods (holdout).  

cal.rf.matrix <- read.csv("cal.rf.matrix.csv")
trans <- read.csv("annual_transactions.csv")
holdout <- read.csv("holdout.trans.rf.matrix.csv")

Question 1

Create a graph of aggregate transactions per year. What are the total number of purchases in year 8 after the first purchase?

Provide your answer without any decimals (e.g. 12)

trans <- trans$x

par(mfrow=c(1,1))
par(mai=c(.8,.8,.2,.2))
plot(seq(1,13,1),trans, type="b", ylab="Total number of repeat transactions", xlab="Year since first purchase", main="", xaxt='n')
axis(1, at = seq(0, 13, by = 1))
abline(v=7.5,col = "red", lwd = 2)
text(x = 6,y = 4500,"Calibration", cex=1, pos=3, col="black", font = 2)
text(x = 9,y = 4500,"Validation", cex=1, pos=3, col="black", font = 2)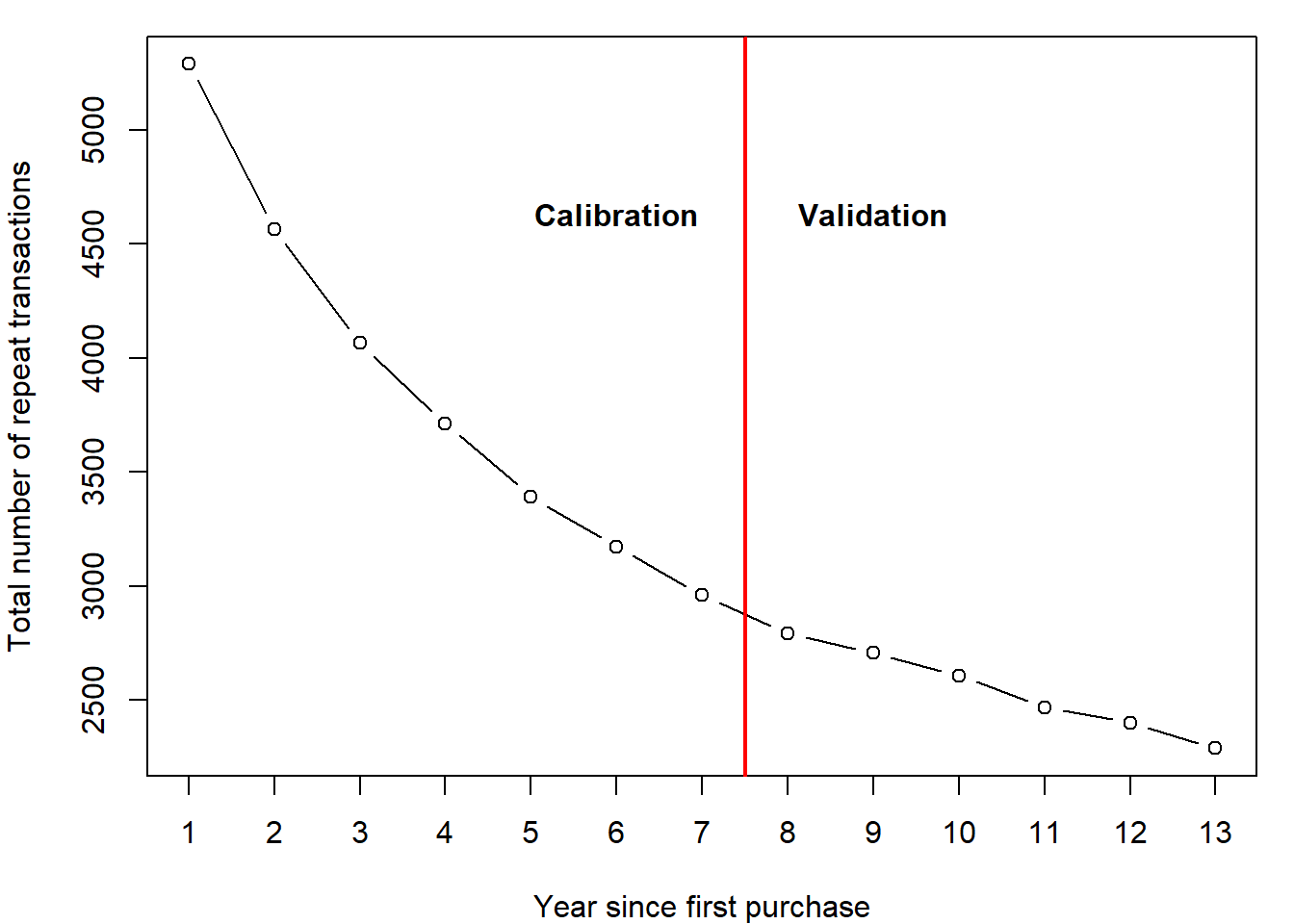

Question 2

Estimate the BG/BB parameters using the calibration data, the first seven years. What are the parameters?

Provide your answers with a dot and two decimals (e.g. 0.12)

Initial Parameters:

rf.matrix <- cal.rf.matrix
par.start <- c(1, 1, 1, 1)

MLE Estimation:

params <- bgbb.EstimateParameters(rf.matrix, par.start)
round(params, 2)

## [1] 1.32 0.67 0.51 2.09

## Check log-likelihood of the params:
LL <- bgbb.rf.matrix.LL(params, rf.matrix)
LL

## [1] -33013

Question 3

Graph out the distributions of the transaction rate and dropout rate. What are the average values of each in the population?

Provide your answer with a dot and two decimals (e.g. 0.12)

Average transaction rate:

round(params[1]/(params[1]+params[2]),2)

## [1] 0.66

bgbb.PlotTransactionRateHeterogeneity(params)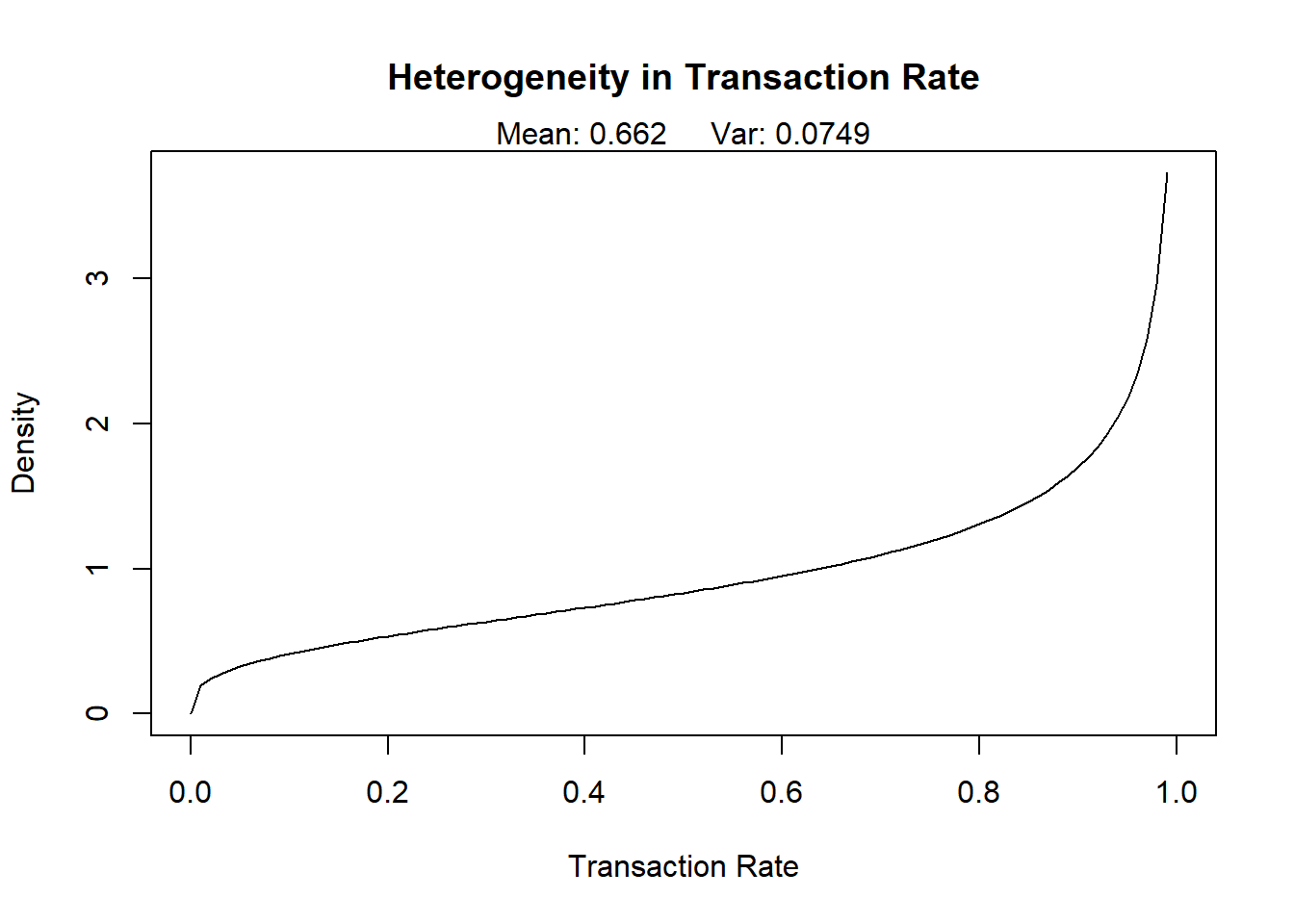

##   [1] 0.000 0.193 0.241 0.275 0.303 0.326 0.346 0.365 0.382 0.398 0.413 0.427 0.441 0.454 0.466 0.479 0.490 0.502 0.513 0.524 0.535 0.545 0.556 0.566 0.576 0.586 0.596 0.606 0.616 0.625 0.635 0.645 0.654 0.664 0.674 0.683 0.693 0.703 0.712 0.722 0.732 0.742 0.751 0.761 0.771 0.781 0.792 0.802 0.812
##  [50] 0.823 0.834 0.844 0.855 0.867 0.878 0.889 0.901 0.913 0.925 0.938 0.950 0.963 0.976 0.990 1.004 1.018 1.033 1.048 1.064 1.080 1.096 1.114 1.131 1.150 1.169 1.190 1.211 1.233 1.256 1.280 1.306 1.334 1.363 1.394 1.427 1.463 1.502 1.545 1.592 1.644 1.702 1.768 1.844 1.933 2.040 2.173 2.345 2.586
##  [99] 2.963 3.730   Inf

Average dropout rate:

round(params[3]/(params[3]+params[4]),2)

## [1] 0.2

bgbb.PlotDropoutRateHeterogeneity(params)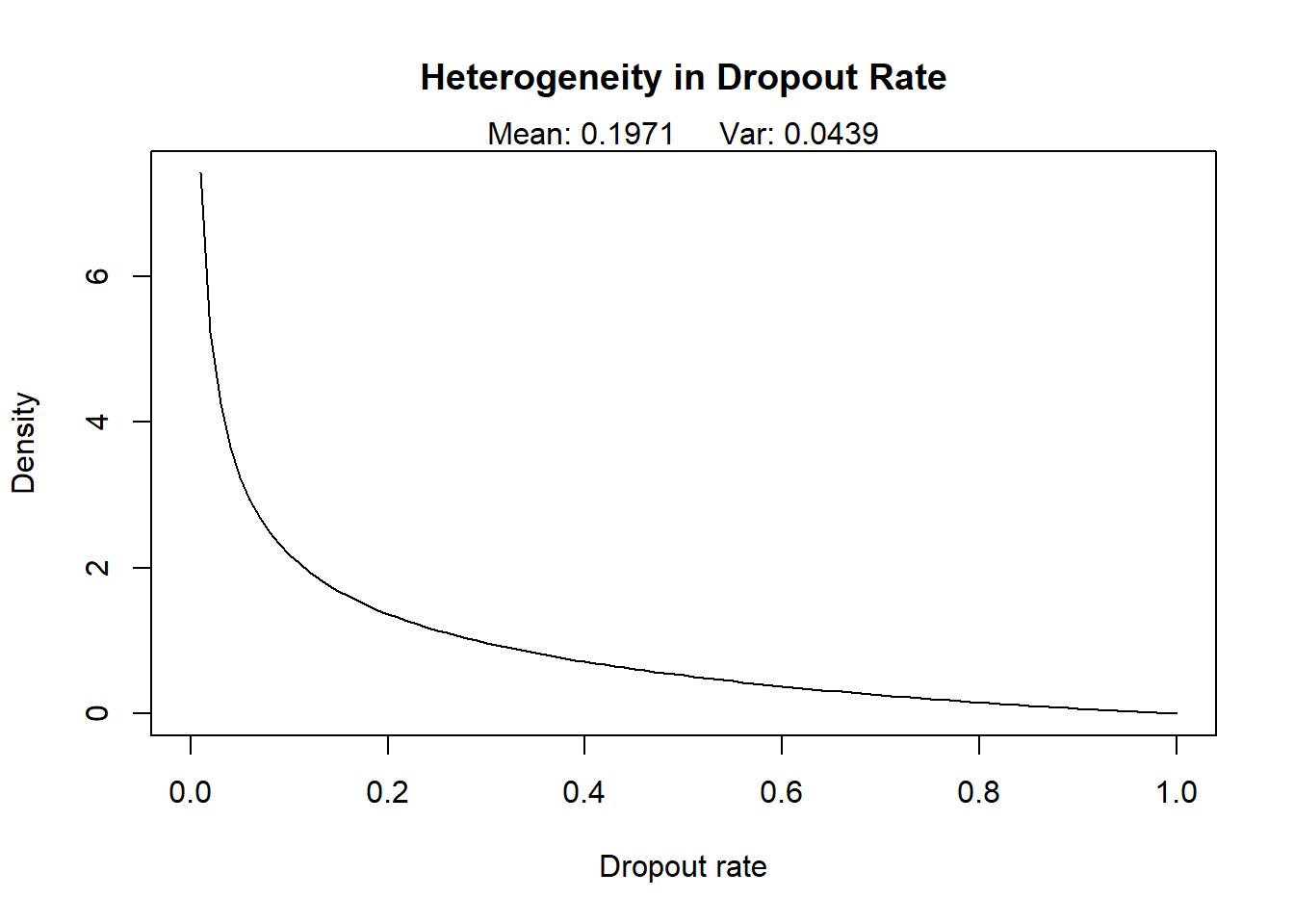

##   [1]     Inf 7.41359 5.23277 4.24797 3.65150 3.23854 2.92955 2.68628 2.48774 2.32130 2.17884 2.05487 1.94553 1.84800 1.76019 1.68047 1.60761 1.54060 1.47864 1.42107 1.36737 1.31707 1.26980 1.22525 1.18312 1.14320 1.10527 1.06915 1.03469 1.00176 0.97022 0.93998 0.91093 0.88299 0.85608 0.83014
##  [37] 0.80509 0.78088 0.75746 0.73478 0.71280 0.69148 0.67078 0.65067 0.63112 0.61209 0.59356 0.57552 0.55792 0.54076 0.52402 0.50767 0.49170 0.47609 0.46083 0.44590 0.43129 0.41699 0.40299 0.38927 0.37583 0.36265 0.34973 0.33706 0.32463 0.31243 0.30045 0.28870 0.27715 0.26581 0.25467 0.24373
##  [73] 0.23298 0.22241 0.21202 0.20181 0.19177 0.18190 0.17220 0.16266 0.15328 0.14405 0.13499 0.12607 0.11731 0.10870 0.10024 0.09193 0.08377 0.07576 0.06790 0.06019 0.05265 0.04527 0.03805 0.03102 0.02419 0.01758 0.01124 0.00524 0.00000

Question 4

Graph out the actual and predicted transactions per year. What is the expected level of transactions in year 8 after the first purchase?

Provide your answer with zero decimals (e.g. 12)

Aggregate Forecasting:

pred <- bgbb.PlotTrackingInc(params, rf.matrix, trans)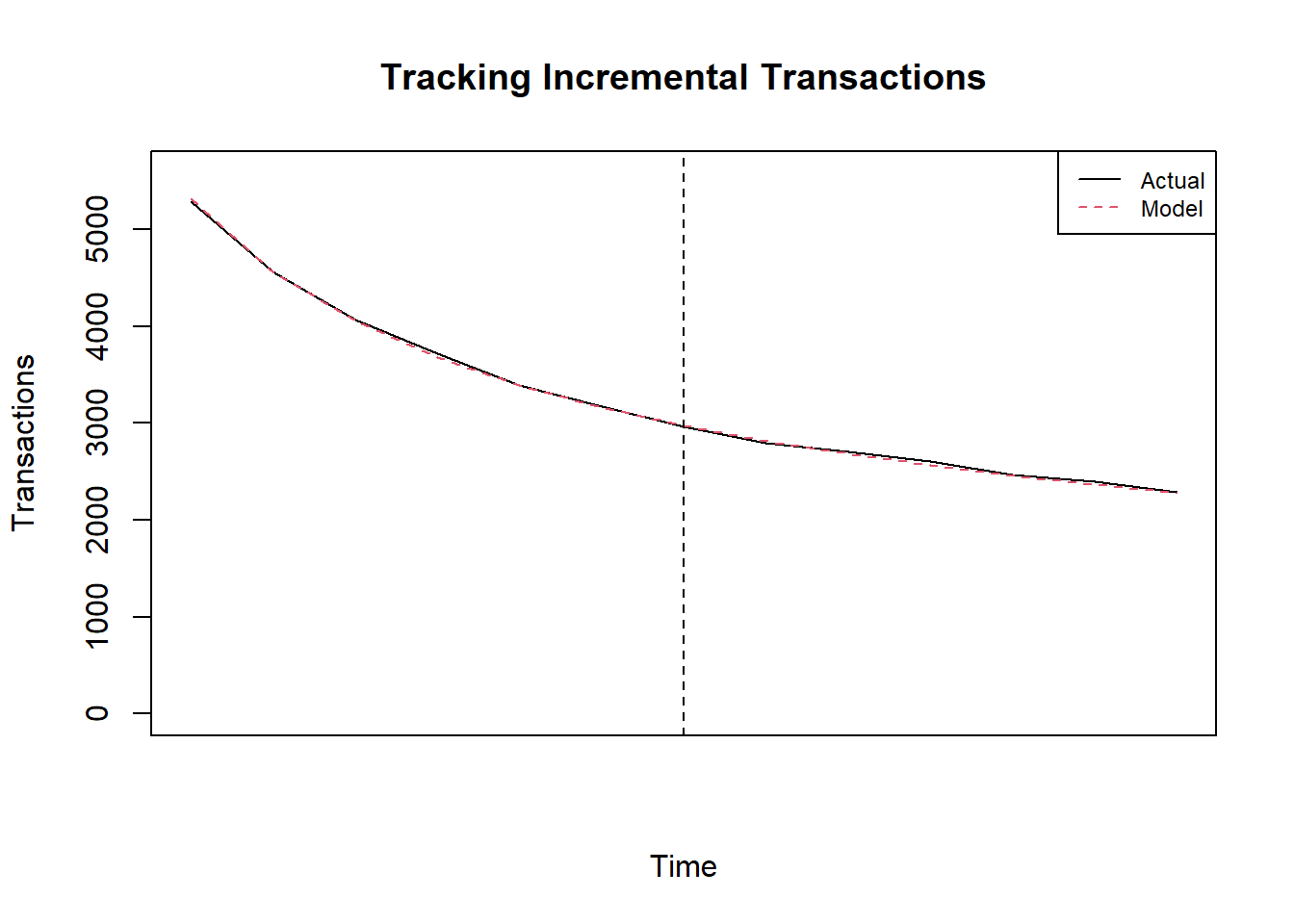

## Q4 = 2817

Question 5

According to the model, what is the predicted number of transactions in the holdout for a customer who was “7 for 7” in the calibration period?  What is the actual number of holdout transactions for these customers?

Provide your answer with a dot and two decimals (e.g. 0.12)

Predicted:

bgbb.HeatmapHoldoutExpectedTrans(params, n.cal = 7, n.star = 6)

## layout: widths =  0.05 4 , heights =  0.25 4 ; lmat=
##      [,1] [,2]
## [1,]    0    3
## [2,]    2    1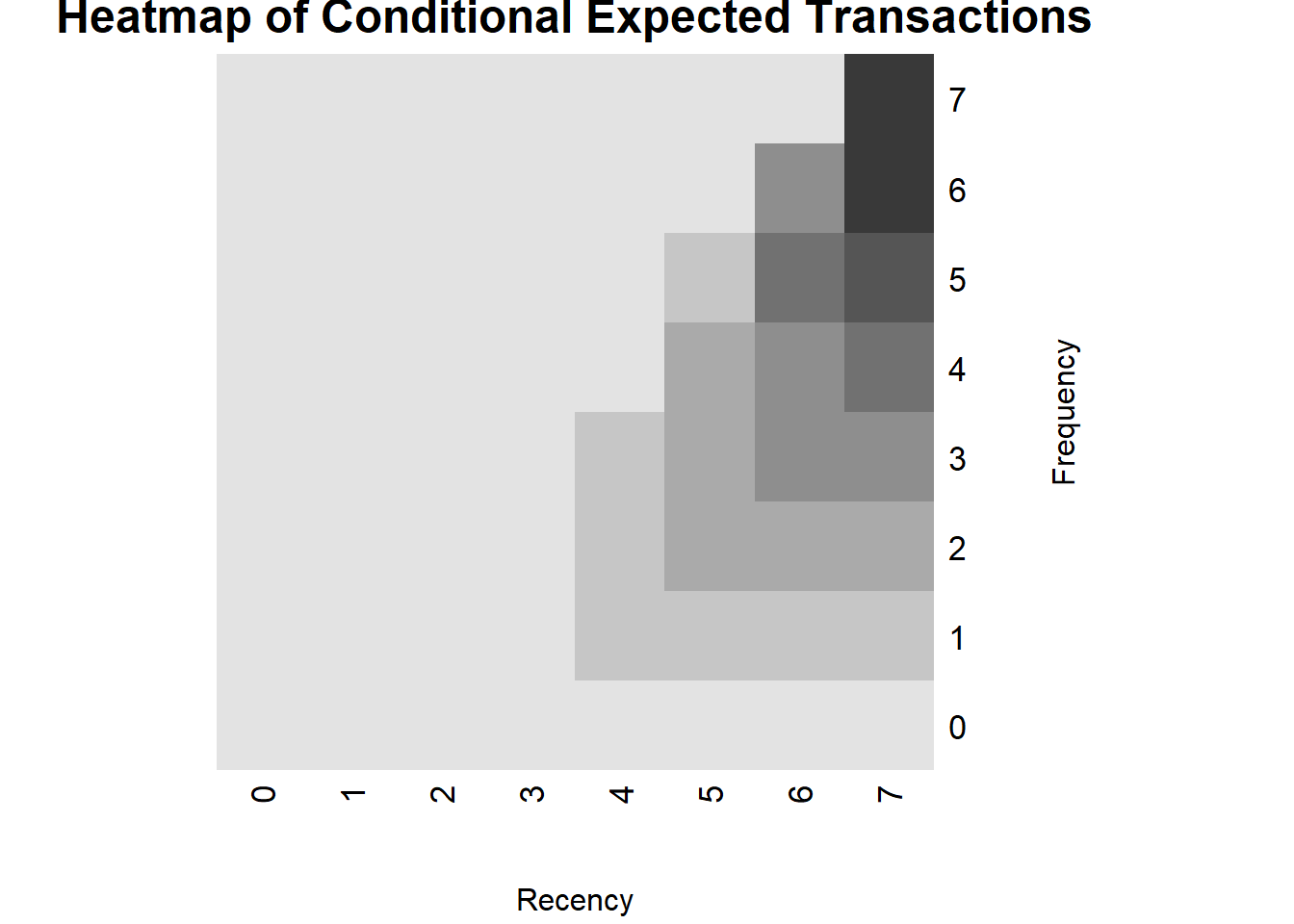

##        0      1      2     3     4     5    6    7
## 0 0.0575 0.0000 0.0000 0.000 0.000 0.000 0.00 0.00
## 1 0.0000 0.0589 0.2629 0.551 0.830 1.049 1.21 1.31
## 2 0.0000 0.0000 0.0701 0.394 0.913 1.383 1.70 1.88
## 3 0.0000 0.0000 0.0000 0.109 0.692 1.553 2.15 2.45
## 4 0.0000 0.0000 0.0000 0.000 0.235 1.401 2.53 3.01
## 5 0.0000 0.0000 0.0000 0.000 0.000 0.698 2.75 3.58
## 6 0.0000 0.0000 0.0000 0.000 0.000 0.000 2.36 4.15
## 7 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.00 4.71

Actual:

cbind(cal.rf.matrix, holdout)

##    x t.x n.cal custs    x
## 1  0   0     7  2900  152
## 2  1   1     7   933   50
## 3  1   2     7   218   58
## 4  2   2     7   489   29
## 5  1   3     7    95   67
## 6  2   3     7   160   61
## 7  3   3     7   292   14
## 8  1   4     7    73   75
## 9  2   4     7   113  104
## 10 3   4     7   130   74
## 11 4   4     7   189   50
## 12 1   5     7    51   59
## 13 2   5     7    98  113
## 14 3   5     7   131  219
## 15 4   5     7   137  250
## 16 5   5     7   161  153
## 17 1   6     7    34   39
## 18 2   6     7    92  155
## 19 3   6     7   168  367
## 20 4   6     7   162  426
## 21 5   6     7   204  569
## 22 6   6     7   209  479
## 23 1   7     7    50   56
## 24 2   7     7   104  190
## 25 3   7     7   205  493
## 26 4   7     7   320  956
## 27 5   7     7   401 1492
## 28 6   7     7   666 2783
## 29 7   7     7  1215 5738

# take total transactions for last row divided by customers:

act <- holdout$x[29]/cal.rf.matrix[29,4] #ind=29 has 7 of 7, the last obs.

## Actual = 4.72

Question 6

What is the CLV, assuming each transaction yields on average 50 in profit and the discount rate is 0.1? You can use 200 periods for the sum.

Provide your answer with zero decimals (e.g. 12)

BGBBCLV<-function(params,m,d,T) {
params<-unname(params)
al<-params[1]
be<-params[2]
ga<-params[3]
de<-params[4]
DET<-1   # at time zero there has to be a purchase
for (i in 1:T) {
    DET<-DET+(al/(al+be))*(beta(ga,de+i)/beta(ga,de))*1/(1+d)^{i}
}
CLV=m*DET  # convert discount expected purchases into expected value
return(CLV)    #return the CLV
}

CLV:

CLV <- BGBBCLV(params = params, m=50,d=.1,T=200)
CLV

## [1] 203

Question 7

What is the RLV for a 7 for 7 customer? Again, assume each transaction yields on average 50 in profit, and the discount rate is 0.1.  

Provide your answer with zero decimals (e.g. 12)

m <- 50
DERT <- bgbb.rf.matrix.DERT(params, rf.matrix = cal.rf.matrix, d=0.1)
RLV <- m*DERT

RLVmatrix <- cbind(cal.rf.matrix,round(RLV)) 
RLVmatrix

##    x t.x n.cal custs round(RLV)
## 1  0   0     7  2900          4
## 2  1   1     7   933          4
## 3  1   2     7   218         18
## 4  2   2     7   489          5
## 5  1   3     7    95         39
## 6  2   3     7   160         28
## 7  3   3     7   292          8
## 8  1   4     7    73         58
## 9  2   4     7   113         64
## 10 3   4     7   130         49
## 11 4   4     7   189         16
## 12 1   5     7    51         74
## 13 2   5     7    98         97
## 14 3   5     7   131        109
## 15 4   5     7   137         98
## 16 5   5     7   161         49
## 17 1   6     7    34         85
## 18 2   6     7    92        119
## 19 3   6     7   168        151
## 20 4   6     7   162        178
## 21 5   6     7   204        193
## 22 6   6     7   209        166
## 23 1   7     7    50         92
## 24 2   7     7   104        132
## 25 3   7     7   205        172
## 26 4   7     7   320        212
## 27 5   7     7   401        251
## 28 6   7     7   666        291
## 29 7   7     7  1215        331

RLV:

max(RLV)

## [1] 331

Question 8

Consider a charity with just one opportunity for people to donate per year. Consider a donor has donated 3 times in the past five years with the last donation occurring in year 4. In the context of the BG/BB model, what are the donor’s sufficient statistics: n, t_x, and x

n=5
t_x = 4
x = 3

Assume that = 0.6 and Θ = 0.2.

What is the likelihood of this customer’s donations?

Provide your answer with a dot and three decimals (e.g. 0.123)

n <- 5
t_x <- 4
x <- 3

p <- 0.6
theta <- 0.2

\[ L(p,\theta|x, t_x,n)=p^x(1-p)^{n-x}(1-\theta)^n +\sum^{n-t_x-1}_{j=0}p^x(1-p)^{t_x-x+j}\theta(1-\theta)^{t_x+j} \]

a <- (p^3)*(1-p)*((1-theta)^4)*theta
b <- (p^3)*(1-p)^2*((1-theta)^5) ## the last obs. does not have theta

likelihood <- a+b
round(likelihood,3)

## [1] 0.018

Question 9

What is the probability that the customer is alive at the end?

Provide your answer with a dot and three decimals (e.g. 0.123)

\[ \Pr(\text{alive at }n|x,t_x,n)=\frac{p^x(1-p)^{n-x}(1-\theta)^n}{L(p,\theta|x,t_x,n)} \]

(p^3)*((1-p)^2)*((1-theta)^5)/likelihood

## [1] 0.615