Quiz 4: Subset Selection, LASSO & Trees

Question 1

Let’s use a decision tree to predict churn. Use the data set telco_test.csv. Make sure all the string variables are loaded as factors by using the following statement:

telco <- read.csv('telco_test.csv', stringsAsFactors = TRUE)

# Churn as dummy
Churn.num <- as.numeric(as.factor(telco$Churn))-1
rbar <- mean(Churn.num)

Fit a tree that stops growing when the child branch has below 50 observations or when the deviance improves by less than 0.001.

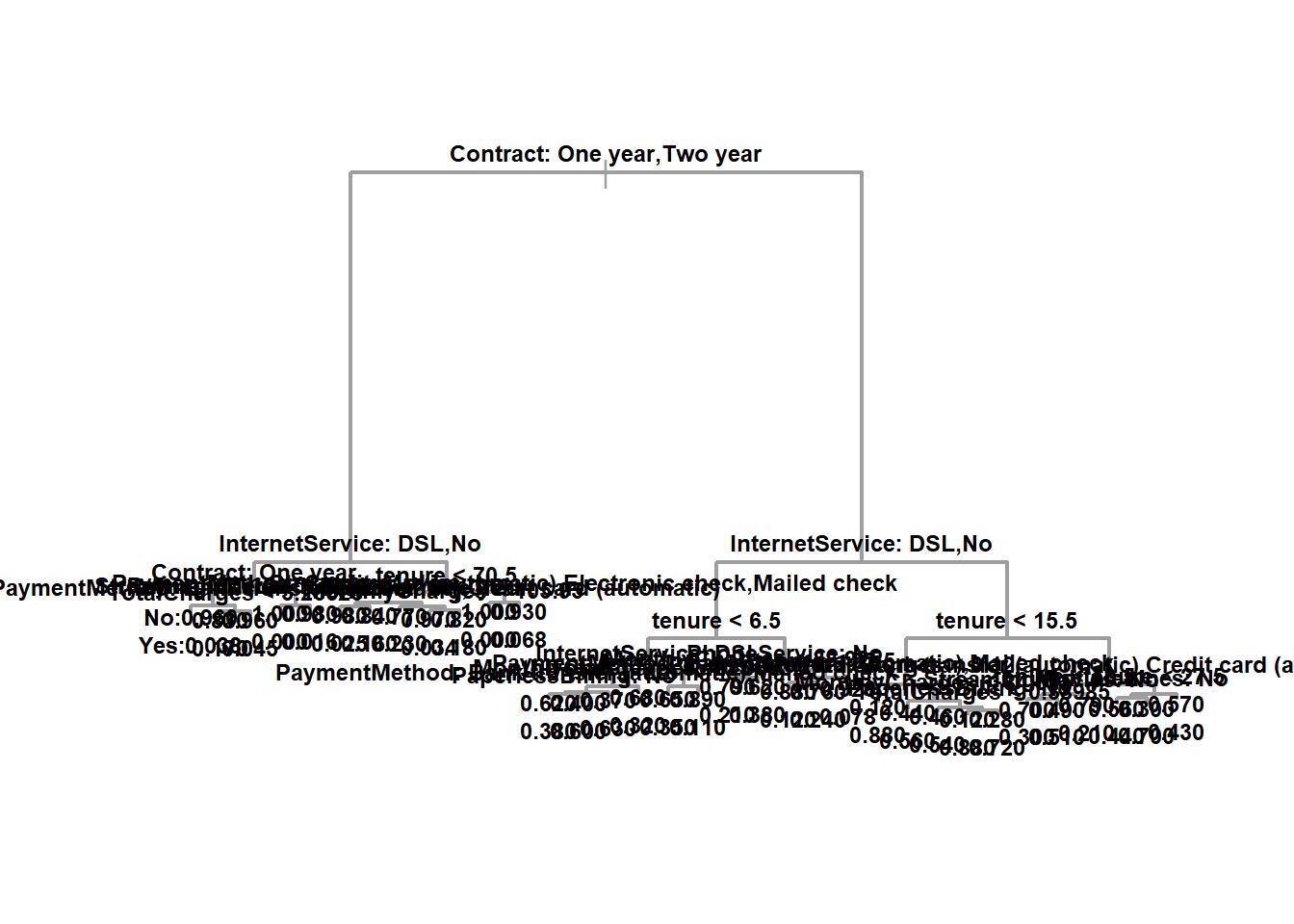
What variables are used in this tree? Check all that apply.

tree <- tree(as.factor(Churn) ~., data = telco, mindev=0.001, mincut=50)
summary(tree)

## 
## Classification tree:
## tree(formula = as.factor(Churn) ~ ., data = telco, mindev = 0.001, 
##     mincut = 50)
## Variables actually used in tree construction:
##  [1] "Contract"         "InternetService"  "StreamingMovies"  "TotalCharges"     "PaymentMethod"    "tenure"           "MonthlyCharges"   "PaperlessBilling" "PhoneService"     "MultipleLines"   
## Number of terminal nodes:  34 
## Residual mean deviance:  0.798 = 3920 / 4920 
## Misclassification error rate: 0.191 = 946 / 4949

par(mfrow=c(1,1))
plot(tree, col=8, lwd=2)
text(tree, label = "yprob", cex=.75, font=2, digits = 2, pretty=0)

Question 2

According to this model, what is the probability that a female senior citizen, with no partners, no dependents, who has been a customer for 12 months, with phone service, without multiple lines, with DSL, no online security, no online backup, no device protection, with tech support and streaming TV, without streaming movies, on a one year contract, no paperless billing, pays by mailed check, with monthly charges of 30 and total charges of 1000, churns?

Provide your answer with a dot and two decimals (e.g. 0.12)

newdata1 <- data.frame(gender = as.factor(2), SeniorCitizen=1, 
                       Partner=as.factor(1), Dependents=as.factor(1), 
                       tenure=12,PhoneService=as.factor(2),
                       MultipleLines=as.factor(1), InternetService=as.factor(2), 
                       OnlineSecurity=as.factor(1), OnlineBackup=as.factor(1),
                       DeviceProtection=as.factor(1), TechSupport=as.factor(2), 
                       StreamingTV=as.factor(2), StreamingMovies=as.factor(1), 
                       Contract=as.factor(levels(telco$Contract))[2], 
                       PaperlessBilling=as.factor(1), PaymentMethod=as.factor(1), 
                       MonthlyCharges=30, TotalCharges=10)

Now we can predict:

pred_tree <- predict(tree, newdata = newdata1, type="vector")
round(pred_tree[2],2)

## [1] 0.04

Question 3

What’s the percent of correctly predicted churners, the true positive rate, using a threshold of 0.5 to classify predictions?

Provide your answer without a percent sign and with zero decimals (e.g. 12)

We predict again, but now using all the data:

pred_tree <- predict(tree, newdata = telco, type="vector")

prob_resp <- pred_tree[,2]
sum(prob_resp>0.5) # but there is no above 0.5

## [1] 1109

confusion_matrix <- (table(telco$Churn, prob_resp > 0.5))
confusion_matrix <- as.data.frame.matrix(confusion_matrix)

colnames(confusion_matrix) <- c("No", "Yes")

confusion_matrix$Percentage_Correct <- confusion_matrix[1,]$No/(confusion_matrix[1,]$No+confusion_matrix[1,]$Yes)*100
confusion_matrix[2,]$Percentage_Correct <- confusion_matrix[2,]$Yes/(confusion_matrix[2,]$No+confusion_matrix[2,]$Yes)*100

print(confusion_matrix)

##       No Yes Percentage_Correct
## No  3272 378               89.6
## Yes  568 731               56.3

## Hit Rate: 56.3

Question 4

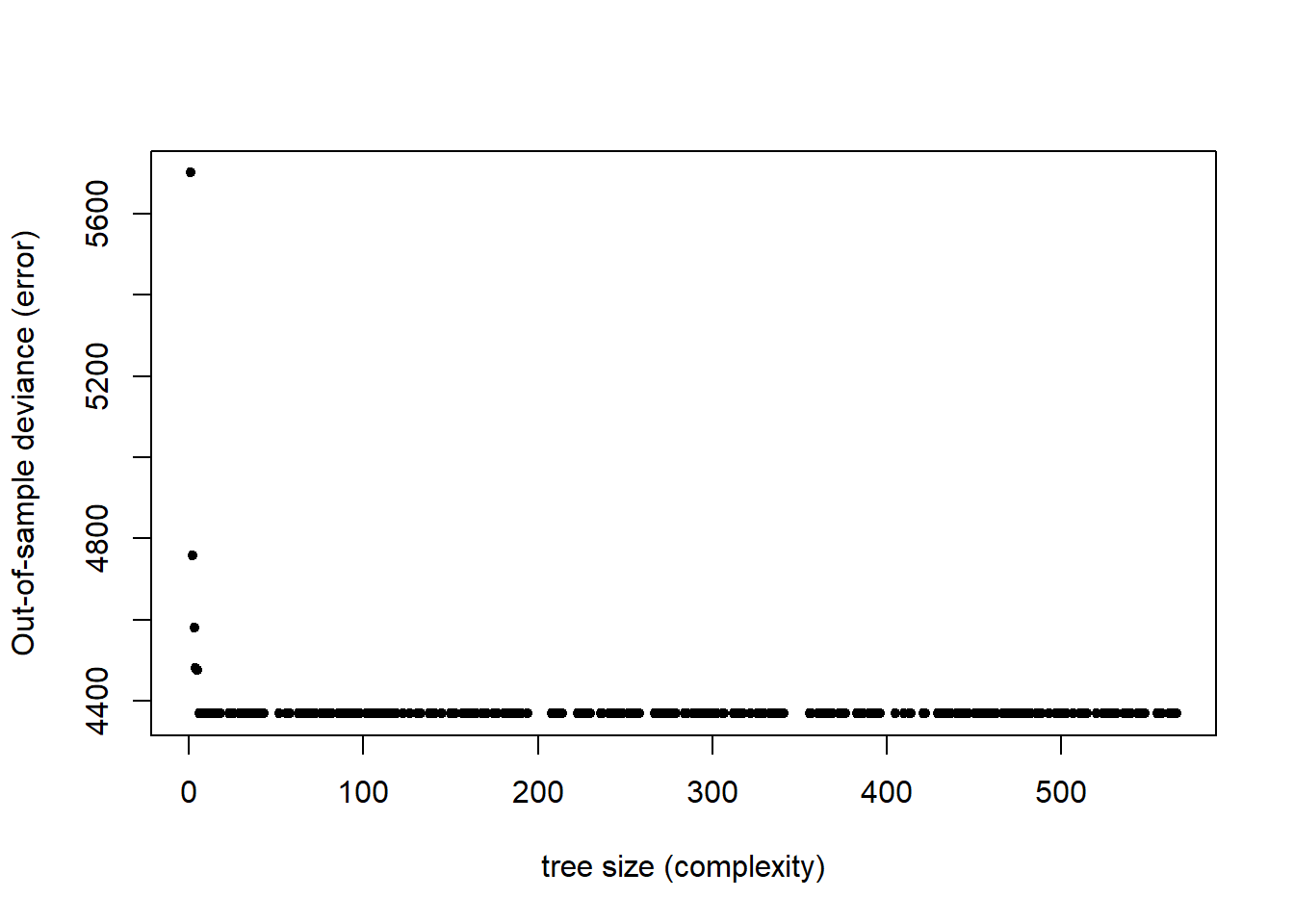
We’re now going to use 10-fold cross-validation to prune the tree. Start with the most complex tree by setting mindev and mincut to 0. Use 10 fold cross-validation to find the smallest tree that has the lowest deviance rounded to the first whole number.  

How many leaves (terminal nodes) are in this tree?

We start with the complex tree:

tree_complex <- tree(as.factor(Churn) ~., data = telco, mindev=0, mincut=0)

we now can do the cross-validation K=10:

cv.tree.complex <- cv.tree(tree_complex, K=10)

How many leaves?

par(mfrow=c(1,1))
plot(cv.tree.complex$size, cv.tree.complex$dev, xlab="tree size (complexity)", ylab="Out-of-sample deviance (error)", pch=20)

Question 5

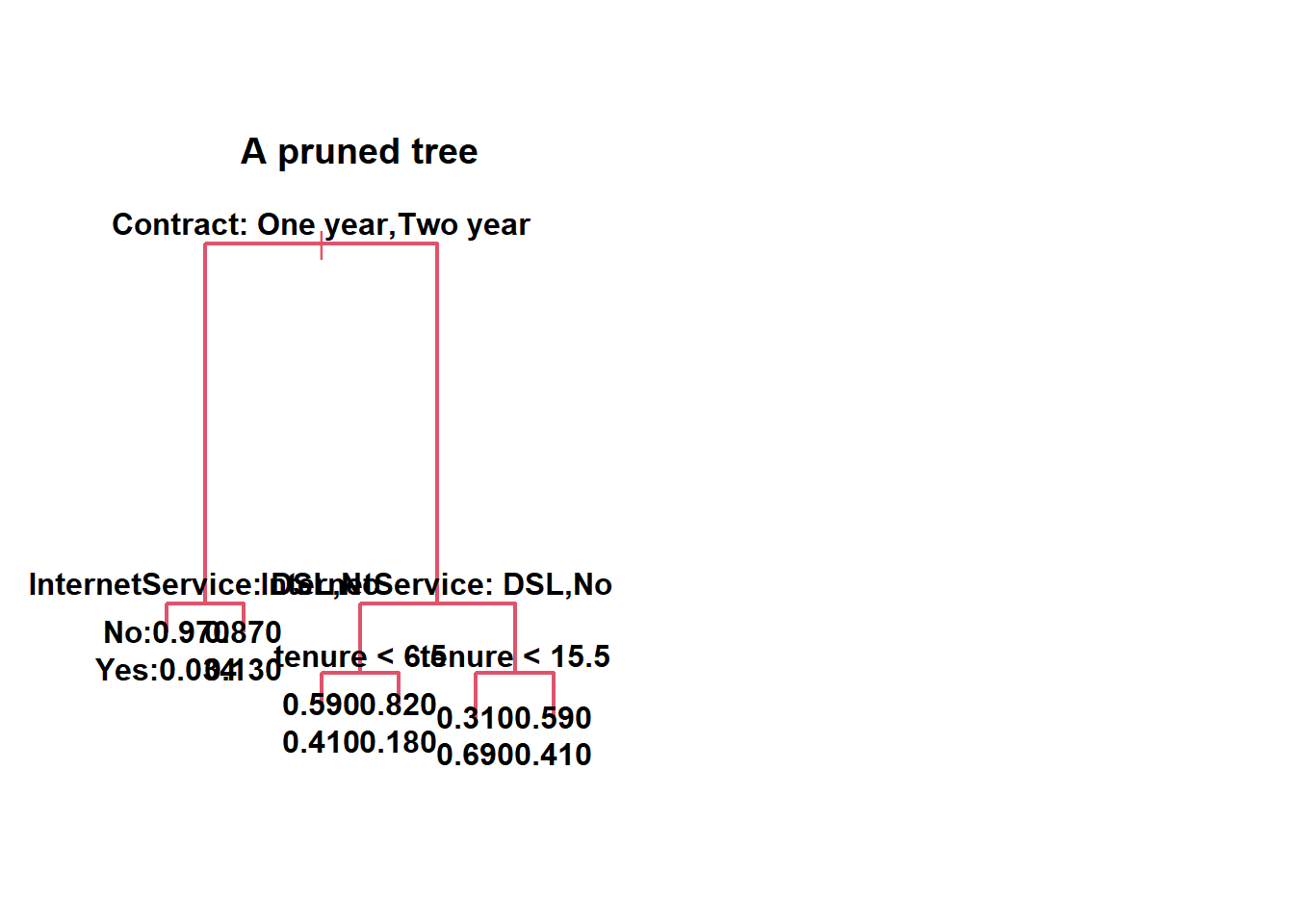
According to this pruned model, what’s the probability of someone with a one-year contract, who has been a customer for 12 months, and has no internet service, churns?

Provide your answer with a dot and three decimals (e.g. 0.123)

We choose our best model with 6 leaves:

tree_cut <- prune.tree(tree_complex, best=6)
summary(tree_cut)

## 
## Classification tree:
## snip.tree(tree = tree_complex, nodes = c(13L, 15L, 5L, 4L, 12L, 
## 14L))
## Variables actually used in tree construction:
## [1] "Contract"        "InternetService" "tenure"         
## Number of terminal nodes:  6 
## Residual mean deviance:  0.872 = 4310 / 4940 
## Misclassification error rate: 0.209 = 1034 / 4949

We can predict now:

par(mfrow=c(1,2), oma = c(0, 0, 2, 0))
plot(tree_cut, col=10, lwd=2)
text(tree_cut, cex=1, label="yprob", font=2, digits = 2, pretty = 0)
title(main="A pruned tree")

Question 6

Fit a random forest to the data, with 1000 trees, minimum node size of 25, using average probabilities rather than classifications (probability = TRUE).  

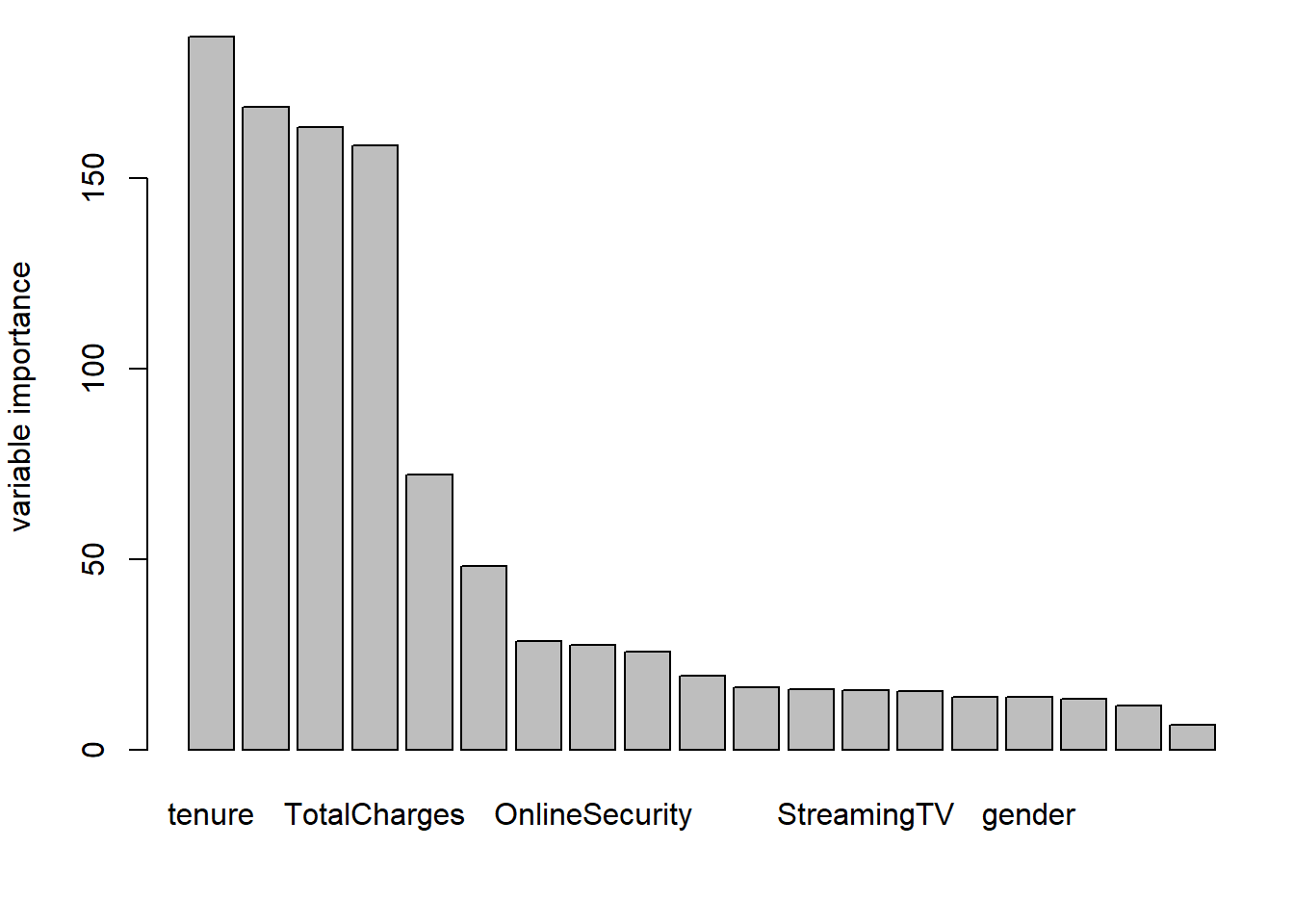
What is the most important variable according to this? Give the variable name.

telco_rf <- ranger(Churn ~ ., data = telco, 
                   write.forest=TRUE, 
                   num.trees = 1000, 
                   min.node.size = 25, 
                   importance = "impurity", 
                   probability=TRUE, 
                   seed = 19103)

Variable Importance:

sort(telco_rf$variable.importance, decreasing = TRUE)

##           tenure   MonthlyCharges         Contract     TotalCharges  InternetService    PaymentMethod      TechSupport   OnlineSecurity PaperlessBilling    SeniorCitizen    MultipleLines     OnlineBackup      StreamingTV       Dependents  StreamingMovies           gender          Partner 
##           187.23           168.65           163.55           158.63            72.32            48.20            28.58            27.63            25.72            19.50            16.37            15.92            15.68            15.52            14.03            13.89            13.39 
## DeviceProtection     PhoneService 
##            11.63             6.67

par(mfrow=c(1,1))
par(mai=c(.9,.8,.2,.2))
barplot(sort(telco_rf$variable.importance, decreasing = TRUE), ylab = "variable importance")

Question 7

Apply the most complex tree that you started with in question 4; also apply the pruned tree and the random forest to the holdout data set.

telco.holdout <- read.csv('telco_holdout.csv', stringsAsFactors = TRUE)

# Churn as dummy
Churn.num <- as.numeric(as.factor(telco.holdout$Churn))-1

What is the area under the curve for the tree?

Provide your answer with a dot and two decimals (e.g. 0.12)

Let’s apply every model at once to the holdout:

#take only "Yes"
pred_cut <- predict(tree_cut, newdata=telco.holdout, type="vector")[,2]

pred_complex <- predict(tree_complex, newdata=telco.holdout, type="vector")[,2]

pred_rf <- predict(telco_rf, data=telco.holdout)$predictions[,2]

# Observed churn as number
churn.num <- as.numeric(telco.holdout$Churn)-1

Area Under the Curve:

roc(churn.num, pred_cut)

## 
## Call:
## roc.default(response = churn.num, predictor = pred_cut)
## 
## Data: pred_cut in 1513 controls (churn.num 0) < 570 cases (churn.num 1).
## Area under the curve: 0.809

par(mfrow=c(1,3))
par(mai=c(.9,.8,.2,.2))
plot(roc(as.numeric(telco.holdout$Churn)-1, pred_cut), print.auc=TRUE, ylim=c(0,1),
     col="black", lwd=1, main="ROC curve", xlab="Specificity: true negative rate", ylab="Sensitivity: true positive rate", xlim=c(1,0))

## Setting levels: control = 0, case = 1

## Setting direction: controls < cases

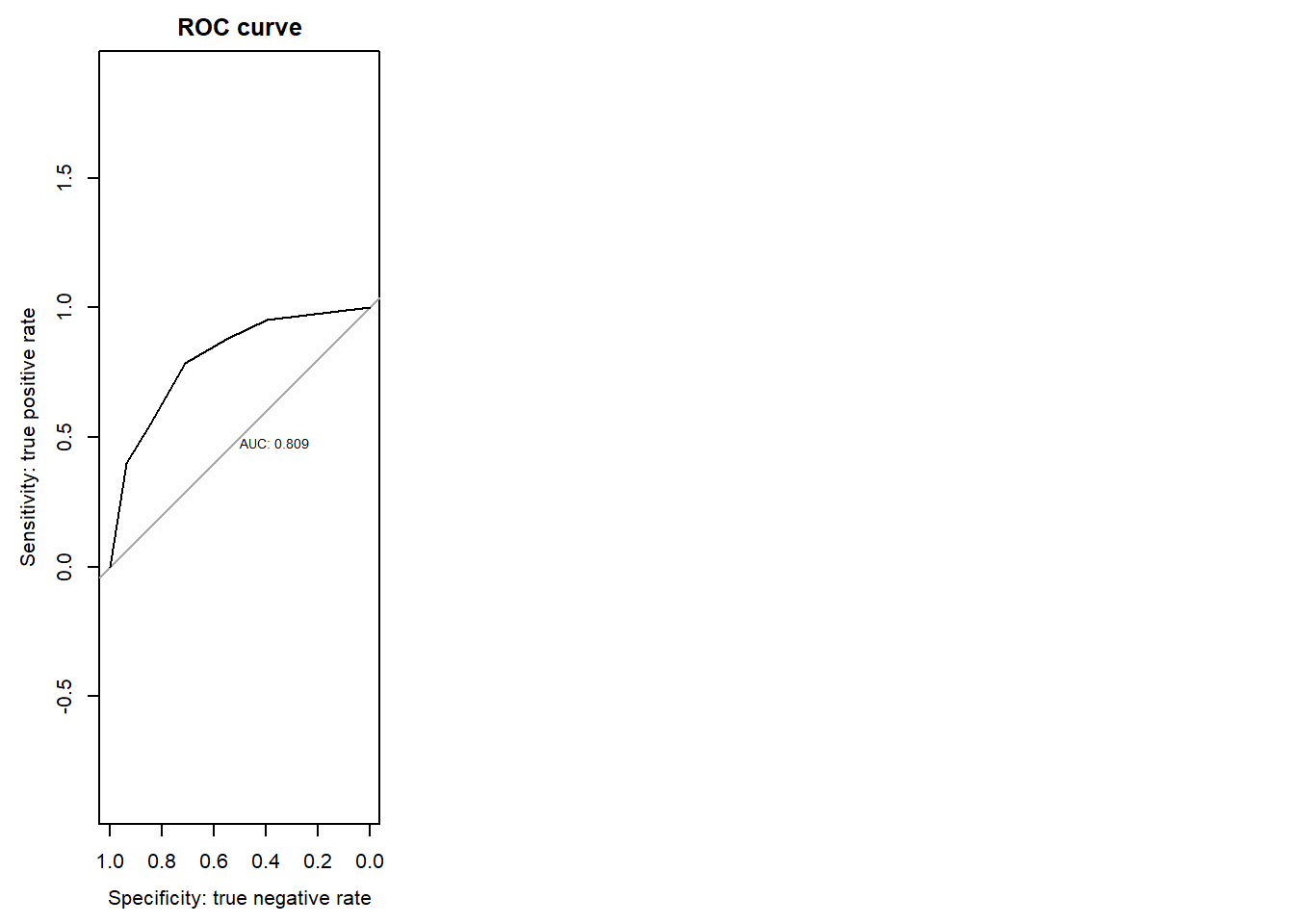
Question 8

What is the area under the curve for the random forest?

Provide your answer with a dot and two decimals (e.g. 0.12)

roc(churn.num, pred_rf)

## 
## Call:
## roc.default(response = churn.num, predictor = pred_rf)
## 
## Data: pred_rf in 1513 controls (churn.num 0) < 570 cases (churn.num 1).
## Area under the curve: 0.84

Question 9

What is the area under the curve for the complex tree?

Provide your answer with a dot and two decimals (e.g. 0.12)

round(roc(churn.num, pred_complex)$auc,2)

## [1] 0.7

Question 10

Using the random forest in the holdout data, if you were targeting the top 3 deciles, what percentage of total churners would you target?

Provide your answer without a percent sign and with zero decimals (e.g. 12)

We start creating the deciles:

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}

# Deciles
telco.holdout$prob <-pred_rf
prob_decile <- ntiles(telco.holdout$prob, 10)

# Churn as numeric:
telco.holdout$Churn.num <- as.numeric(as.factor(telco.holdout$Churn))-1

# Dataset:
tbl <- data.frame(cbind(telco.holdout$prob, prob_decile, telco.holdout$Churn.num))
colnames(tbl)<-c("predicted","decile", "actual")

Create lift table by decile

# First: average churn rate by decile
lift <- aggregate(actual~decile, data = tbl, mean)
colnames(lift)[2]<-"actual churn rate"

# lift is the actual churn rate in the decile divided by average overall churn rate
lift[,3]<-lift[,2]/mean(telco.holdout$Churn.num)
colnames(lift)[3]<-"lift"

# order for highest to lowest
lift<-lift[order(-lift$decile),]

lift[,4]<-cumsum(lift$actual)/sum(lift$actual)*100
colnames(lift)[4]<-"cumulative lift"

lift %>% 
  kbl() %>%
  kable_styling()

	decile	actual churn rate	lift	cumulative lift
10	10	0.761	2.780	27.8
9	9	0.606	2.214	50.0
8	8	0.418	1.529	65.3
7	7	0.359	1.311	78.4
6	6	0.226	0.826	86.7
5	5	0.149	0.545	92.1
4	4	0.105	0.385	96.0
3	3	0.072	0.264	98.6
2	2	0.019	0.070	99.3
1	1	0.019	0.070	100.0