• Question 1
  • Question 2
  • Question 3
  • Question 4
  • Question 5
  • Question 6
  • Question 7
  • Question 8

A telecommunications company (like KPN) wants to implement a proactive churn policy, using logistic regression to predict churn. They assemble a data set of past customers who either churned or stayed, along with several variables that can be used to predict this decision. This data set is called telco_test.csv.

test <- read_csv("telco_test.csv")

Make sure all non-metric variables like gender, senior citizen, partner are coded as a factor (as done in the lab session) except for 3 variables — tenure, monthly charges, and total charges. Use this code:

test$gender <- as.factor(test$gender)
test$PaymentMethod <- as.factor(test$PaymentMethod)

# Change Churn from "no" "yes" to 0 1
test <- test %>%
mutate(Churn = ifelse(Churn == "No",0,1))

Question 1

Let’s focus on the relationship between churn and payment method using just the data.

What is the proportion of churners of people who pay using a mailed check?

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

mailed <- test %>% 
  group_by(PaymentMethod) %>% 
  summarise(n=n(), Churn = sum(Churn), p_churn = round(Churn/n,3))
## The proportion of churners of people who pay using a mailed check is 0.186

Question 2

What is the upper bound of the 95% confidence interval for the proportion of churners of people who pay using a mailed check?

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

churn_pmethod <- test %>% 
  group_by(PaymentMethod) %>% 
  summarise(p_churn = mean(Churn), 
            n_churners = sum(Churn), 
            n=n(),
            p_churn_se = sqrt((p_churn)*(1-p_churn)/n)) %>%
  mutate(lower_CI_pchurn = p_churn - 1.96*p_churn_se, 
         upper_CI_pchurn = p_churn + 1.96*p_churn_se) 

churn_pmethod$upper_CI_pchurn[4] ## 0.209
## [1] 0.2086

Predict churn using gender, senior citizen, tenure (as a continuous variable), payment method, and the interaction between tenure and payment method. Call this model 1.

# fit 
model_1 <- glm(Churn ~ gender + SeniorCitizen + tenure*PaymentMethod, data=test, family = binomial(link="logit"))

Question 3

What is the R2 of model 1?

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.123).

D <- model_1$deviance # get deviance D for each
D0 <- model_1$null.deviance # D_0 is the same for all models
  
R2 <- 1-D/D0
round(R2,3)
## [1] 0.188

Question 4

According to model 1, a customer who pays by mailed check increases or decreases his or her likelihood of churn with each unit increase in tenure.

Report the odds for this customer

Provide your answer with zero decimals without the percent sign (e.g. 120 or -120).

coef1 <- round( (exp(coef(model_1)["tenure"] + coef(model_1)["tenure:PaymentMethodMailed check"])-1 )*100, 0)
## Odds Decreases -6 %

The odds of a customer who pays by mailed check and increase tenure by an unit vs “has a tenure of 1” are different.

Question 5

What is the K-fold cross validation estimate of R2?

Use K = 5, set the seed to 19103. Report the average of the values.

Provide your answer with two decimals separated by a dot, not a comma (e.g. 0.12).

set.seed(19103)
n = nrow(test)
K = 5 # # folds
foldid = rep(1:K, each=ceiling(n/K))[sample(1:n)]
OOS <- data.frame(model1=rep(NA,K))


## pred must be probabilities (0<pred<1) for binomial
  deviance <- function(y, pred, family=c("gaussian","binomial")){
    family <- match.arg(family)
    if(family=="gaussian"){
      return( sum( (y-pred)^2 ) )
    }else{
      if(is.factor(y)) y <- as.numeric(y)>1
      return( -2*sum( y*log(pred) + (1-y)*log(1-pred) ) )
    }
  }

## get null deviance too, and return R2
  R2 <- function(y, pred, family=c("gaussian","binomial")){
  fam <- match.arg(family)
  if(fam=="binomial"){
    if(is.factor(y)){ y <- as.numeric(y)>1 }
  }
  dev <- deviance(y, pred, family=fam)
  dev0 <- deviance(y, mean(y), family=fam)
  return(1-dev/dev0)
  }  

# this part will take several minutes, fitting 3 models K times each
  
for(k in 1:K){
  train = which(foldid!=k) # data used to train
  
  # fit regressions
  model_1 <- glm(Churn ~ gender + SeniorCitizen + tenure*PaymentMethod, data=test[train,], family = binomial(link="logit"))
  
  # predict on holdout data (-train)
  pred1 <- predict(model_1, newdata=test[-train,], type = "response") ##TRAIN DATA not, the WHOLE SAMPLE
  
  # calculate R2
  OOS$model1[k] <- R2(y = test$Churn[-train],pred=pred1, family="binomial")
  
  # print progress
  cat(k, "  ")
    
}
## 1   2   3   4   5
## Average of R2 is 0.18
par(mai=c(.9,.8,.2,.2))  
boxplot(OOS[,1], data=OOS, main=expression(paste("Out-of-Sample R"^"2")),
        xlab="Model", ylab=expression(paste("R"^"2")))

Apply model 1 to the holdout data set, telco_holdout.csv.

holdout_telco <- read_csv("telco_holdout.csv")

## Dummes:
holdout_telco$gender<-as.factor(holdout_telco$gender)
holdout_telco$PaymentMethod<-as.factor(holdout_telco$PaymentMethod)

# Change Churn from "no" "yes" to 0 1
holdout_telco <- holdout_telco %>%
  mutate(Churn = ifelse(Churn == "No",0,1))

Predicting Churning:

# predicted x'beta part of 
xb <- predict(model_1, type = "link", newdata=holdout_telco)
# the predicted probability 
prob <- predict(model_1, type = "response", newdata=holdout_telco)

head(cbind(xb,prob)) %>% 
  kbl() %>%
  kable_styling()
xb prob
-2.9511 0.0497
-1.2190 0.2281
-1.4337 0.1925
-2.1621 0.1032
-4.2539 0.0140
-0.3521 0.4129

Plot:

# first we arrange:
ind <- order(prob)

## PLOT
par(mai=c(.9,.8,.2,.2))
plot(xb[ind],holdout_telco$Churn[ind], pch=4,cex=0.3,col="blue", xlab="x'beta",ylab="P(Churn) on holdout data")
lines(x=xb[ind], y=prob[ind], col="red", lwd=2)
legend('left',legend=c("actual", "predicted (model 1)"),col=c("blue","red"), pch=c(1,NA),lty=c(NA,1), lwd=c(NA,2))

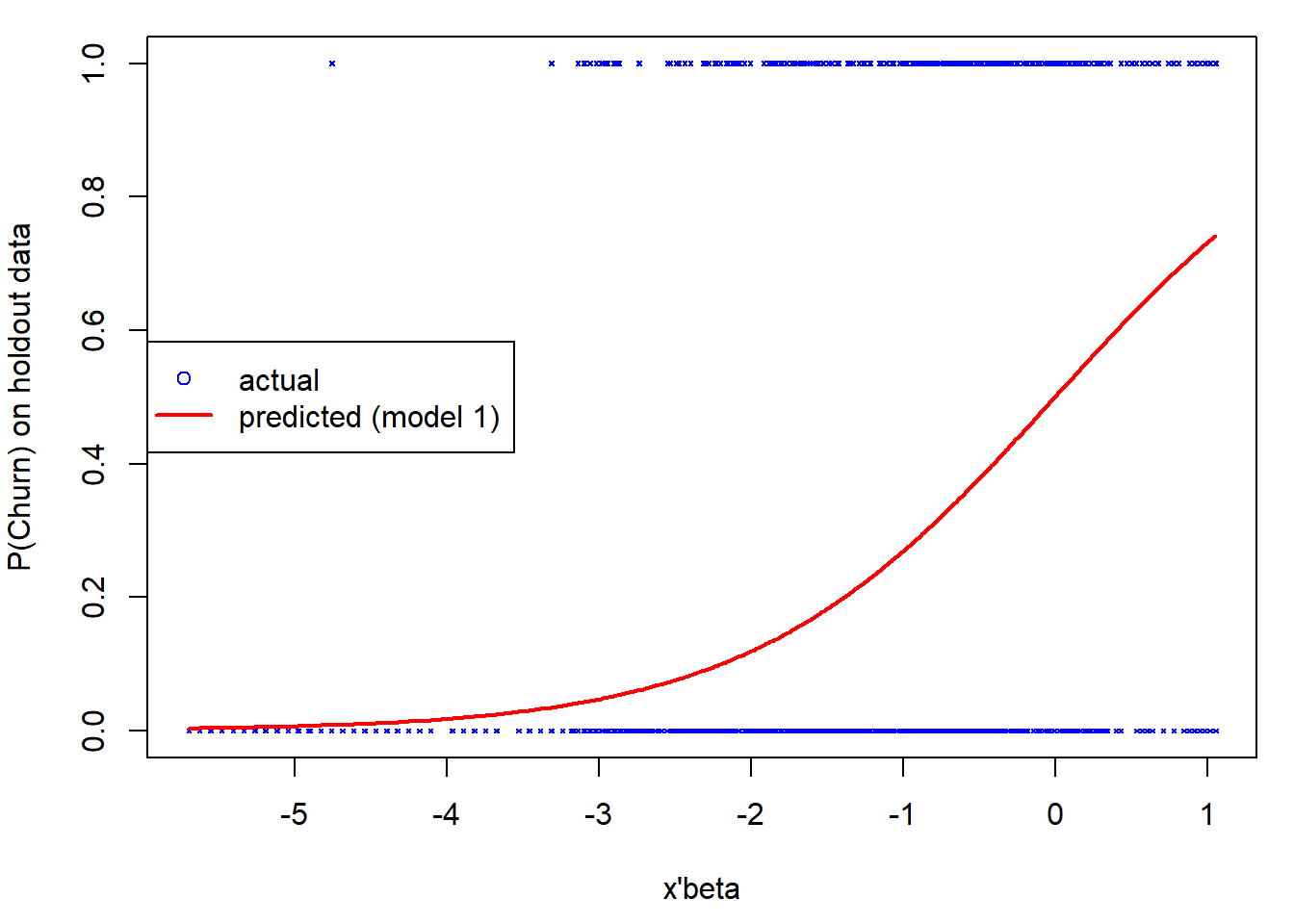
Question 6

What is the hit rate (Sensitivity) as a whole percentage?

Provide your answer with zero decimals without the percent sign (e.g. 120 or -120).

Confusion Matrix:

confusion_matrix <- (table(holdout_telco$Churn, prob > 0.5))
confusion_matrix <- as.data.frame.matrix(confusion_matrix)
colnames(confusion_matrix) <- c("No", "Yes")
confusion_matrix$Percentage_Correct <- confusion_matrix[1,]$No/(confusion_matrix[1,]$No+confusion_matrix[1,]$Yes)*100
confusion_matrix[2,]$Percentage_Correct <- confusion_matrix[2,]$Yes/(confusion_matrix[2,]$No+confusion_matrix[2,]$Yes)*100

print(confusion_matrix) %>% 
  kbl() %>%
  kable_styling()
##     No Yes Percentage_Correct
## 0 1393 120              92.07
## 1  353 217              38.07
No Yes Percentage_Correct
0 1393 120 92.07
1 353 217 38.07 
## Overall Percentage: 38 %

Question 7

If you target the top 2 deciles using Model 1 in the holdout data, what percentage of total churners would you have?

Provide your answer with zero decimals without the percent sign (e.g. 120 or -120).

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}
# create deciles
prob_decile = ntiles(prob, 10)

# prob, decile and actual
pred <- data.frame(cbind(prob,prob_decile, holdout_telco$Churn))
colnames(pred)<-c("predicted","decile", "actual")

# create lift table by decile
# average churn rate by decile

# lift is the actual churn rate in the decile divided by average overall churn rate
rbar_ho <- mean(holdout_telco$Churn)


lift_table <- pred %>% 
  group_by(decile) %>%  
  summarize(actual_churn = mean(actual), lift = actual_churn/rbar_ho, n_customers=n()) %>% 
  arrange(desc(decile)) %>% 
  mutate(cum_customers=cumsum(n_customers)) %>%
  mutate(cum_lift=cumsum(actual_churn)/sum(actual_churn)*100)
head(lift_table) %>% 
  kbl() %>%
  kable_styling()
decile actual_churn lift n_customers cum_customers cum_lift
10 0.6930 2.5326 215 215 25.43
9 0.5248 1.9176 202 417 44.69
8 0.4238 1.5488 210 627 60.24
7 0.3702 1.3528 208 835 73.83
6 0.2113 0.7721 213 1048 81.58
5 0.1238 0.4523 202 1250 86.13 
## [1] "Percentage of total churners: 44.69 %"
  • The top decile lift is 2.516. Customers in the top decile are 2.516 times more likely to actually churn than the average customer.
  • Targeting the top 20% using the model would give us 45% of total churners in the data.
pred <- pred %>% 
  arrange(desc(predicted)) %>% 
  mutate(prop_churn = cumsum(actual)/sum(actual)*100, 
         prop_cust = seq(nrow(pred))/nrow(pred)*100)
# Plotting percentage of churners as a function of percentage of customers
par(mai=c(.9,.8,.2,.2))
plot(pred$prop_cust, pred$prop_churn, 
     type="l", xlab="% of customers targeted using model", ylab="% of churners accounted for", xlim = c(0,100), ylim = c(0,100), col="blue")
legend('topleft', legend=c("Naive", "Logistic"), col=c("red", "blue"), lty=1:1, cex=0.8)
abline(a=0,b=1,col="red")
points(x=20, y= lift_table$cum_lift[2], pch=4, col="red",  cex=2, lwd=2)
text(x = 27.75,y= lift_table$cum_lift[2]+0.5, paste(round(lift_table$cum_lift[2],2), "%" ))

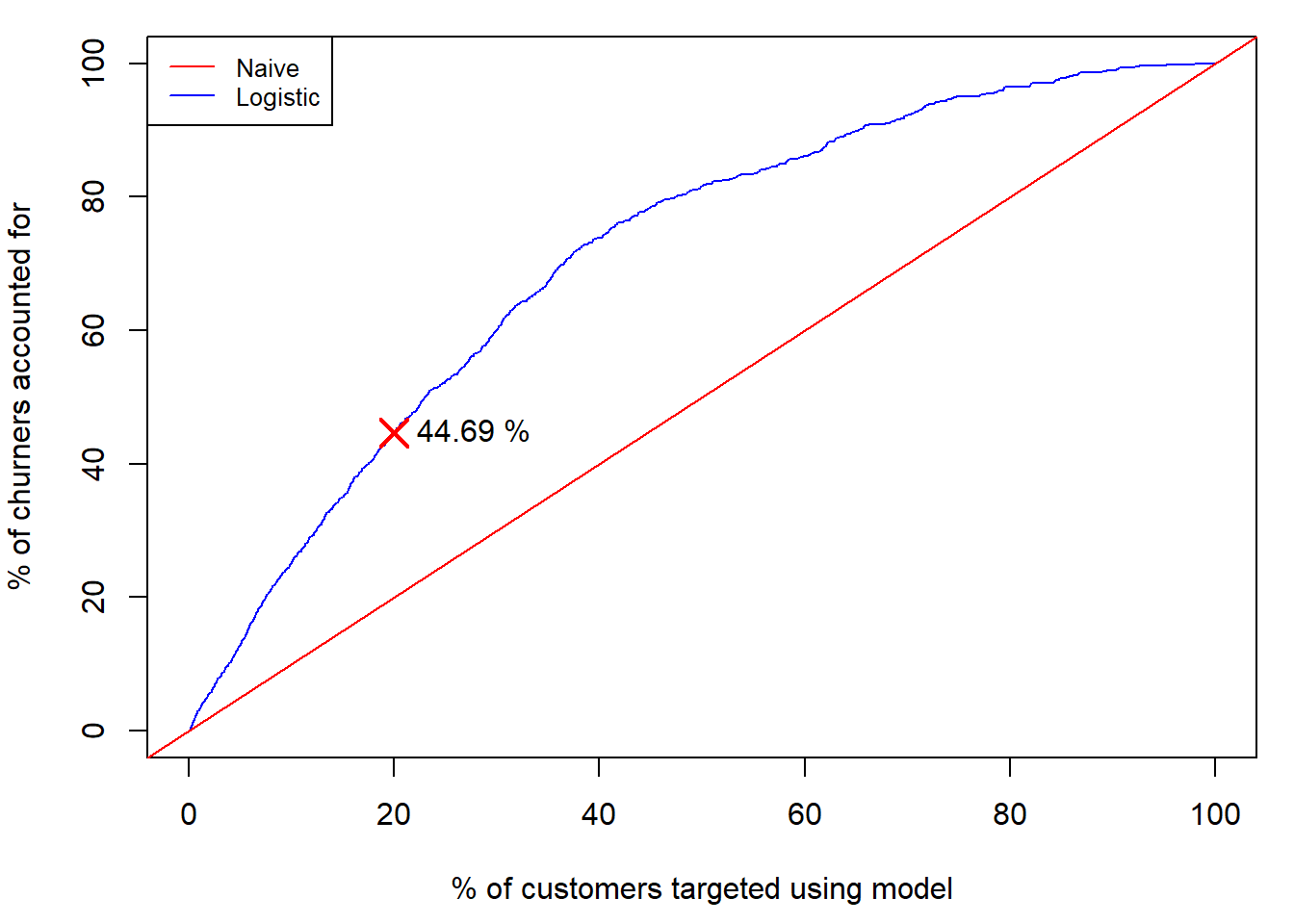
Question 8

How many deciles should you target to maximize expected profits, using the contact decision tree of Blattberg, Neslin and Kim?

Assume gamma = 0.1, LTV = 500, delta = 50, c = 0.50, psi = 1, and delta = 0.

Provide your answer (e.g. 0, 1, 2, … 10).

gamma = 0.1  # probability that customer is rescued if he or she is a churner
LTV = 500   # lifetime value of rescued customer
delta = 50  # cost of incentive
c = 0.50  # cost of contact

# re-order lift from highest to lowest
# add columns to our lift table

profit_table <- lift_table %>% 
  mutate(cum_prop_churners = cumsum(actual_churn*n_customers)/cum_customers, 
  profit = cum_customers*((gamma*LTV+delta*(1-gamma))*cum_prop_churners-delta-c),
  decile=11-decile)
## percentile number 2 with profits: $ 3166
par(mai=c(.9,.8,.2,.2))
bp <- barplot(profit_table$profit ~ profit_table$decile, main="expected profits by # of deciles targeted", xlab="# deciles targeted", ylab="expected profits")

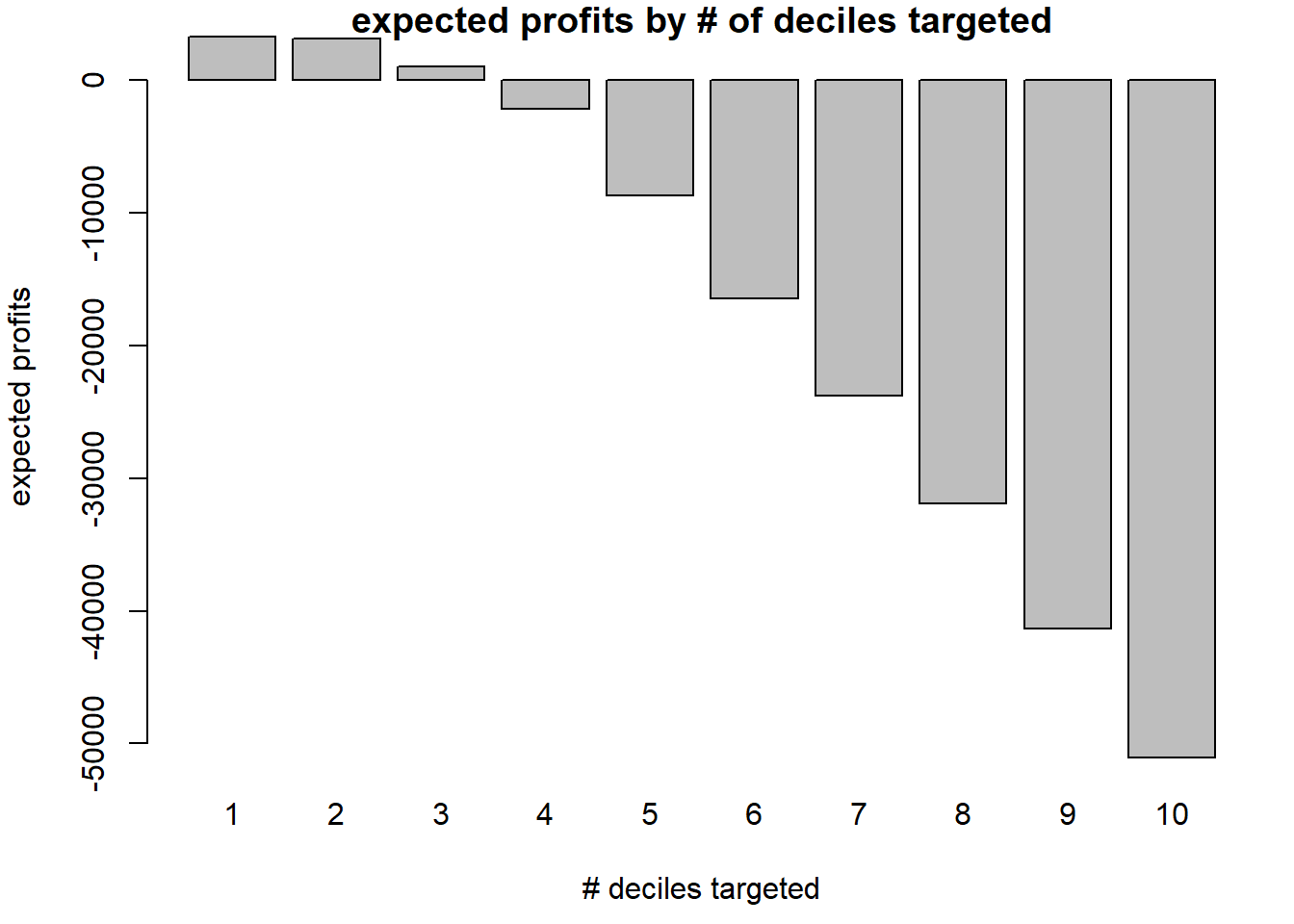
LS0tDQp0aXRsZTogIkFzc2lnbm1lbnQgMzogTG9naXN0aWMgUmVncmVzc2lvbiINCmF1dGhvcjogIkRhbmllbCBSZWRlbCINCmRhdGU6ICIyMDIyLTExLTExIg0Kb3V0cHV0OiANCiAgaHRtbF9kb2N1bWVudDoNCiAgICB0b2M6IFRSVUUNCiAgICB0b2NfZmxvYXQ6IFRSVUUNCiAgICBjb2RlX2Rvd25sb2FkOiBUUlVFDQotLS0NCg0KYGBge3Igc2V0dXAsIGluY2x1ZGU9RkFMU0V9DQpybShsaXN0ID0gbHMoKSkNCmxpYnJhcnkoY2FyKQ0KbGlicmFyeSh0aWR5dmVyc2UpDQpsaWJyYXJ5KHBST0MpDQpsaWJyYXJ5KHBsb3RyaXgpICAjIHBsb3R0aW5nIHdpdGggY29uZmlkZW5jZSBpbnRlcnZhbHMNCmxpYnJhcnkodGlkeXZlcnNlKQ0KbGlicmFyeShrYWJsZUV4dHJhKQ0Kb3B0aW9ucygic2NpcGVuIj0yMDAsICJkaWdpdHMiPTQpDQoNCmxpYnJhcnkocmVhZHIpDQpgYGANCg0KQSB0ZWxlY29tbXVuaWNhdGlvbnMgY29tcGFueSAobGlrZSBLUE4pIHdhbnRzIHRvIGltcGxlbWVudCBhIHByb2FjdGl2ZSBjaHVybiBwb2xpY3ksIHVzaW5nIGxvZ2lzdGljIHJlZ3Jlc3Npb24gdG8gcHJlZGljdCBjaHVybi4gVGhleSBhc3NlbWJsZSBhIGRhdGEgc2V0IG9mIHBhc3QgY3VzdG9tZXJzIHdobyBlaXRoZXIgY2h1cm5lZCBvciBzdGF5ZWQsIGFsb25nIHdpdGggc2V2ZXJhbCB2YXJpYWJsZXMgdGhhdCBjYW4gYmUgdXNlZCB0byBwcmVkaWN0IHRoaXMgZGVjaXNpb24uIFRoaXMgZGF0YSBzZXQgaXMgY2FsbGVkICp0ZWxjb190ZXN0LmNzdiouDQoNCmBgYHtyLCBtZXNzYWdlPUZBTFNFLCB3YXJuaW5nPUZBTFNFfQ0KdGVzdCA8LSByZWFkX2NzdigidGVsY29fdGVzdC5jc3YiKQ0KYGBgDQoNCk1ha2Ugc3VyZSBhbGwgbm9uLW1ldHJpYyB2YXJpYWJsZXMgbGlrZSBnZW5kZXIsIHNlbmlvciBjaXRpemVuLCBwYXJ0bmVyIGFyZSBjb2RlZCBhcyBhIGZhY3RvciAoYXMgZG9uZSBpbiB0aGUgbGFiIHNlc3Npb24pIGV4Y2VwdCBmb3IgMyB2YXJpYWJsZXMgLS0tIHRlbnVyZSwgbW9udGhseSBjaGFyZ2VzLCBhbmQgdG90YWwgY2hhcmdlcy4gVXNlIHRoaXMgY29kZToNCg0KYGBge3J9DQp0ZXN0JGdlbmRlciA8LSBhcy5mYWN0b3IodGVzdCRnZW5kZXIpDQp0ZXN0JFBheW1lbnRNZXRob2QgPC0gYXMuZmFjdG9yKHRlc3QkUGF5bWVudE1ldGhvZCkNCg0KIyBDaGFuZ2UgQ2h1cm4gZnJvbSAibm8iICJ5ZXMiIHRvIDAgMQ0KdGVzdCA8LSB0ZXN0ICU+JQ0KbXV0YXRlKENodXJuID0gaWZlbHNlKENodXJuID09ICJObyIsMCwxKSkNCmBgYA0KDQojIyBRdWVzdGlvbiAxDQoNCkxldCdzIGZvY3VzIG9uIHRoZSByZWxhdGlvbnNoaXAgYmV0d2VlbiBjaHVybiBhbmQgcGF5bWVudCBtZXRob2QgdXNpbmcganVzdCB0aGUgZGF0YS4NCg0KKipXaGF0IGlzIHRoZSBwcm9wb3J0aW9uIG9mIGNodXJuZXJzIG9mIHBlb3BsZSB3aG8gcGF5IHVzaW5nIGEgbWFpbGVkIGNoZWNrPyoqDQoNCipQcm92aWRlIHlvdXIgYW5zd2VyIHdpdGggdGhyZWUgZGVjaW1hbHMgc2VwYXJhdGVkIGJ5IGEgZG90LCBub3QgYSBjb21tYSAoZS5nLiAwLjEyMykqLg0KDQpgYGB7cn0NCm1haWxlZCA8LSB0ZXN0ICU+JSANCiAgZ3JvdXBfYnkoUGF5bWVudE1ldGhvZCkgJT4lIA0KICBzdW1tYXJpc2Uobj1uKCksIENodXJuID0gc3VtKENodXJuKSwgcF9jaHVybiA9IHJvdW5kKENodXJuL24sMykpDQoNCmBgYA0KDQpgYGB7ciwgZWNobz1GQUxTRX0NCmNhdCgiVGhlIHByb3BvcnRpb24gb2YgY2h1cm5lcnMgb2YgcGVvcGxlIHdobyBwYXkgdXNpbmcgYSBtYWlsZWQgY2hlY2sgaXMiLCBtYWlsZWQkcF9jaHVybls0XSkgIzAuMTg2DQpgYGANCg0KIyMgUXVlc3Rpb24gMg0KDQoqKldoYXQgaXMgdGhlIHVwcGVyIGJvdW5kIG9mIHRoZSA5NSUgY29uZmlkZW5jZSBpbnRlcnZhbCBmb3IgdGhlIHByb3BvcnRpb24gb2YgY2h1cm5lcnMgb2YgcGVvcGxlIHdobyBwYXkgdXNpbmcgYSBtYWlsZWQgY2hlY2s/KioNCg0KKlByb3ZpZGUgeW91ciBhbnN3ZXIgd2l0aCB0aHJlZSBkZWNpbWFscyBzZXBhcmF0ZWQgYnkgYSBkb3QsIG5vdCBhIGNvbW1hIChlLmcuIDAuMTIzKSouDQoNCmBgYHtyfQ0KY2h1cm5fcG1ldGhvZCA8LSB0ZXN0ICU+JSANCiAgZ3JvdXBfYnkoUGF5bWVudE1ldGhvZCkgJT4lIA0KICBzdW1tYXJpc2UocF9jaHVybiA9IG1lYW4oQ2h1cm4pLCANCiAgICAgICAgICAgIG5fY2h1cm5lcnMgPSBzdW0oQ2h1cm4pLCANCiAgICAgICAgICAgIG49bigpLA0KICAgICAgICAgICAgcF9jaHVybl9zZSA9IHNxcnQoKHBfY2h1cm4pKigxLXBfY2h1cm4pL24pKSAlPiUNCiAgbXV0YXRlKGxvd2VyX0NJX3BjaHVybiA9IHBfY2h1cm4gLSAxLjk2KnBfY2h1cm5fc2UsIA0KICAgICAgICAgdXBwZXJfQ0lfcGNodXJuID0gcF9jaHVybiArIDEuOTYqcF9jaHVybl9zZSkgDQoNCmNodXJuX3BtZXRob2QkdXBwZXJfQ0lfcGNodXJuWzRdICMjIDAuMjA5DQpgYGANCg0KUHJlZGljdCBjaHVybiB1c2luZyBnZW5kZXIsIHNlbmlvciBjaXRpemVuLCB0ZW51cmUgKGFzIGEgY29udGludW91cyB2YXJpYWJsZSksIHBheW1lbnQgbWV0aG9kLCBhbmQgdGhlIGludGVyYWN0aW9uIGJldHdlZW4gdGVudXJlIGFuZCBwYXltZW50IG1ldGhvZC4gQ2FsbCB0aGlzICoqbW9kZWwgMSoqLg0KDQpgYGB7ciBtb2RlbDB9DQojIGZpdCANCm1vZGVsXzEgPC0gZ2xtKENodXJuIH4gZ2VuZGVyICsgU2VuaW9yQ2l0aXplbiArIHRlbnVyZSpQYXltZW50TWV0aG9kLCBkYXRhPXRlc3QsIGZhbWlseSA9IGJpbm9taWFsKGxpbms9ImxvZ2l0IikpDQpgYGANCg0KIyMgUXVlc3Rpb24gMw0KDQoqKldoYXQgaXMgdGhlIFIyIG9mIG1vZGVsIDE/KioNCg0KKlByb3ZpZGUgeW91ciBhbnN3ZXIgd2l0aCB0aHJlZSBkZWNpbWFscyBzZXBhcmF0ZWQgYnkgYSBkb3QsIG5vdCBhIGNvbW1hIChlLmcuIDAuMTIzKSouDQoNCmBgYHtyfQ0KRCA8LSBtb2RlbF8xJGRldmlhbmNlICMgZ2V0IGRldmlhbmNlIEQgZm9yIGVhY2gNCkQwIDwtIG1vZGVsXzEkbnVsbC5kZXZpYW5jZSAjIERfMCBpcyB0aGUgc2FtZSBmb3IgYWxsIG1vZGVscw0KICANClIyIDwtIDEtRC9EMA0Kcm91bmQoUjIsMykNCmBgYA0KDQojIyBRdWVzdGlvbiA0DQoNCkFjY29yZGluZyB0byAqKm1vZGVsIDEqKiwgYSBjdXN0b21lciB3aG8gcGF5cyBieSBtYWlsZWQgY2hlY2sgaW5jcmVhc2VzIG9yIGRlY3JlYXNlcyBoaXMgb3IgaGVyIGxpa2VsaWhvb2Qgb2YgY2h1cm4gd2l0aCBlYWNoIHVuaXQgaW5jcmVhc2UgaW4gdGVudXJlLg0KDQoqKlJlcG9ydCB0aGUgb2RkcyBmb3IgdGhpcyBjdXN0b21lcioqDQoNCipQcm92aWRlIHlvdXIgYW5zd2VyIHdpdGggemVybyBkZWNpbWFscyB3aXRob3V0IHRoZSBwZXJjZW50IHNpZ24gKGUuZy4gMTIwIG9yIC0xMjApKi4NCg0KYGBge3J9DQpjb2VmMSA8LSByb3VuZCggKGV4cChjb2VmKG1vZGVsXzEpWyJ0ZW51cmUiXSArIGNvZWYobW9kZWxfMSlbInRlbnVyZTpQYXltZW50TWV0aG9kTWFpbGVkIGNoZWNrIl0pLTEgKSoxMDAsIDApDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQpjYXQoIk9kZHMgRGVjcmVhc2VzIiwgY29lZjEsIiUiKQ0KYGBgDQoNClRoZSBvZGRzIG9mIGEgY3VzdG9tZXIgd2hvIHBheXMgYnkgbWFpbGVkIGNoZWNrIGFuZCBpbmNyZWFzZSB0ZW51cmUgYnkgYW4gdW5pdCB2cyAiaGFzIGEgdGVudXJlIG9mIDEiIGFyZSBkaWZmZXJlbnQuDQoNCiMjIFF1ZXN0aW9uIDUNCg0KKipXaGF0IGlzIHRoZSBLLWZvbGQgY3Jvc3MgdmFsaWRhdGlvbiBlc3RpbWF0ZSBvZiBSMj8qKg0KDQpVc2UgSyA9IDUsIHNldCB0aGUgc2VlZCB0byAxOTEwMy4gUmVwb3J0IHRoZSBhdmVyYWdlIG9mIHRoZSB2YWx1ZXMuDQoNCipQcm92aWRlIHlvdXIgYW5zd2VyIHdpdGggdHdvIGRlY2ltYWxzIHNlcGFyYXRlZCBieSBhIGRvdCwgbm90IGEgY29tbWEgKGUuZy4gMC4xMikqLg0KDQpgYGB7ciwgY2FjaGU9VFJVRX0NCnNldC5zZWVkKDE5MTAzKQ0KbiA9IG5yb3codGVzdCkNCksgPSA1ICMgIyBmb2xkcw0KZm9sZGlkID0gcmVwKDE6SywgZWFjaD1jZWlsaW5nKG4vSykpW3NhbXBsZSgxOm4pXQ0KT09TIDwtIGRhdGEuZnJhbWUobW9kZWwxPXJlcChOQSxLKSkNCg0KDQojIyBwcmVkIG11c3QgYmUgcHJvYmFiaWxpdGllcyAoMDxwcmVkPDEpIGZvciBiaW5vbWlhbA0KICBkZXZpYW5jZSA8LSBmdW5jdGlvbih5LCBwcmVkLCBmYW1pbHk9YygiZ2F1c3NpYW4iLCJiaW5vbWlhbCIpKXsNCiAgICBmYW1pbHkgPC0gbWF0Y2guYXJnKGZhbWlseSkNCiAgICBpZihmYW1pbHk9PSJnYXVzc2lhbiIpew0KICAgICAgcmV0dXJuKCBzdW0oICh5LXByZWQpXjIgKSApDQogICAgfWVsc2V7DQogICAgICBpZihpcy5mYWN0b3IoeSkpIHkgPC0gYXMubnVtZXJpYyh5KT4xDQogICAgICByZXR1cm4oIC0yKnN1bSggeSpsb2cocHJlZCkgKyAoMS15KSpsb2coMS1wcmVkKSApICkNCiAgICB9DQogIH0NCg0KIyMgZ2V0IG51bGwgZGV2aWFuY2UgdG9vLCBhbmQgcmV0dXJuIFIyDQogIFIyIDwtIGZ1bmN0aW9uKHksIHByZWQsIGZhbWlseT1jKCJnYXVzc2lhbiIsImJpbm9taWFsIikpew0KICBmYW0gPC0gbWF0Y2guYXJnKGZhbWlseSkNCiAgaWYoZmFtPT0iYmlub21pYWwiKXsNCiAgICBpZihpcy5mYWN0b3IoeSkpeyB5IDwtIGFzLm51bWVyaWMoeSk+MSB9DQogIH0NCiAgZGV2IDwtIGRldmlhbmNlKHksIHByZWQsIGZhbWlseT1mYW0pDQogIGRldjAgPC0gZGV2aWFuY2UoeSwgbWVhbih5KSwgZmFtaWx5PWZhbSkNCiAgcmV0dXJuKDEtZGV2L2RldjApDQogIH0gIA0KDQojIHRoaXMgcGFydCB3aWxsIHRha2Ugc2V2ZXJhbCBtaW51dGVzLCBmaXR0aW5nIDMgbW9kZWxzIEsgdGltZXMgZWFjaA0KICANCmZvcihrIGluIDE6Syl7DQogIHRyYWluID0gd2hpY2goZm9sZGlkIT1rKSAjIGRhdGEgdXNlZCB0byB0cmFpbg0KICANCiAgIyBmaXQgcmVncmVzc2lvbnMNCiAgbW9kZWxfMSA8LSBnbG0oQ2h1cm4gfiBnZW5kZXIgKyBTZW5pb3JDaXRpemVuICsgdGVudXJlKlBheW1lbnRNZXRob2QsIGRhdGE9dGVzdFt0cmFpbixdLCBmYW1pbHkgPSBiaW5vbWlhbChsaW5rPSJsb2dpdCIpKQ0KICANCiAgIyBwcmVkaWN0IG9uIGhvbGRvdXQgZGF0YSAoLXRyYWluKQ0KICBwcmVkMSA8LSBwcmVkaWN0KG1vZGVsXzEsIG5ld2RhdGE9dGVzdFstdHJhaW4sXSwgdHlwZSA9ICJyZXNwb25zZSIpICMjVFJBSU4gREFUQSBub3QsIHRoZSBXSE9MRSBTQU1QTEUNCiAgDQogICMgY2FsY3VsYXRlIFIyDQogIE9PUyRtb2RlbDFba10gPC0gUjIoeSA9IHRlc3QkQ2h1cm5bLXRyYWluXSxwcmVkPXByZWQxLCBmYW1pbHk9ImJpbm9taWFsIikNCiAgDQogICMgcHJpbnQgcHJvZ3Jlc3MNCiAgY2F0KGssICIgICIpDQogICAgDQp9DQogIA0KYGBgDQoNCmBgYHtyLCBlY2hvPUZBTFNFfQ0KY2F0KCJBdmVyYWdlIG9mIFIyIGlzIiwgcm91bmQobWVhbihPT1MkbW9kZWwxKSwyKSAgKQ0KYGBgDQoNCmBgYHtyfQ0KcGFyKG1haT1jKC45LC44LC4yLC4yKSkgIA0KYm94cGxvdChPT1NbLDFdLCBkYXRhPU9PUywgbWFpbj1leHByZXNzaW9uKHBhc3RlKCJPdXQtb2YtU2FtcGxlIFIiXiIyIikpLA0KICAgICAgICB4bGFiPSJNb2RlbCIsIHlsYWI9ZXhwcmVzc2lvbihwYXN0ZSgiUiJeIjIiKSkpDQpgYGANCg0KQXBwbHkgKiptb2RlbCAxKiogdG8gdGhlIGhvbGRvdXQgZGF0YSBzZXQsICp0ZWxjb19ob2xkb3V0LmNzdiouDQoNCmBgYHtyLCBtZXNzYWdlPUZBTFNFLCB3YXJuaW5nPUZBTFNFfQ0KaG9sZG91dF90ZWxjbyA8LSByZWFkX2NzdigidGVsY29faG9sZG91dC5jc3YiKQ0KDQojIyBEdW1tZXM6DQpob2xkb3V0X3RlbGNvJGdlbmRlcjwtYXMuZmFjdG9yKGhvbGRvdXRfdGVsY28kZ2VuZGVyKQ0KaG9sZG91dF90ZWxjbyRQYXltZW50TWV0aG9kPC1hcy5mYWN0b3IoaG9sZG91dF90ZWxjbyRQYXltZW50TWV0aG9kKQ0KDQojIENoYW5nZSBDaHVybiBmcm9tICJubyIgInllcyIgdG8gMCAxDQpob2xkb3V0X3RlbGNvIDwtIGhvbGRvdXRfdGVsY28gJT4lDQogIG11dGF0ZShDaHVybiA9IGlmZWxzZShDaHVybiA9PSAiTm8iLDAsMSkpDQpgYGANCg0KUHJlZGljdGluZyBDaHVybmluZzoNCg0KYGBge3J9DQojIHByZWRpY3RlZCB4J2JldGEgcGFydCBvZiANCnhiIDwtIHByZWRpY3QobW9kZWxfMSwgdHlwZSA9ICJsaW5rIiwgbmV3ZGF0YT1ob2xkb3V0X3RlbGNvKQ0KIyB0aGUgcHJlZGljdGVkIHByb2JhYmlsaXR5IA0KcHJvYiA8LSBwcmVkaWN0KG1vZGVsXzEsIHR5cGUgPSAicmVzcG9uc2UiLCBuZXdkYXRhPWhvbGRvdXRfdGVsY28pDQoNCmhlYWQoY2JpbmQoeGIscHJvYikpICU+JSANCiAga2JsKCkgJT4lDQogIGthYmxlX3N0eWxpbmcoKQ0KYGBgDQoNClBsb3Q6DQoNCmBgYHtyfQ0KIyBmaXJzdCB3ZSBhcnJhbmdlOg0KaW5kIDwtIG9yZGVyKHByb2IpDQoNCiMjIFBMT1QNCnBhcihtYWk9YyguOSwuOCwuMiwuMikpDQpwbG90KHhiW2luZF0saG9sZG91dF90ZWxjbyRDaHVybltpbmRdLCBwY2g9NCxjZXg9MC4zLGNvbD0iYmx1ZSIsIHhsYWI9IngnYmV0YSIseWxhYj0iUChDaHVybikgb24gaG9sZG91dCBkYXRhIikNCmxpbmVzKHg9eGJbaW5kXSwgeT1wcm9iW2luZF0sIGNvbD0icmVkIiwgbHdkPTIpDQpsZWdlbmQoJ2xlZnQnLGxlZ2VuZD1jKCJhY3R1YWwiLCAicHJlZGljdGVkIChtb2RlbCAxKSIpLGNvbD1jKCJibHVlIiwicmVkIiksIHBjaD1jKDEsTkEpLGx0eT1jKE5BLDEpLCBsd2Q9YyhOQSwyKSkNCmBgYA0KDQojIyBRdWVzdGlvbiA2DQoNCioqV2hhdCBpcyB0aGUgaGl0IHJhdGUgKFNlbnNpdGl2aXR5KSBhcyBhIHdob2xlIHBlcmNlbnRhZ2U/KioNCg0KKlByb3ZpZGUgeW91ciBhbnN3ZXIgd2l0aCB6ZXJvIGRlY2ltYWxzIHdpdGhvdXQgdGhlIHBlcmNlbnQgc2lnbiAoZS5nLiAxMjAgb3IgLTEyMCkqLg0KDQpbKipDb25mdXNpb24gTWF0cml4Kipdey51bmRlcmxpbmV9Og0KDQpgYGB7cn0NCmNvbmZ1c2lvbl9tYXRyaXggPC0gKHRhYmxlKGhvbGRvdXRfdGVsY28kQ2h1cm4sIHByb2IgPiAwLjUpKQ0KY29uZnVzaW9uX21hdHJpeCA8LSBhcy5kYXRhLmZyYW1lLm1hdHJpeChjb25mdXNpb25fbWF0cml4KQ0KY29sbmFtZXMoY29uZnVzaW9uX21hdHJpeCkgPC0gYygiTm8iLCAiWWVzIikNCmNvbmZ1c2lvbl9tYXRyaXgkUGVyY2VudGFnZV9Db3JyZWN0IDwtIGNvbmZ1c2lvbl9tYXRyaXhbMSxdJE5vLyhjb25mdXNpb25fbWF0cml4WzEsXSRObytjb25mdXNpb25fbWF0cml4WzEsXSRZZXMpKjEwMA0KY29uZnVzaW9uX21hdHJpeFsyLF0kUGVyY2VudGFnZV9Db3JyZWN0IDwtIGNvbmZ1c2lvbl9tYXRyaXhbMixdJFllcy8oY29uZnVzaW9uX21hdHJpeFsyLF0kTm8rY29uZnVzaW9uX21hdHJpeFsyLF0kWWVzKSoxMDANCg0KcHJpbnQoY29uZnVzaW9uX21hdHJpeCkgJT4lIA0KICBrYmwoKSAlPiUNCiAga2FibGVfc3R5bGluZygpDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQpjYXQoJ092ZXJhbGwgUGVyY2VudGFnZTonLCAocm91bmQoY29uZnVzaW9uX21hdHJpeFsyLDJdLyhjb25mdXNpb25fbWF0cml4WzIsMl0rY29uZnVzaW9uX21hdHJpeFsyLDFdKSoxMDAsMCkpLCAiJSIpDQpgYGANCg0KIyMgUXVlc3Rpb24gNw0KDQoqKklmIHlvdSB0YXJnZXQgdGhlIHRvcCAyIGRlY2lsZXMgdXNpbmcgTW9kZWwgMSBpbiB0aGUgaG9sZG91dCBkYXRhLCB3aGF0IHBlcmNlbnRhZ2Ugb2YgdG90YWwgY2h1cm5lcnMgd291bGQgeW91IGhhdmU/KioNCg0KKlByb3ZpZGUgeW91ciBhbnN3ZXIgd2l0aCB6ZXJvIGRlY2ltYWxzIHdpdGhvdXQgdGhlIHBlcmNlbnQgc2lnbiAoZS5nLiAxMjAgb3IgLTEyMCkqLg0KDQpgYGB7cn0NCm50aWxlcyA8LSBmdW5jdGlvbih4LCBiaW5zKSB7DQogIHF1YW50aWxlcyA9IHNlcShmcm9tPTAsIHRvID0gMSwgbGVuZ3RoLm91dD1iaW5zKzEpDQogIGN1dChlY2RmKHgpKHgpLGJyZWFrcz1xdWFudGlsZXMsIGxhYmVscz1GKQ0KfQ0KIyBjcmVhdGUgZGVjaWxlcw0KcHJvYl9kZWNpbGUgPSBudGlsZXMocHJvYiwgMTApDQoNCiMgcHJvYiwgZGVjaWxlIGFuZCBhY3R1YWwNCnByZWQgPC0gZGF0YS5mcmFtZShjYmluZChwcm9iLHByb2JfZGVjaWxlLCBob2xkb3V0X3RlbGNvJENodXJuKSkNCmNvbG5hbWVzKHByZWQpPC1jKCJwcmVkaWN0ZWQiLCJkZWNpbGUiLCAiYWN0dWFsIikNCg0KIyBjcmVhdGUgbGlmdCB0YWJsZSBieSBkZWNpbGUNCiMgYXZlcmFnZSBjaHVybiByYXRlIGJ5IGRlY2lsZQ0KDQojIGxpZnQgaXMgdGhlIGFjdHVhbCBjaHVybiByYXRlIGluIHRoZSBkZWNpbGUgZGl2aWRlZCBieSBhdmVyYWdlIG92ZXJhbGwgY2h1cm4gcmF0ZQ0KcmJhcl9obyA8LSBtZWFuKGhvbGRvdXRfdGVsY28kQ2h1cm4pDQoNCg0KbGlmdF90YWJsZSA8LSBwcmVkICU+JSANCiAgZ3JvdXBfYnkoZGVjaWxlKSAlPiUgIA0KICBzdW1tYXJpemUoYWN0dWFsX2NodXJuID0gbWVhbihhY3R1YWwpLCBsaWZ0ID0gYWN0dWFsX2NodXJuL3JiYXJfaG8sIG5fY3VzdG9tZXJzPW4oKSkgJT4lIA0KICBhcnJhbmdlKGRlc2MoZGVjaWxlKSkgJT4lIA0KICBtdXRhdGUoY3VtX2N1c3RvbWVycz1jdW1zdW0obl9jdXN0b21lcnMpKSAlPiUNCiAgbXV0YXRlKGN1bV9saWZ0PWN1bXN1bShhY3R1YWxfY2h1cm4pL3N1bShhY3R1YWxfY2h1cm4pKjEwMCkNCg0KYGBgDQoNCmBgYHtyfQ0KaGVhZChsaWZ0X3RhYmxlKSAlPiUgDQogIGtibCgpICU+JQ0KICBrYWJsZV9zdHlsaW5nKCkNCmBgYA0KDQpgYGB7ciwgZWNobz1GQUxTRX0NCnBhc3RlKCJQZXJjZW50YWdlIG9mIHRvdGFsIGNodXJuZXJzOiIsIHJvdW5kKGxpZnRfdGFibGUkY3VtX2xpZnRbMl0sMiksICIlIiApICMjIEFuc3dlcg0KYGBgDQoNCi0gICBUaGUgdG9wIGRlY2lsZSBsaWZ0IGlzIDIuNTE2LiBDdXN0b21lcnMgaW4gdGhlIHRvcCBkZWNpbGUgYXJlIDIuNTE2IHRpbWVzIG1vcmUgbGlrZWx5IHRvIGFjdHVhbGx5IGNodXJuIHRoYW4gdGhlIGF2ZXJhZ2UgY3VzdG9tZXIuDQotICAgVGFyZ2V0aW5nIHRoZSB0b3AgMjAlIHVzaW5nIHRoZSBtb2RlbCB3b3VsZCBnaXZlIHVzIDQ1JSBvZiB0b3RhbCBjaHVybmVycyBpbiB0aGUgZGF0YS4NCg0KYGBge3J9DQpwcmVkIDwtIHByZWQgJT4lIA0KICBhcnJhbmdlKGRlc2MocHJlZGljdGVkKSkgJT4lIA0KICBtdXRhdGUocHJvcF9jaHVybiA9IGN1bXN1bShhY3R1YWwpL3N1bShhY3R1YWwpKjEwMCwgDQogICAgICAgICBwcm9wX2N1c3QgPSBzZXEobnJvdyhwcmVkKSkvbnJvdyhwcmVkKSoxMDApDQpgYGANCg0KYGBge3J9DQojIFBsb3R0aW5nIHBlcmNlbnRhZ2Ugb2YgY2h1cm5lcnMgYXMgYSBmdW5jdGlvbiBvZiBwZXJjZW50YWdlIG9mIGN1c3RvbWVycw0KcGFyKG1haT1jKC45LC44LC4yLC4yKSkNCnBsb3QocHJlZCRwcm9wX2N1c3QsIHByZWQkcHJvcF9jaHVybiwgDQogICAgIHR5cGU9ImwiLCB4bGFiPSIlIG9mIGN1c3RvbWVycyB0YXJnZXRlZCB1c2luZyBtb2RlbCIsIHlsYWI9IiUgb2YgY2h1cm5lcnMgYWNjb3VudGVkIGZvciIsIHhsaW0gPSBjKDAsMTAwKSwgeWxpbSA9IGMoMCwxMDApLCBjb2w9ImJsdWUiKQ0KbGVnZW5kKCd0b3BsZWZ0JywgbGVnZW5kPWMoIk5haXZlIiwgIkxvZ2lzdGljIiksIGNvbD1jKCJyZWQiLCAiYmx1ZSIpLCBsdHk9MToxLCBjZXg9MC44KQ0KYWJsaW5lKGE9MCxiPTEsY29sPSJyZWQiKQ0KcG9pbnRzKHg9MjAsIHk9IGxpZnRfdGFibGUkY3VtX2xpZnRbMl0sIHBjaD00LCBjb2w9InJlZCIsICBjZXg9MiwgbHdkPTIpDQp0ZXh0KHggPSAyNy43NSx5PSBsaWZ0X3RhYmxlJGN1bV9saWZ0WzJdKzAuNSwgcGFzdGUocm91bmQobGlmdF90YWJsZSRjdW1fbGlmdFsyXSwyKSwgIiUiICkpDQpgYGANCg0KIyMgUXVlc3Rpb24gOA0KDQoqKkhvdyBtYW55IGRlY2lsZXMgc2hvdWxkIHlvdSB0YXJnZXQgdG8gbWF4aW1pemUgZXhwZWN0ZWQgcHJvZml0cywgdXNpbmcgdGhlIGNvbnRhY3QgZGVjaXNpb24gdHJlZSBvZiBCbGF0dGJlcmcsIE5lc2xpbiBhbmQgS2ltPyoqDQoNCkFzc3VtZSBnYW1tYSA9IDAuMSwgTFRWID0gNTAwLCBkZWx0YSA9IDUwLCBjID0gMC41MCwgcHNpID0gMSwgYW5kIGRlbHRhID0gMC4NCg0KKlByb3ZpZGUgeW91ciBhbnN3ZXIgKGUuZy4gMCwgMSwgMiwgLi4uIDEwKSouDQoNCmBgYHtyfQ0KZ2FtbWEgPSAwLjEgICMgcHJvYmFiaWxpdHkgdGhhdCBjdXN0b21lciBpcyByZXNjdWVkIGlmIGhlIG9yIHNoZSBpcyBhIGNodXJuZXINCkxUViA9IDUwMCAgICMgbGlmZXRpbWUgdmFsdWUgb2YgcmVzY3VlZCBjdXN0b21lcg0KZGVsdGEgPSA1MCAgIyBjb3N0IG9mIGluY2VudGl2ZQ0KYyA9IDAuNTAgICMgY29zdCBvZiBjb250YWN0DQoNCiMgcmUtb3JkZXIgbGlmdCBmcm9tIGhpZ2hlc3QgdG8gbG93ZXN0DQojIGFkZCBjb2x1bW5zIHRvIG91ciBsaWZ0IHRhYmxlDQoNCnByb2ZpdF90YWJsZSA8LSBsaWZ0X3RhYmxlICU+JSANCiAgbXV0YXRlKGN1bV9wcm9wX2NodXJuZXJzID0gY3Vtc3VtKGFjdHVhbF9jaHVybipuX2N1c3RvbWVycykvY3VtX2N1c3RvbWVycywgDQogIHByb2ZpdCA9IGN1bV9jdXN0b21lcnMqKChnYW1tYSpMVFYrZGVsdGEqKDEtZ2FtbWEpKSpjdW1fcHJvcF9jaHVybmVycy1kZWx0YS1jKSwNCiAgZGVjaWxlPTExLWRlY2lsZSkNCmBgYA0KDQpgYGB7ciwgZWNobz1GQUxTRX0NCmNhdCgicGVyY2VudGlsZSBudW1iZXIiLCBwcm9maXRfdGFibGUkZGVjaWxlWzJdLCAid2l0aCBwcm9maXRzOiAkIiwgcHJvZml0X3RhYmxlJHByb2ZpdFsyXSkNCmBgYA0KDQpgYGB7cn0NCnBhcihtYWk9YyguOSwuOCwuMiwuMikpDQpicCA8LSBiYXJwbG90KHByb2ZpdF90YWJsZSRwcm9maXQgfiBwcm9maXRfdGFibGUkZGVjaWxlLCBtYWluPSJleHBlY3RlZCBwcm9maXRzIGJ5ICMgb2YgZGVjaWxlcyB0YXJnZXRlZCIsIHhsYWI9IiMgZGVjaWxlcyB0YXJnZXRlZCIsIHlsYWI9ImV4cGVjdGVkIHByb2ZpdHMiKQ0KYGBgDQo=