Quiz 2: RFM Analysis

Question 1

A company is considering using RFM segments to target its rollout. The mailing under consideration costs €0.50 to send; if customers respond, they spend on average €50, of which €15 is margin.

It conducted a test of customers in the file, ebeer_test.csv; the customers not in the test can be found in ebeer_rollout.csv. For this analysis, create 3 RFM groups (instead of 5 like we did in class). 

What is the average recency of the group that is most recent, i.e., the customers who purchased most recently? 

Provide your answer with one decimal separated by a dot, not a comma (e.g. 0.1).

ebeer_test$Rgroup <- quantcut(ebeer_test$R, q = 3)

Alternatively:

# Create Quantiles 
ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x), breaks = quantiles, labels=F)
}
ebeer_test$Rgroup <- ntiles(ebeer_test$R, bins=3)  

recency_stats <- ebeer_test %>% 
  group_by(Rgroup) %>% 
  summarise(n = n(), 
            mean_R = mean(R), sd_R = sd(R), 
            resp_p = mean(respmail, na.rm=TRUE))
recency_stats %>% 
  kbl() %>%
  kable_styling()

Rgroup	n	mean_R	sd_R	resp_p
1	756	5.01	2.27	0.122
2	926	11.94	1.66	0.132
3	847	22.64	6.94	0.131

## The Average Recency of Group [2:10] is 5

Question 2

What is the response probability of that group? 

Provide your answer with two decimals separated by a dot, not a comma (e.g. 0.17).

## The Response Rate of Group [2:10] is 0.12

Question 3

Now do the full RFM analysis. 

How many RFM groups are there?

Provide your answer with zero decimals (e.g. 17).

The Code:

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}

ebeer_test$Rgroup <- ntiles(ebeer_test$R, bins=3)  


dt = data.table(ebeer_test)
nbins = 3
dt[, RFgroup := paste0(as.character(Rgroup), as.character(ntiles(F, bins = nbins))), by = c('Rgroup')]
dt[, RFMgroup := paste0(as.character(RFgroup), as.character(ntiles(M, bins = nbins))), by = c('RFgroup')]

# put it back to data.frame
ebeer_test = data.frame(dt)

# change it to a factor variable
ebeer_test$RFMgroup<-as.factor(ebeer_test$RFMgroup)

Number of RFM Groups:

length(unique(ebeer_test$RFMgroup))

## [1] 27

Question 4

How many of these segments are profitable to send to? 

Provide your answer with zero decimals (e.g. 12).

Let’s calculate the response rates for each segment:

respRFM <- ebeer_test %>% 
  group_by(RFMgroup) %>% 
  summarise(n_resp= sum(respmail, na.rm = TRUE), 
            n_mail= sum(mailing, na.rm = TRUE)) %>% 
  mutate(resp_rate = n_resp/n_mail) %>% 
  arrange(desc(resp_rate))
head(respRFM) %>% 
  kbl() %>%
  kable_styling()

RFMgroup	n_resp	n_mail	resp_rate
331	37	101	0.366
232	40	111	0.360
231	33	111	0.297
132	28	96	0.292
333	30	103	0.291
332	28	103	0.272

Breakeven Point:

c <- 0.5
m <- 15
brk <- c/m

How many to target?:

sum(respRFM$resp_rate >= brk)

## [1] 17

respRFM <- as.data.frame(respRFM)

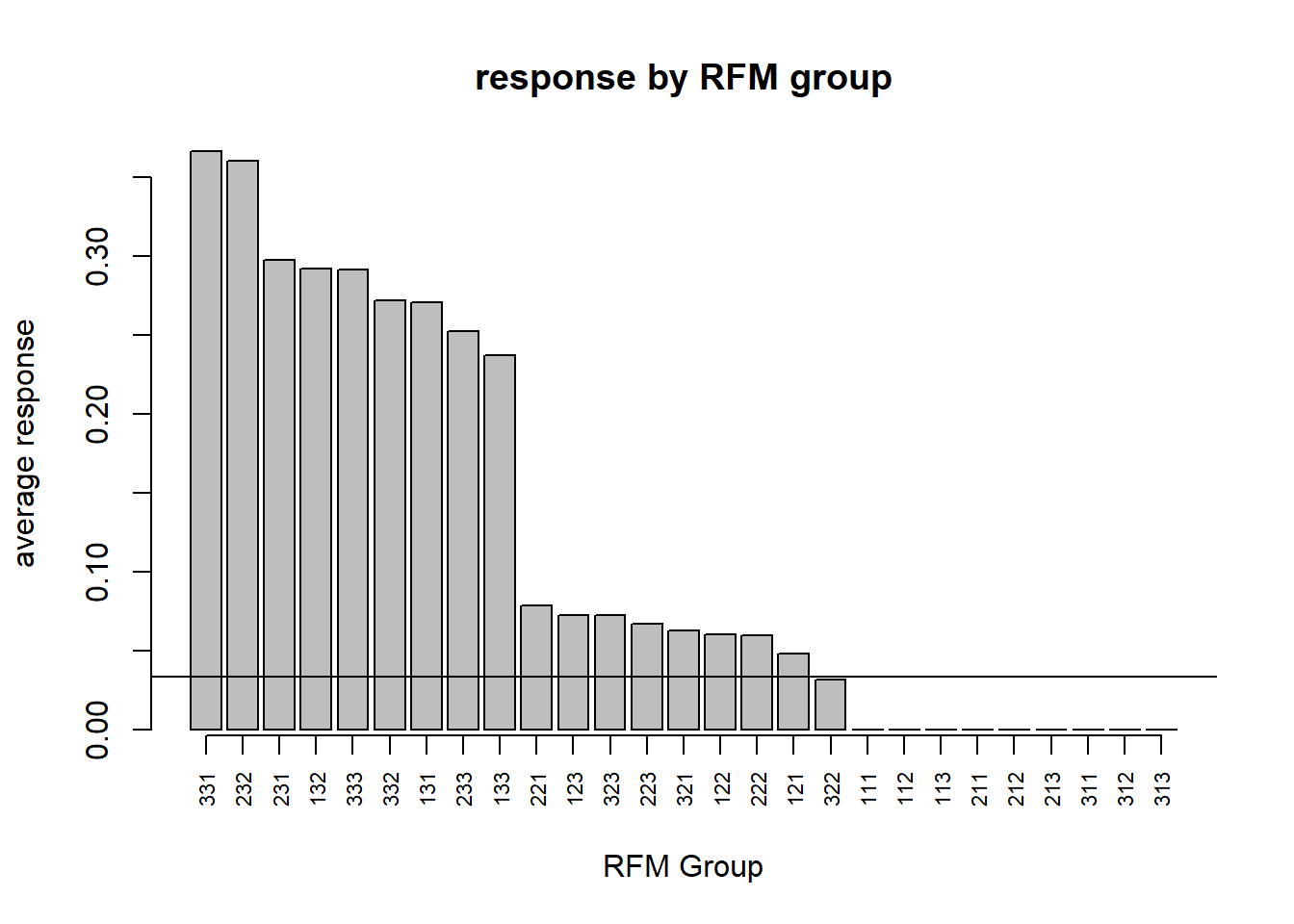
bp <- barplot(respRFM[,4], 
              main="response by RFM group", 
              xlab="RFM Group", ylab="average response", xaxt="n")
axis(1, at = bp[,1], labels=respRFM[,1], cex.axis=0.7, las=2)

abline(h=brk)
text(85, brk, "breakeven", cex=1, pos=3, col="black")

Question 5

What fraction of total variation in responses is explained by the RFM model? 

Provide your answer with three decimals separated by a dot, not a comma (e.g. 0.127)

RFM_model <- lm(respmail ~ RFMgroup, data = ebeer_test)
round(summary(RFM_model)$r.squared,3)

## [1] 0.153

Question 6

How many customers in the roll-out sample should be targeted? 

Provide your answer with zero decimals (e.g. 12).

Let’s consider now the roll-out data. We need first to create the segments:

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}

ebeer_rollout$Rgroup <- ntiles(ebeer_rollout$R, bins=3)  


dt = data.table(ebeer_rollout)
nbins = 3
dt[, RFgroup := paste0(as.character(Rgroup), as.character(ntiles(F, bins = nbins))), by = c('Rgroup')]
dt[, RFMgroup := paste0(as.character(RFgroup), as.character(ntiles(M, bins = nbins))), by = c('RFgroup')]

# put it back to data.frame
ebeer_rollout = data.frame(dt)

# change it to a factor variable
ebeer_rollout$RFMgroup<-as.factor(ebeer_rollout$RFMgroup)

We want to predict their response rates:

ebeer_rollout$RFMpred <- predict(RFM_model, ebeer_rollout)
sum(ebeer_rollout$RFMpred >= brk)

## [1] 1564

rollout_respRFM <- ebeer_rollout %>% 
  group_by(RFMgroup) %>% 
  summarise(n_resp= sum(respmail, na.rm = TRUE), 
            n_mail= sum(mailing, na.rm = TRUE)) %>% 
  mutate(resp_rate = n_resp/n_mail) %>% 
  arrange(desc(resp_rate))

rollout_respRFM <- as.data.frame(rollout_respRFM)

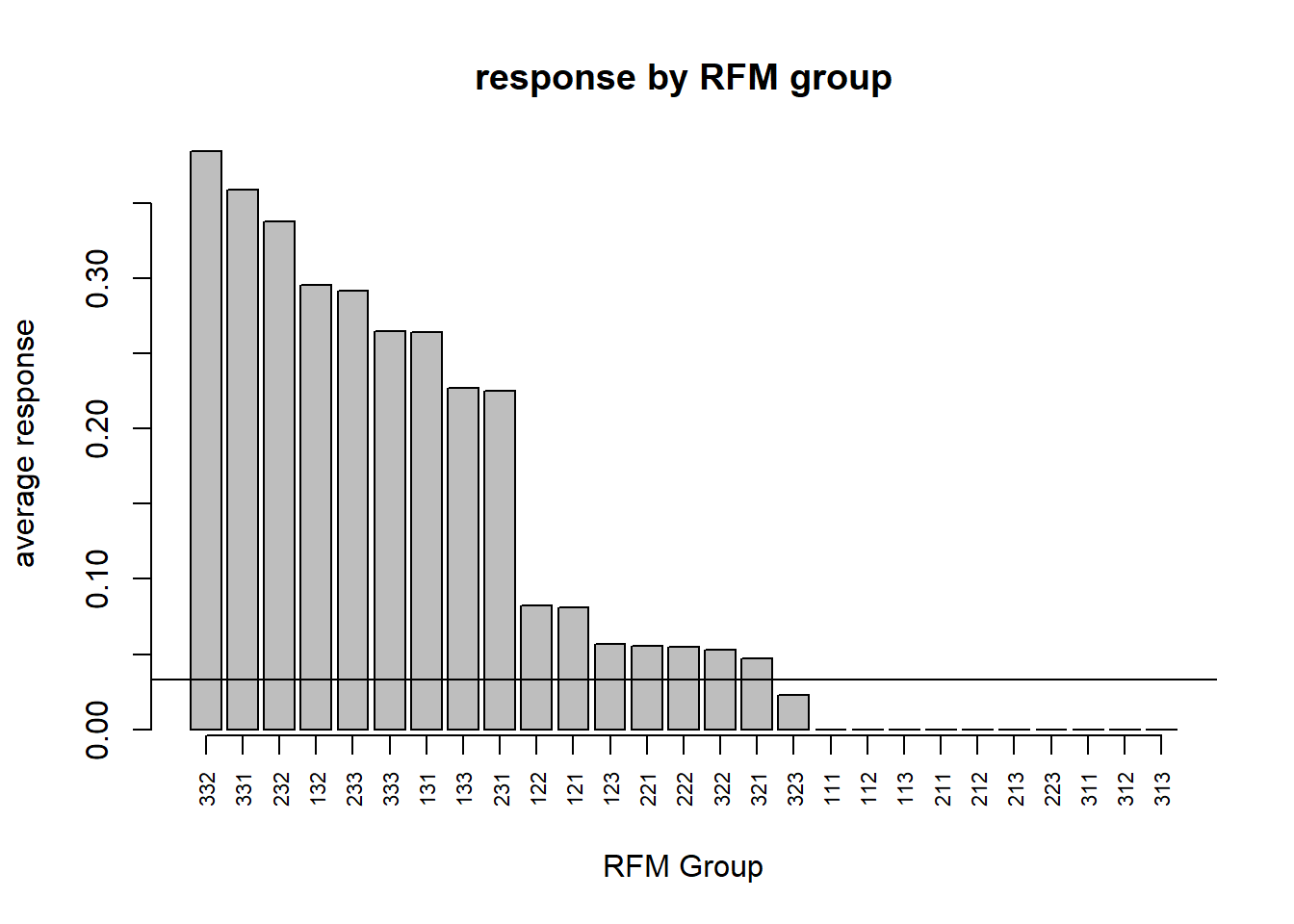
bp <- barplot(rollout_respRFM[,4], 
              main="response by RFM group", 
              xlab="RFM Group", ylab="average response", xaxt="n")
axis(1, at = bp[,1], labels=rollout_respRFM[,1], cex.axis=0.7, las=2)

abline(h=brk)
text(85, brk, "breakeven", cex=1, pos=3, col="black")

Question 7

What is the return on investment of rolling out to those segments? 

Provide your answer with zero decimals without the percent sign (e.g. 120).

Profit per Consumer:

ebeer_rollout <- ebeer_rollout %>% 
    mutate(RFMprofit = case_when(RFMpred >= brk ~ RFMpred*m-c, TRUE ~ 0))

Sum of Profits:

sum_profit <- sum(ebeer_rollout$RFMprofit)
sum_profit

## [1] 3592

Costs per Consumer:

ebeer_rollout <- ebeer_rollout %>% 
    mutate(RFMcost = case_when(RFMpred >= brk ~ c, TRUE ~ 0))

Sum of Costs:

sum_cost <- sum(ebeer_rollout$RFMcost)
sum_cost 

## [1] 782

ROI:

## The ROI is 459 %

Question 8

Use a beta-binomial model to shrink the segment estimates in the test data.  

How many extra segments would you target using this method that you wouldn’t otherwise target?

Provide your answer with zero decimals (e.g. 12).

First, we need the non-response data:

respRFM <- respRFM %>% 
  mutate(n_nonresp = n_mail-n_resp) %>% 
  relocate(n_nonresp, .after=n_resp)

Likelihood Function to fit the data and find prior response rate:

fit <- vglm(cbind(respRFM$n_resp,respRFM$n_nonresp) ~ 1, betabinomialff, trace=TRUE)

## VGLM    linear loop  1 :  loglikelihood = -87.958729
## VGLM    linear loop  2 :  loglikelihood = -87.944974
## VGLM    linear loop  3 :  loglikelihood = -87.944815
## VGLM    linear loop  4 :  loglikelihood = -87.944812
## VGLM    linear loop  5 :  loglikelihood = -87.944812

a <- Coef(fit)[[1]]
b <- Coef(fit)[[2]]

## (a,b)=( 0.388 , 3.11 )

We know can estimate the posterior response rates:

post_mean_resp <- (a+respRFM$n_resp)/(a+b+respRFM$n_mail)
respRFM <- cbind(respRFM, post_mean_resp)

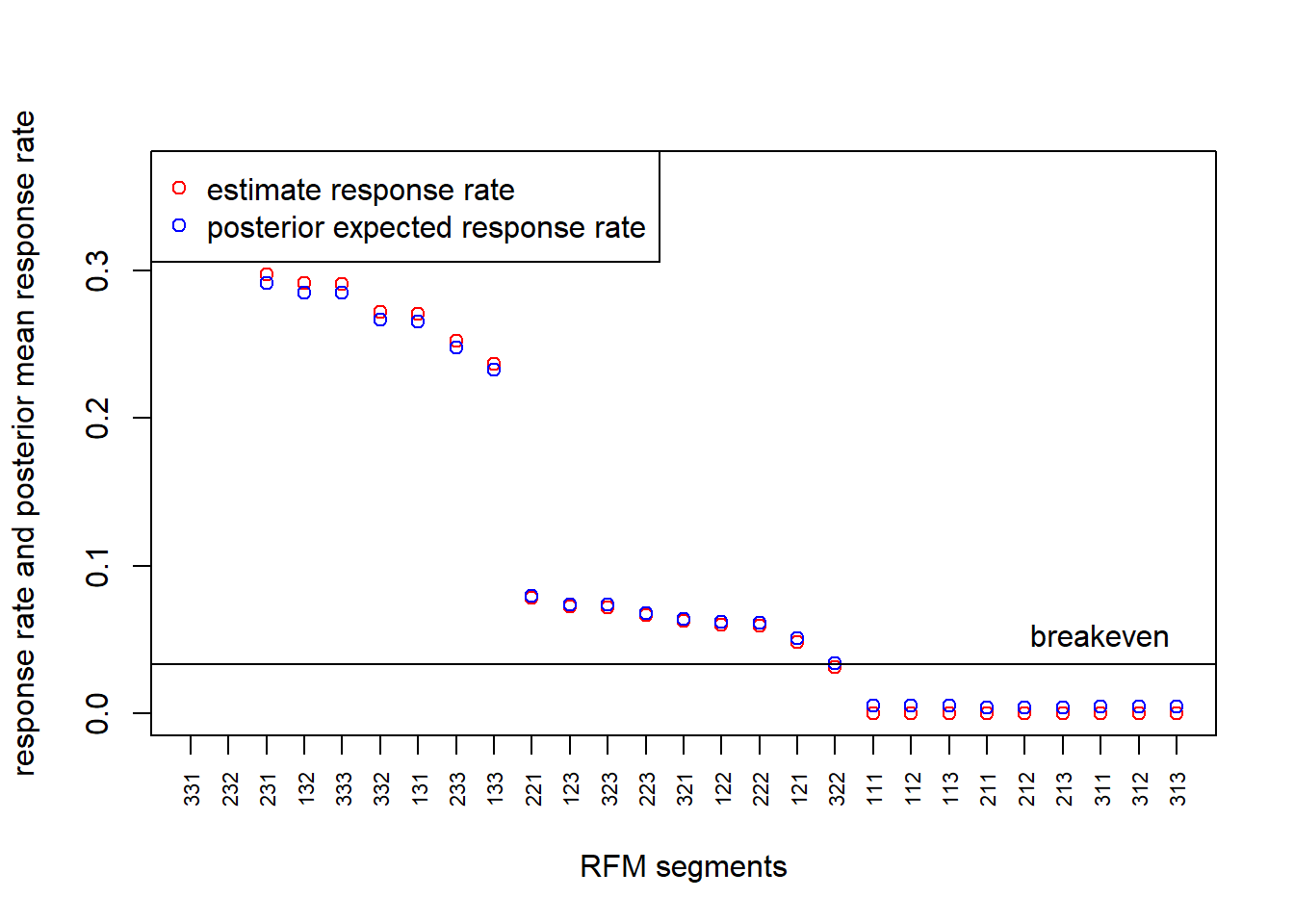
plot(respRFM$resp_rate, xaxt="n",col="red",xlab="RFM segments",ylab="response rate and posterior mean response rate")
points(respRFM$post_mean_resp, col='blue')
legend('topleft',legend=c("estimate response rate", "posterior expected response rate"),col=c("red","blue"), pch=1)
axis(1, at = 1:27, labels=respRFM$RFMgroup, cex.axis=0.7, las=2)
abline(h=brk)
text(25, brk, "breakeven", cex=1, pos=3, col="black")

In the end, how many extra segments should we target?

sum(respRFM$post_mean_resp >= brk) - sum(respRFM$resp_rate >= brk)

## [1] 1