Quiz 3: Logistics Regression

Question 1

A telecommunications company (like KPN) wants to implement a proactive churn policy, using logistic regression to predict churn. They assemble a data set of past customers who either churned or stayed, along with several variables that can be used to predict this decision. This data set is called telco_test.csv.

test <- read_csv("test.csv")

Make sure all non-metric variables like gender, senior citizen, partner are coded as a factor (as done in the lab session) except for 3 variables — tenure, monthly charges, and total charges. Use this code:

test$gender <- as.factor(test$gender)
test$SeniorCitizen <- as.factor(test$SeniorCitizen)
test$Partner <- as.factor(test$Partner)
test$PaymentMethod <- as.factor(test$PaymentMethod)

# Change Churn from "no" "yes" to 0 1
test <- test %>%
mutate(Churn = ifelse(Churn == "No",0,1))

Predict churn using gender, senior citizen, and tenure (as a continuous variable). There should be 4 coefficients estimated.

According to this model, what is the probability that a male senior who has been a customer for one month churns? 

Provide your answer with two decimals separated by a dot, not a comma (e.g. 0.17).

First, we fit the model:

model_1 <- glm(Churn ~ gender + SeniorCitizen + tenure, data=test, family = binomial(link="logit"))

We now make the prediction:

new <- data.frame(gender="Male", SeniorCitizen=as.factor(1), tenure=1)
pred <- predict(model_1, newdata = new, type = "response")

## The churn probability of a male senior who has been a customer for one month is 0.7

Question 2

Gender and senior citizen status may interact to create a different effect on churn. Add an interaction term to the model so that now there are 5 coefficients estimated in total.

What is the probability that a male senior with 1-month tenure churns?

Provide your answer with two decimals separated by a dot, not a comma (e.g. 0.17).

Model 2:

model_2 <- glm(Churn ~ gender*SeniorCitizen + tenure, data=test, family = binomial(link="logit"))

The Churn Probability of a male senior with 1-month tenure:

new <- data.frame(gender="Male", SeniorCitizen=as.factor(1), tenure=1)
pred <- predict(model_2, newdata = new, type = "response")

## The churn probability of a male senior with one month of tenure is 0.71

Question 3

Predict churn using all variables. There should be 24 coefficients estimated.

What’s the R² of this model?

Provide your answer with two decimals separated by a dot, not a comma (e.g. 0.17).

Model 3:

model_3 <- glm(Churn ~ ., data=test, family = binomial(link="logit"))

R-Squared by hand:

D <- model_3$deviance
D0 <- model_3$null.deviance
R2 <- 1-D/D0
round(R2,2)

## [1] 0.29

Question 4

Now instead of treating tenure as continuous, we are going to create 3 groups — low, medium, and high — from it (Hint: use ntiles).

Make sure it is a factor variable. Estimate a model now with tenure group instead of tenure. There should be 25 coefficients estimated.

How much more or less likely are customers in the high tenure group to churn relative to the low tenure group? Report the percentage change in odds rounded to the nearest whole percentage.

Provide your answer with zero decimals and without a percent sign (e.g. 17 or -17).

We start by creating the 3-tiles:

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}

## Tenure: 3 groups called "tenure_group"
test$tenure_group <- ntiles(test$tenure, bins=3)  
test$tenure_group <- as.factor(test$tenure_group)

Model 4:

test1 <- test %>% select(-tenure)
model_4 <- glm(Churn ~ ., data=test1, family = binomial(link="logit"))

Model Interpretation: The lowest tenure group is omitted or absorved by the intercept:

round((exp(coef(model_4)["tenure_group3"])-1)*100,0)

## tenure_group3 
##           -55

Question 5

Apply this model (model 4) to the holdout data set, telco_holdout.csv.

telco_holdout <- read_csv("telco_holdout.csv")

We create factor variables:

telco_holdout$gender <- as.factor(telco_holdout$gender)
telco_holdout$SeniorCitizen <- as.factor(telco_holdout$SeniorCitizen)
telco_holdout$Partner <- as.factor(telco_holdout$Partner)
telco_holdout$PaymentMethod <- as.factor(telco_holdout$PaymentMethod)

# Change Churn from "no" "yes" to 0 1
telco_holdout <- telco_holdout %>%
mutate(Churn = ifelse(Churn == "No",0,1))

# DO NOT FORGET THE 3 GROUPS
telco_holdout$tenure_group <- ntiles(telco_holdout$tenure, bins=3)  
telco_holdout$tenure_group <- as.factor(telco_holdout$tenure_group)

What is the hit rate, i.e., the true positive rate, as a whole percentage? 

Provide your answer with zero decimals and without a percent sign (e.g. 17 or -17).

# Predicted x'beta
xb <- predict(model_4, newdata = telco_holdout, type="link")
# Predicted probability
prob <- predict(model_4, newdata = telco_holdout, type="response")
# re-order
ind <- order(prob)

Confusion Matrix:

confusion_matrix <- (table(telco_holdout$Churn, prob > 0.5))
confusion_matrix <- as.data.frame.matrix(confusion_matrix)

colnames(confusion_matrix) <- c("No", "Yes")

confusion_matrix$Percentage_Correct <- confusion_matrix[1,]$No/(confusion_matrix[1,]$No+confusion_matrix[1,]$Yes)*100
confusion_matrix[2,]$Percentage_Correct <- confusion_matrix[2,]$Yes/(confusion_matrix[2,]$No+confusion_matrix[2,]$Yes)*100
print(confusion_matrix)

##     No Yes Percentage_Correct
## 0 1371 142              90.61
## 1  282 288              50.53

cat('Hit Rate:', round((confusion_matrix[2,2]/(confusion_matrix[2,1]+confusion_matrix[2,2]))*100),0)

## Hit Rate: 51 0

Question 6

Using this model to target the top 2 deciles would yield how many actual churners as a percentage of total churners?

Provide your answer with zero decimals and without a percent sign (e.g. 17 or -17).

We create the deciles:

# create deciles
prob_decile = ntiles(prob, 10)

# prob, decile and actual
pred <- data.frame(cbind(prob, prob_decile, telco_holdout$Churn))
colnames(pred)<-c("predicted","decile", "actual")

## create average churn
rbar_ho <- mean(telco_holdout$Churn)

We construct the lifts by decile:

lift_table <- pred %>% 
    group_by(decile) %>%  
    summarize(actual_churn = mean(actual), 
                        lift = actual_churn/rbar_ho, 
                        n_customers=n()) %>% 
    arrange(desc(decile)) %>% 
    mutate(cum_customers=cumsum(n_customers)) %>% 
    mutate(cum_lift=cumsum(actual_churn)/sum(actual_churn)*100)

head(lift_table) %>% 
  kbl() %>%
  kable_styling()

decile	actual_churn	lift	n_customers	cum_customers	cum_lift
10	0.7560	2.7626	209	209	27.64
9	0.6058	2.2137	208	417	49.79
8	0.4423	1.6164	208	625	65.97
7	0.2919	1.0666	209	834	76.64
6	0.2548	0.9312	208	1042	85.96
5	0.1827	0.6676	208	1250	92.64

Question 7

Let’s use the lift table to find the optimal number of top deciles to target, using the framework of BKN. Let’s assume the probability of being rescued if the person is actually a churner is 0.25, and the lifetime value of a customer is 250. The cost of the incentive is 30 and the cost of contact is 1. The rest of the parameters are the same as in the workbook.

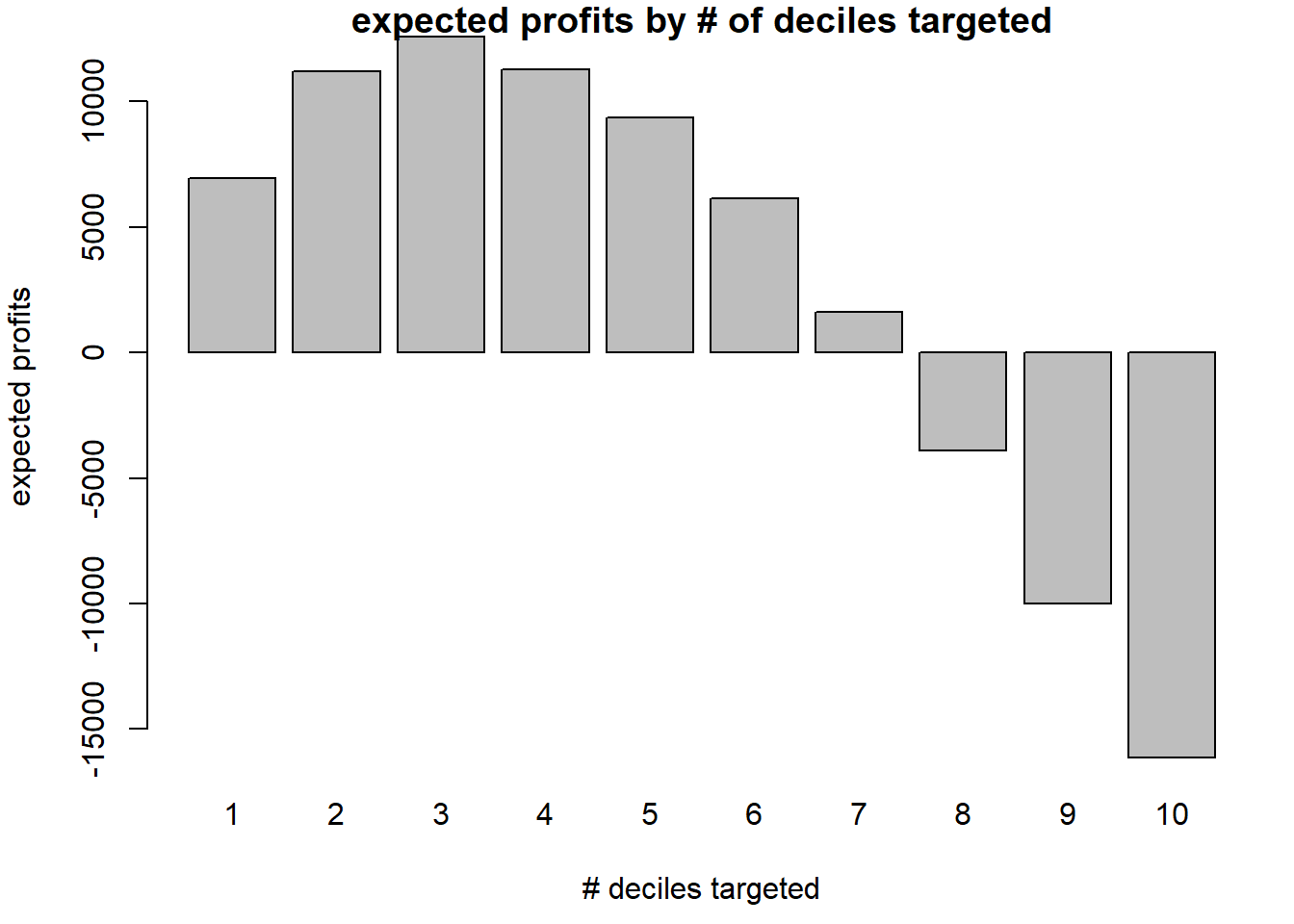
How many deciles would you target and what would be the expected profit ?

Provide your answer with zero decimals (e.g. 17000).

gamma = 0.25  # probability that customer is rescued if he or she is a churner
LTV = 250   # lifetime value of rescued customer
delta = 30  # cost of incentive
c = 1  # cost of contact

# re-order lift from highest to lowest
# add columns to our lift table

profit_table <- lift_table %>% mutate(
  cum_prop_churners = cumsum(actual_churn*n_customers)/cum_customers, 
  profit = cum_customers*((gamma*LTV+delta*(1-gamma))*cum_prop_churners-delta-c),
  decile=11-decile)

Figure:

par(mai=c(.9,.8,.2,.2))
bp<-barplot(profit_table$profit ~ profit_table$decile, main="expected profits by # of deciles targeted", xlab="# deciles targeted", ylab="expected profits")