Tutorial 6: CLV - Contractual Settings

Introduction

Customer Lifetime Value is the present value of the future profits associated with a particular customer. In this section, we’ll focus on contractual settings, where customers must notify the firm when they quit. In other words, customer churn is observed by the firm. The primitives of CLV are the margin, the discount rate, and retention, which often receives the most focus out of the three.

Basic Terms

Below we use some data from a subscription company. The time period is years.

active_cust=c(12489,
7356,
5258,
4309,
3747,
3435,
3123,
2948,
2786,
2711,
2624)
data <- cbind(0:10,active_cust)
colnames(data)<-c("Period", "Active Customers")
data %>% 
  kbl() %>%
  kable_styling()

Period	Active Customers
0	12489
1	7356
2	5258
3	4309
4	3747
5	3435
6	3123
7	2948
8	2786
9	2711
10	2624

At year \(t=0\) there is a cohort of 12,489 customers who join in the same year.

A year later 7,356 of them renewed, so \(S(1) = \frac{7356}{12489} = 0.589\).

Coding hint: diff takes the difference between adjacent terms in a vector.

lost <- -diff(active_cust)
S <- active_cust[1:11]/active_cust[1] ## Survivor Function
data <- cbind(data, S)

data %>% 
  kbl() %>%
  kable_styling()

Period	Active Customers	S
0	12489	1.000
1	7356	0.589
2	5258	0.421
3	4309	0.345
4	3747	0.300
5	3435	0.275
6	3123	0.250
7	2948	0.236
8	2786	0.223
9	2711	0.217
10	2624	0.210

Survival Function Plot:

par(mai=c(.9,.8,.2,.2))

plot(0:10, S, type="b",ylab="Survival fucntion S(t)", xlab="Period",ylim=par("yaxp")[1:2]) 

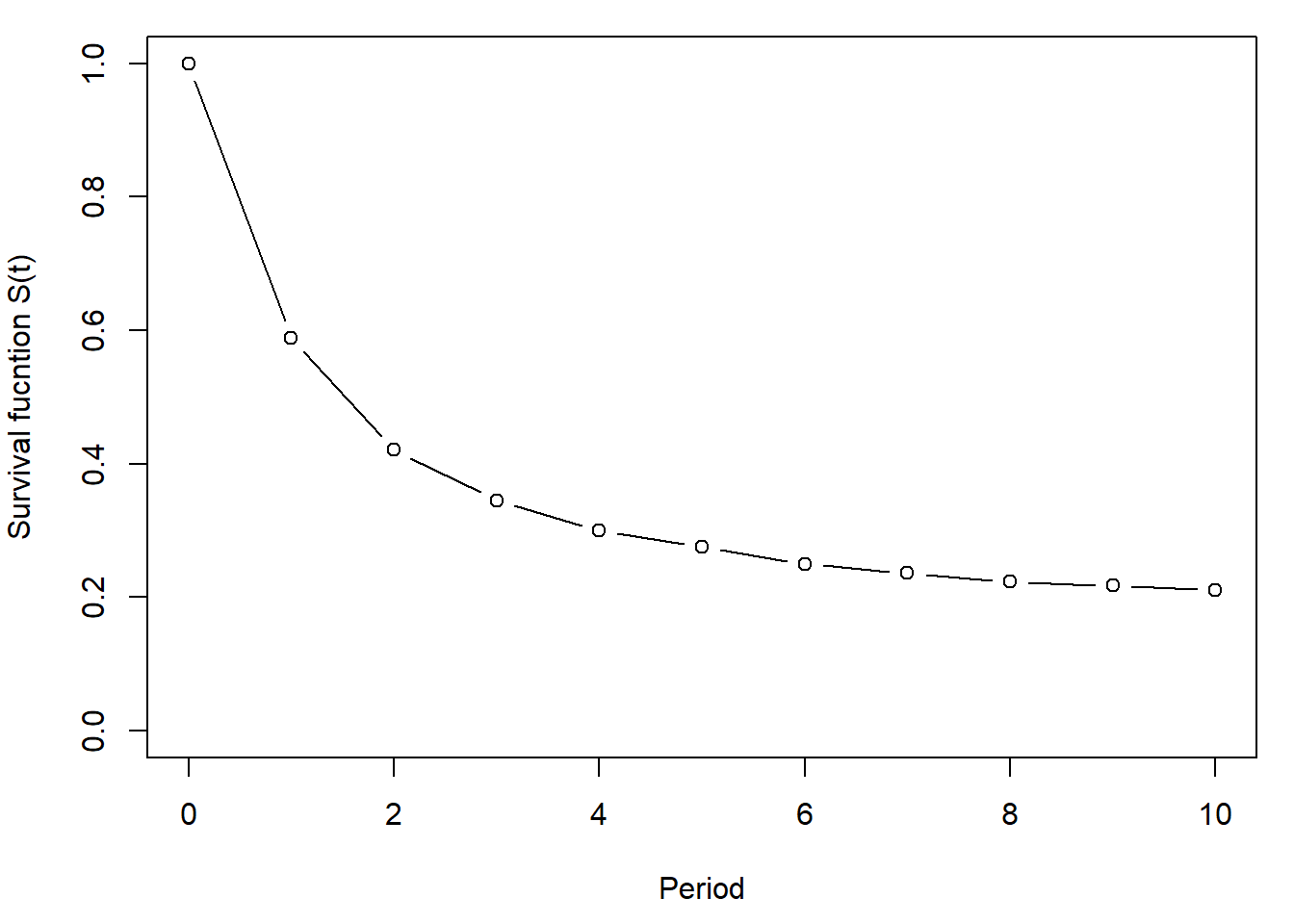
The retention rate is the probability that a customer who was active (i.e., still subscribed) in \(t-1\) will still be active at the end of the next period \(t\). This is a conditional probability, because we are conditioning on the fact that the customer has survived \(t-1\) periods.

It turns out the retention rate is the ratio of survivor functions in adjacent periods: \[ r(t) = P(T>t \mid T>t-1) = \frac{S(t)}{S(t-1)} \] In our data at \(t=2\), the retention rate is \(r(2) = \frac{5258}{7356} = 0.715\): of the 7356 customers who were active in \(t=1\), 5258 were active in \(t=2\).

r <- S[2:11]/S[1:10] # DEFINITION

data <- cbind(data, c(NA,r))
colnames(data)[[4]] <- "r"
data %>% 
  kbl() %>%
  kable_styling()

Period	Active Customers	S	r
0	12489	1.000	NA
1	7356	0.589	0.589
2	5258	0.421	0.715
3	4309	0.345	0.820
4	3747	0.300	0.870
5	3435	0.275	0.917
6	3123	0.250	0.909
7	2948	0.236	0.944
8	2786	0.223	0.945
9	2711	0.217	0.973
10	2624	0.210	0.968

Retention Rate Plot:

par(mai=c(.9,.8,.2,.2))
plot(1:10, r, type="b",ylab="retention rate r(t)", xlab="Period",ylim=par("yaxp")[1:2]) 

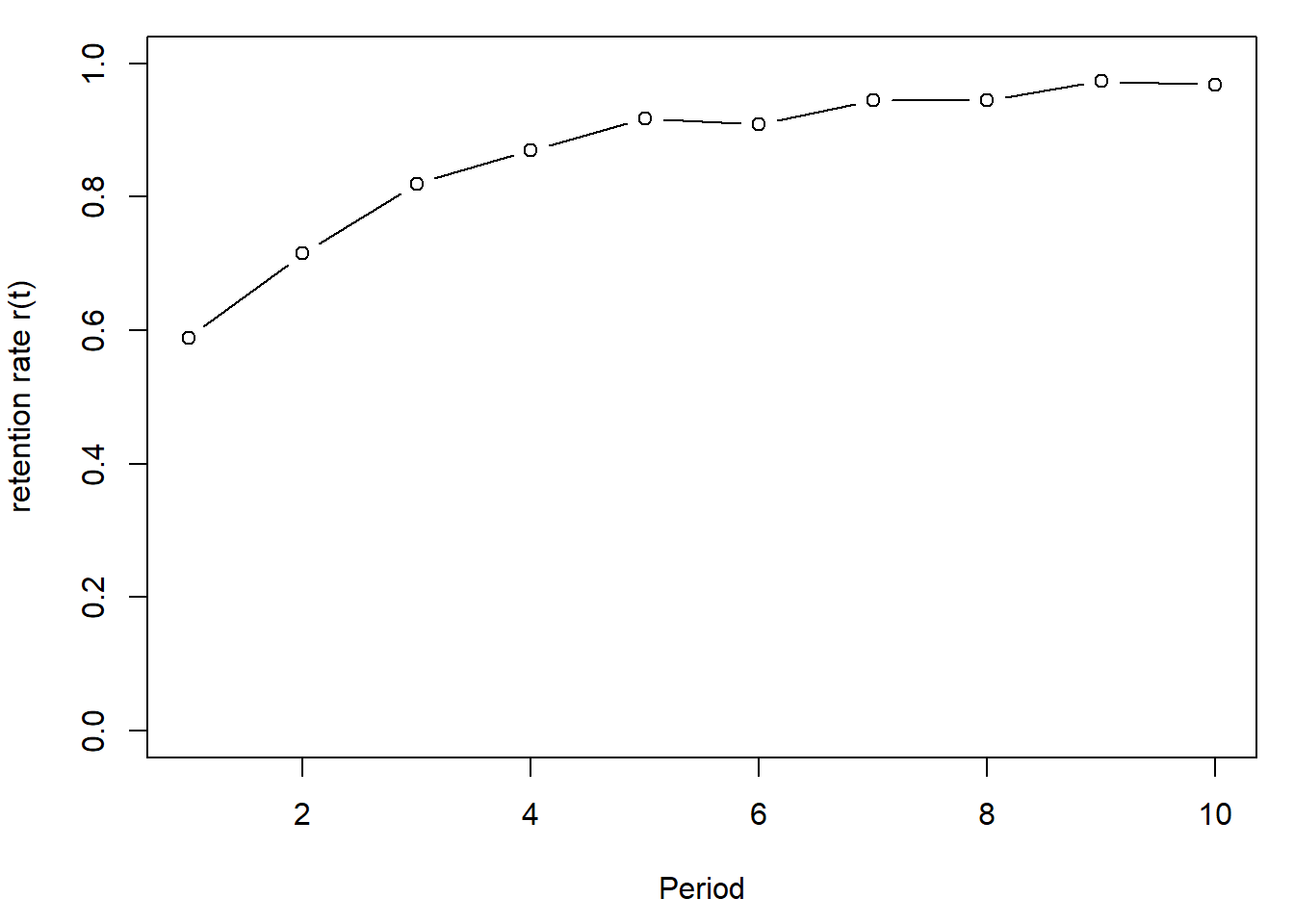
Lastly the churn rate is the probability that customer who was active in period \(t-1\) quits in period \(t\). Note this is related to the hazard rate, which is how social scientists model time until an event (here churn). It is the complement of the retention rate. In other words: \[ c(t)=P(T=t \mid T>t-1) = 1-r(t) \]

c <- 1-r
data <- cbind(data, c(NA,c))
colnames(data)[[5]] <- "c"

par(mai=c(.9,.8,.2,.2))
plot(1:10, c, type="b",ylab="churn rate c(t)", xlab="Period",ylim=par("yaxp")[1:2]) 

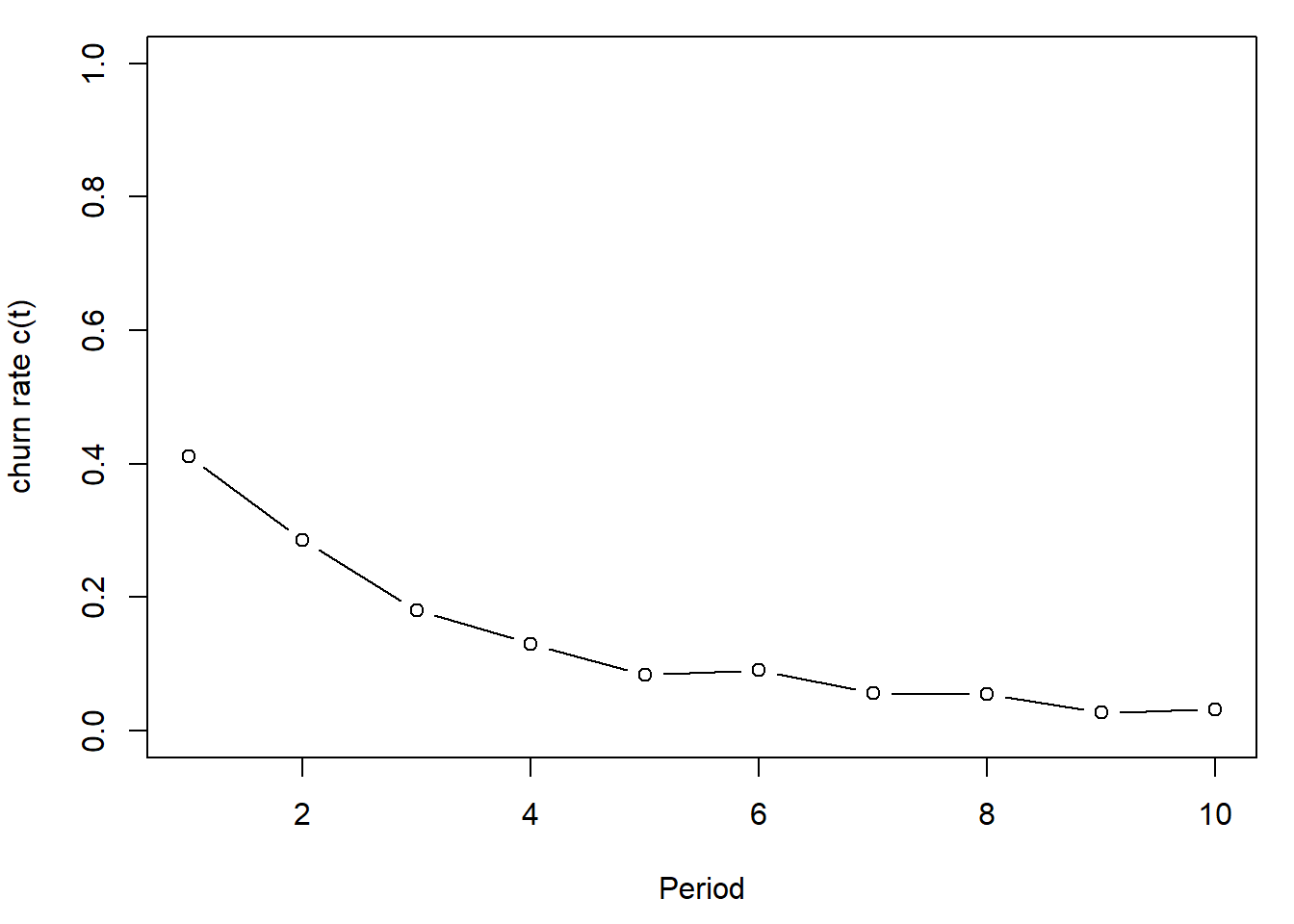
We wrote the retention rate as the fraction of adjacent Survival functions. You can also write the Survival function as the product of retention rates. \[ S(t) = \prod_{j=1}^{t} \; r(j) \]

Geometric model

Assumes a constant retention rate.

Every period you flip a coin and with probability \(p\) you stay.

The probability of lasting more than \(t\) periods is then getting tails \(t\) times in a row. \[ S(t) = p^t \]

There’s one parameter in the model, \(p\). Let’s assume, for example, that \(p = 0.8\).

p <- 0.8    # retention probability (rate) 

t <- seq(0,10)  # time period starting at 0

par(mfrow=c(1,1))
par(mai=c(.8,.8,.2,.2))
plot(t, p^t, type="b",ylab="Probability the customer has survived", xlab="Period", main="Survival function")
text(1.5, .78, " 0.8", cex=1, pos=3, col="black")
text(2.5, .62, parse(text= '.8^2'), cex=1, pos=3, col="black")
text(9.6, .16, parse(text='.8^10'), cex=1, pos=3, col="black")

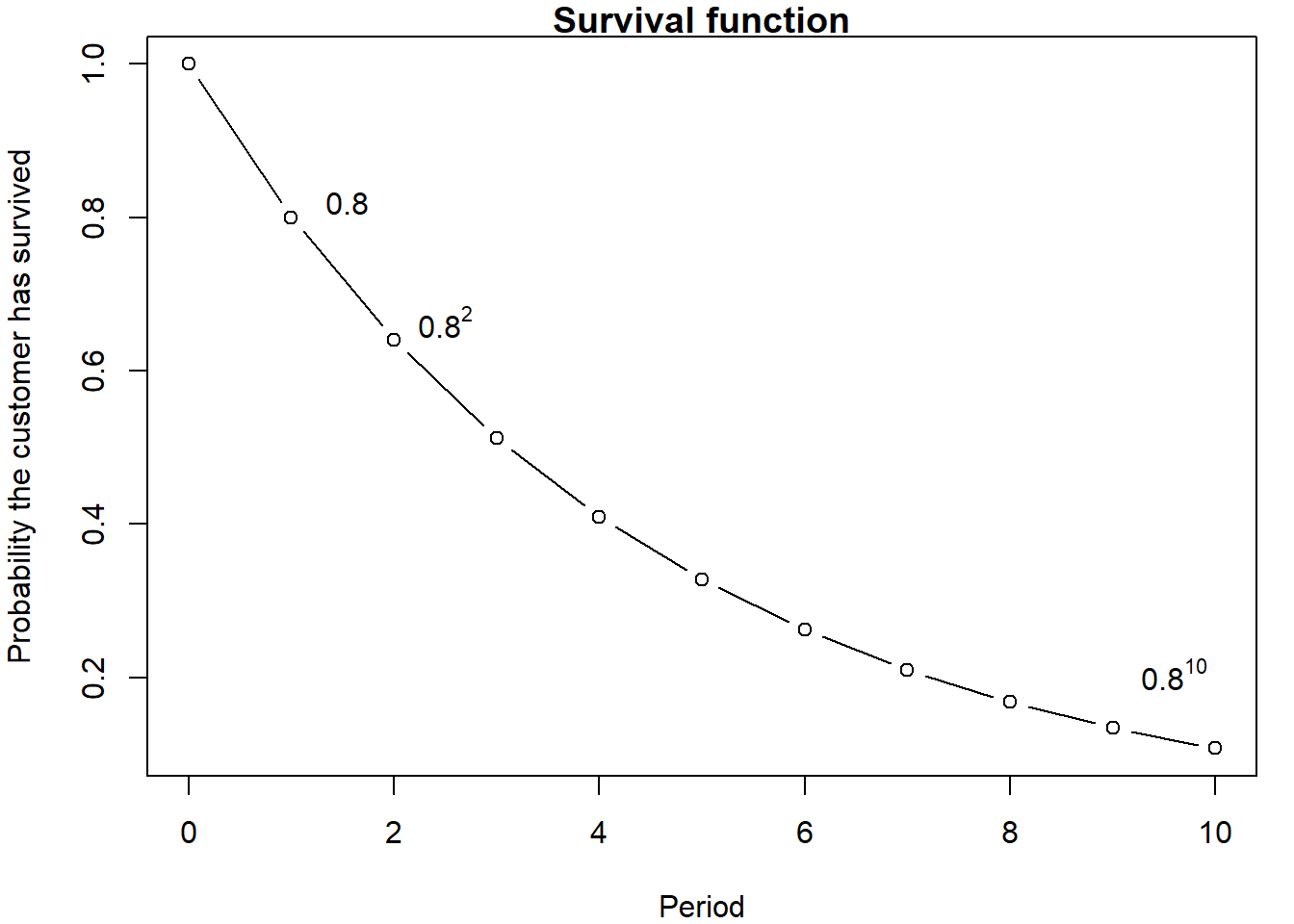
CLV (Homogeneity Case)

CLV is the present value of the expected profits: the margin (assumed constant), multiplied by the probability that the customer survives up until this point.

In the geometric model, \(S(t)=p^t\). We can use the results of a geometric series^[For a geometric series: \[ \begin{array}{ccl} E[CLV] & = & \displaystyle \frac{m \; (1+d)}{1+d-p} \end{array} \] We write a formula to calculate it:

geoCLV <- function(p,m,d){
  m*(1+d)/(1+d-p)
}

p<-0.8    # retention probability (rate) 
m<-100    # margin (profit)
d<-0.1    # discount rate

## Expected Customer Lifetime Value of the new customer
geoCLV(p,m,d)

## [1] 367

We can compare this formula calculated over a infinite horizon to the first 10 terms.

t<-seq(0,10)  # time period starting at 0

m*(p/(1+d))^t # the first 10 terms of CLV

##  [1] 100.00  72.73  52.89  38.47  27.98  20.35  14.80  10.76   7.83   5.69   4.14

sum(m*(p/(1+d))^t)  # CLV using only the first 10 terms

## [1] 356

So the 10-period CLV is 356. It is relatively close to the infinite-horizon CLV, which is 367. Each additional term adds less because the probability of remaining a customer diminishes over time, and discounting diminishes it as well. We will use this fact later on.

Estimating the Geometric Model & Evaluating its Fit

How well does the geometric model describe actual retention behavior?

lost <- -diff(active_cust)
active <- active_cust[-1]

loop.lik <- function(params) {
p <- params[1]
ll <- 0
for (i in 1:length(lost)) {
    ll<-ll+lost[i]*(log(1-p)+(i-1)*log(p))
}
ll <- ll+active[i]*i*log(p)
return(-ll)    #return the negative of the function to maximize likelihood
} 

#find parameters for p with optim
geom <- optimize(loop.lik, c(0, 1), tol = 0.0001)

p_hat <- geom$minimum

Now we can judge the fit of the model by comparing the retention rate and survival function implied by the geometric model to the actual numbers.

par(mfrow=c(1,1))
par(mai=c(.8,.8,.2,.2))
plot(1:10,rep(p_hat,10),ylab="Retention Rate",xlab="Period",main="",ylim=c(.55,1),type="l")
lines(1:10, r, type="b",ylab="retention rate r(t)", xlab="Period",ylim=par("yaxp")[1:2]) 

text(8, .73, "predicted: geom. model", cex=1, pos=3, col="black")
text(6, .95, "actual", cex=1, pos=3, col="black")

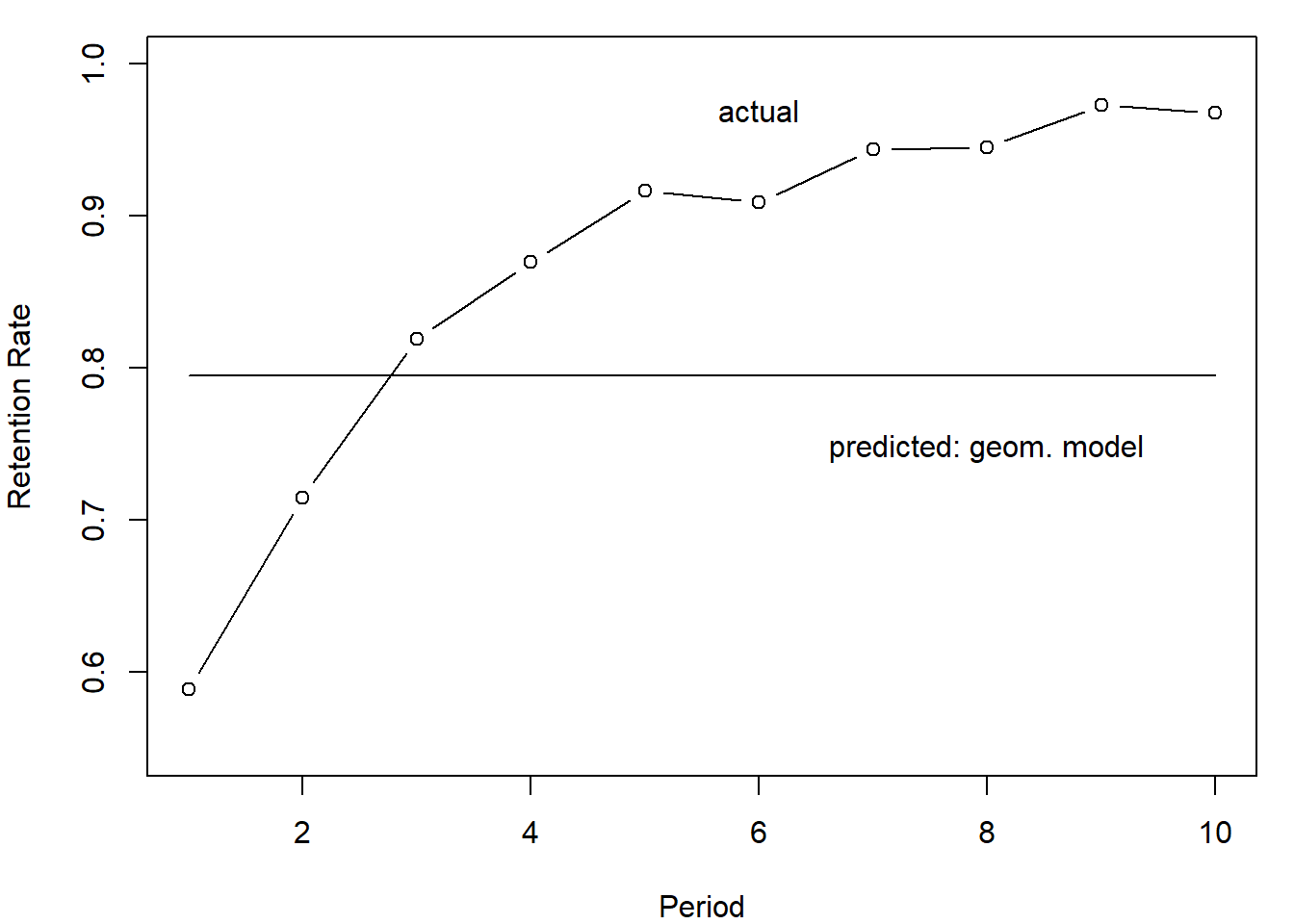
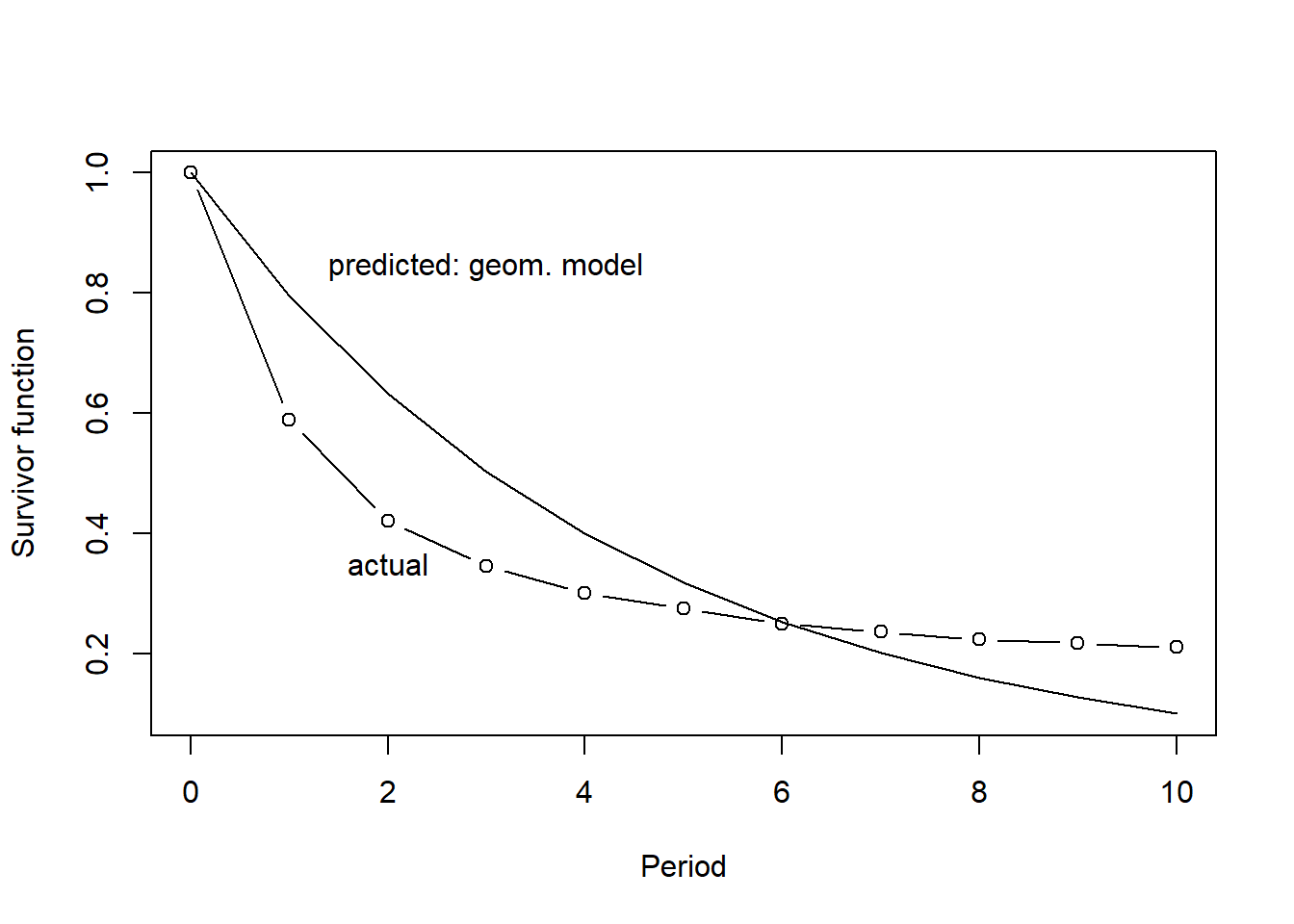
Equivalently for the survival function:

S_geo=p_hat^(0:10)
plot(0:10,S_geo,ylab="Survivor function",xlab="Period",main="",ylim=c(.1,1),type="l")
lines(0:10, S, type="b",ylab="retention rate r(t)", xlab="Period",ylim=par("yaxp")[1:2]) 
text(3, .8, "predicted: geom. model", cex=1, pos=3, col="black")
text(2, .3, "actual", cex=1, pos=3, col="black")

Ruse of heterogeneity

In a given cohort of customers, the retention rate usually increases over time. An “old” customer is more likely to stay than a new one.

Why do retention rates increase over time (for a cohort of customers)?
- This can arise because customers are becoming more loyal. - But it can also be due to heterogeneity in the population with respect to retention rates.

Consider a population of two types of customers: good customers have retention rate of 0.90; bad customers have 0.50. There are twice as many bad as good.

N<-10000
prop<-1/3
n<- data.frame(seg1=rep(NA,10), seg2=rep(NA,10))
ret<-c(.9,.5)
n$seg1[1]<-round(N*prop)
n$seg2[1]<-round((1-prop)*N)

for(k in 2:10){
  n[k,]<-round(n[k-1,]*ret)
}

avgr<-(n$seg1*ret[1]+n$seg2*ret[2])/rowSums(n)
t=seq(1,10)

par(mfrow=c(1,2))
plot(t,avgr,ylab="retention rate",xlab="period",main="",ylim=c(.4,1),type="b", xaxt="none", lwd=3)
axis(1, seq(1,10,1))
abline(h= ret[1], lty=2, lwd=3, col="blue")
abline(h= ret[2], lty=2, lwd=3, col="red")
text(2.5, .78, "avg. ret.")
text(3, .52, "seg. 2", cex=1, pos=3, col="black")
text(3, .92, "seg. 1", cex=1, pos=3, col="black")

plot(t,n$seg2, xlab="period",main="",type="b", lwd=3, xaxt="none", col="red", ylab="Number of customers")
axis(1, seq(1,10,1))
lines(t,n$seg1, lwd=3, type="b", col="blue")
text(4, 3000, "seg. 1", cex=1, pos=3, col="black")
text(2.3, 5000, "seg. 2", cex=1, pos=3, col="black")

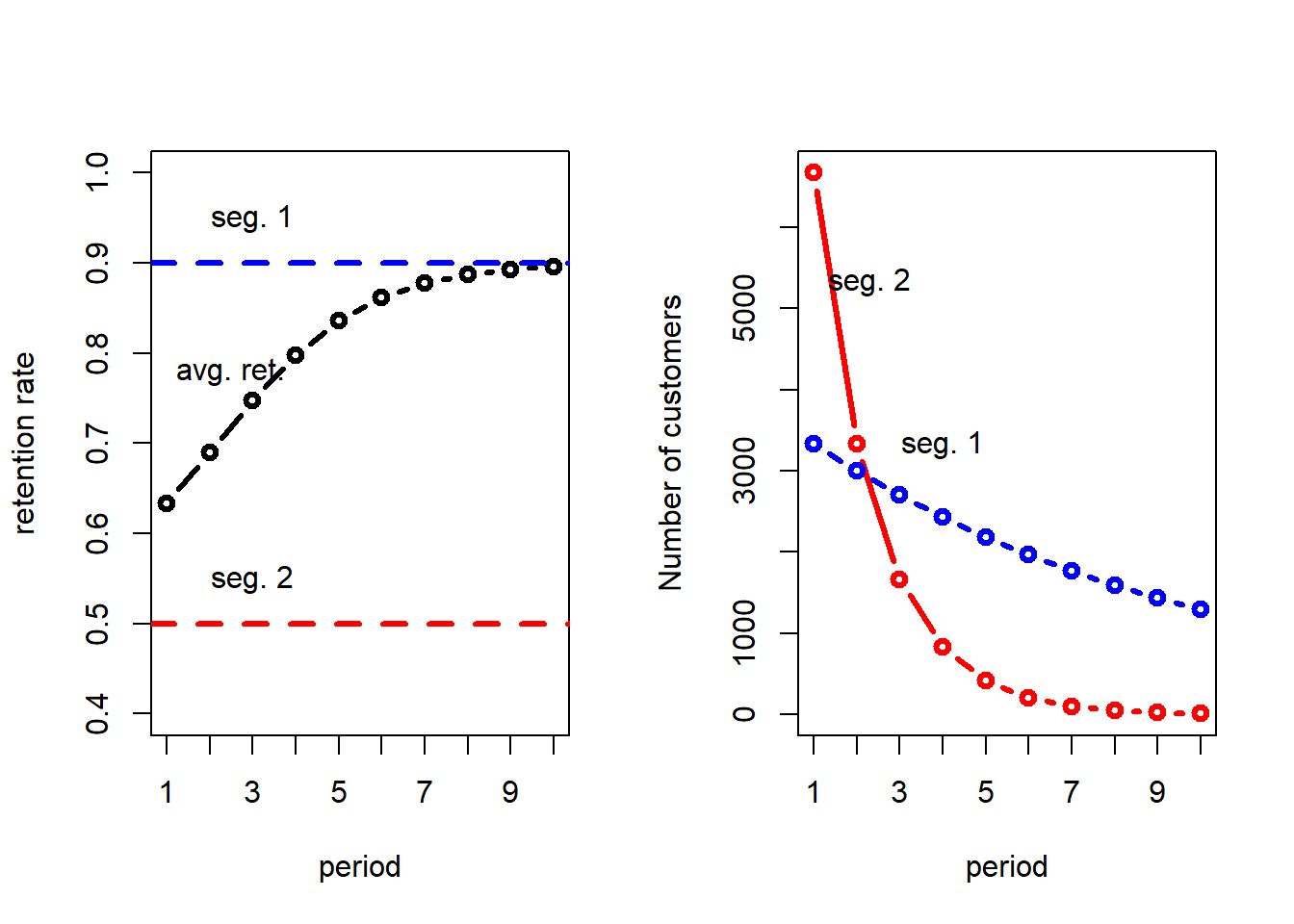
In the beginning, there are more bad than good customers. But by period 3 that changes, as more bad customers quit, leaving more good customers in the cohort.

Shifted Beta geometric

Above we considered two types of customers. Now we build a model where there is a distribution of retention rates across customers.

Conditional on the retention rate, we assume that the probability a customer survives at least \(t\) periods is geometric, as before.

We will rewrite it in terms of the churn rate, \(\theta = 1-p\), rather than the retention rate: \[ S(t \mid \theta) = p^t = (1-\theta)^t \]

We then assume that there is a distribution of churn rates \(\theta\) in the population. This rate has to be between 0 and 1, so we assume it comes from a Beta distribution with parameters \(a\) and \(b\). \(B(a,b)\) is the beta function:

beta(1,5)

## [1] 0.2

The beta distribution is: \[ f(\theta | a,b) = \frac{\theta^{a-1} (1-\theta)^{b-1}}{B(a,b)}, \qquad a>0, b>0\] The retention rate implied by this, using the formula \(r(t)=S(t)/S(t-1)\) is \[ r(t|a,b)=\frac{B(a,b+t)}{B(a,b+t-1)}=\frac{b+t-1}{a+b+t-1} \]

As you can see, this retention rate increases over time. How fast it increases depends on the parameters \(a\) and \(b\).
- If \(a\) and \(b\) are are small, the retention rate increases quickly, but also levels off quickly.
- At medium levels, \(a\) and \(b\) rise at a decreasing rate. - If \(a\) and \(b\) are large, there is hardly any increase. It is essentially equivalent to the geometric model that assumed a constant retetion rate.

t=seq(1,10)
r_sBG=function(a,b,t){
    (b+t-1)/(a+b+t-1)
}
par(mfrow=c(1,1))
plot(t,r_sBG(.1,.3,t),ylab="retention rate",xlab="period",main="retention rate: shifted Beta geometric model for different parameter values",ylim=c(.65,1),type="b", xaxt="none")
points(t,r_sBG(1,3,t),type="b",col="red")
points(t,r_sBG(100,300,t),type="b",col="green")
axis(1, seq(0,10,1))
text(8, .7, "a=100,b=300", cex=1, pos=3, col="black")
text(8, .85, "a=1,b=3", cex=1, pos=3, col="black")
text(8, .94, "a=0.1,b=0.3", cex=1, pos=3, col="black")

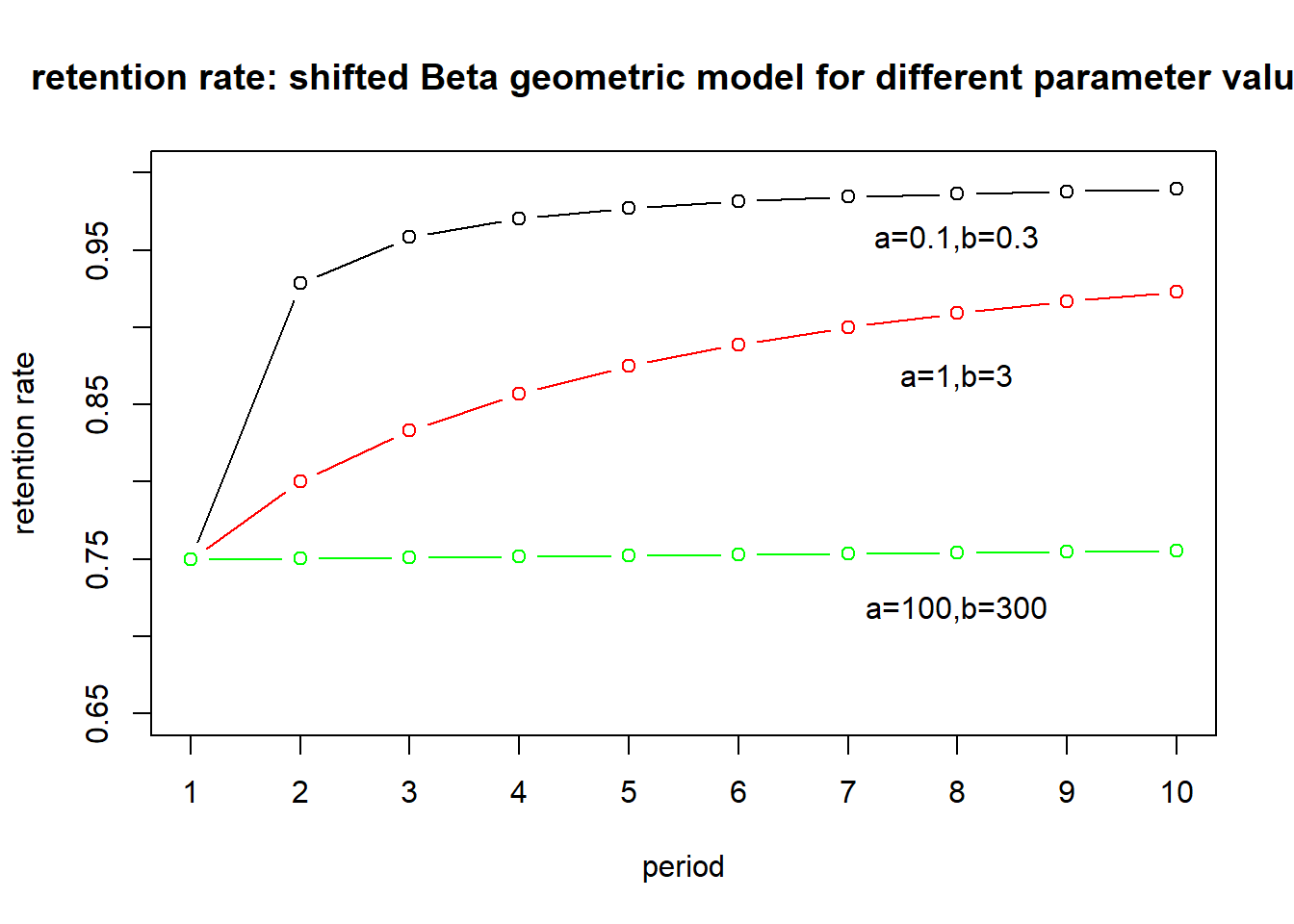
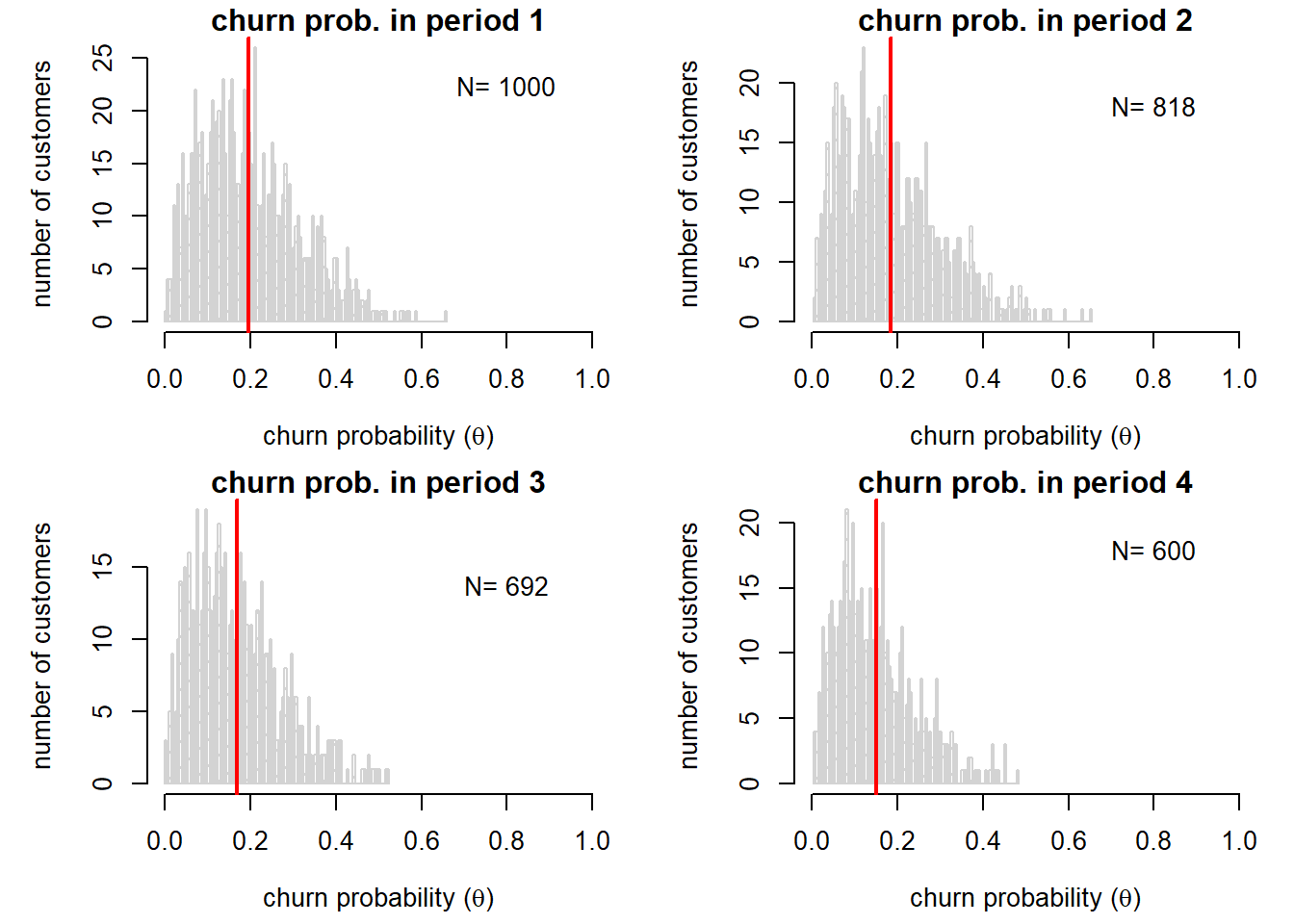
Each period, the high \(\theta\) customers drop out, shrinking the average \(\theta\) across customers. The rate at which this happens depends on the heterogeneity.

set.seed(19103)
N=1000  
a<-2  
b<-8
par(mfrow=c(2,2))
for (t in 1:4){
  cust<-rbeta(N, a,b)  # draw N times from a beta distribution with parameters a and b
  par(mai=c(.7,.8,.2,.2))
  g<-hist(cust,breaks = 99,xlim = c(0,1),density = 10, main=paste("churn prob. in period", t), xlab =     expression(paste("churn probability (", theta, ")")), ylab = "number of customers",)
    text(.8,.8*par("yaxp")[2], paste("N=",round(N)),cex=1,pos=3,col="black")
    abline(v=mean(cust),col = "red", lwd = 2) # draw average churn
  b<-b+1  # Bayes update churn distribution
  N<-N*(b+t-1)/(a+b+t-1) # churners leave
}

Estimating the model

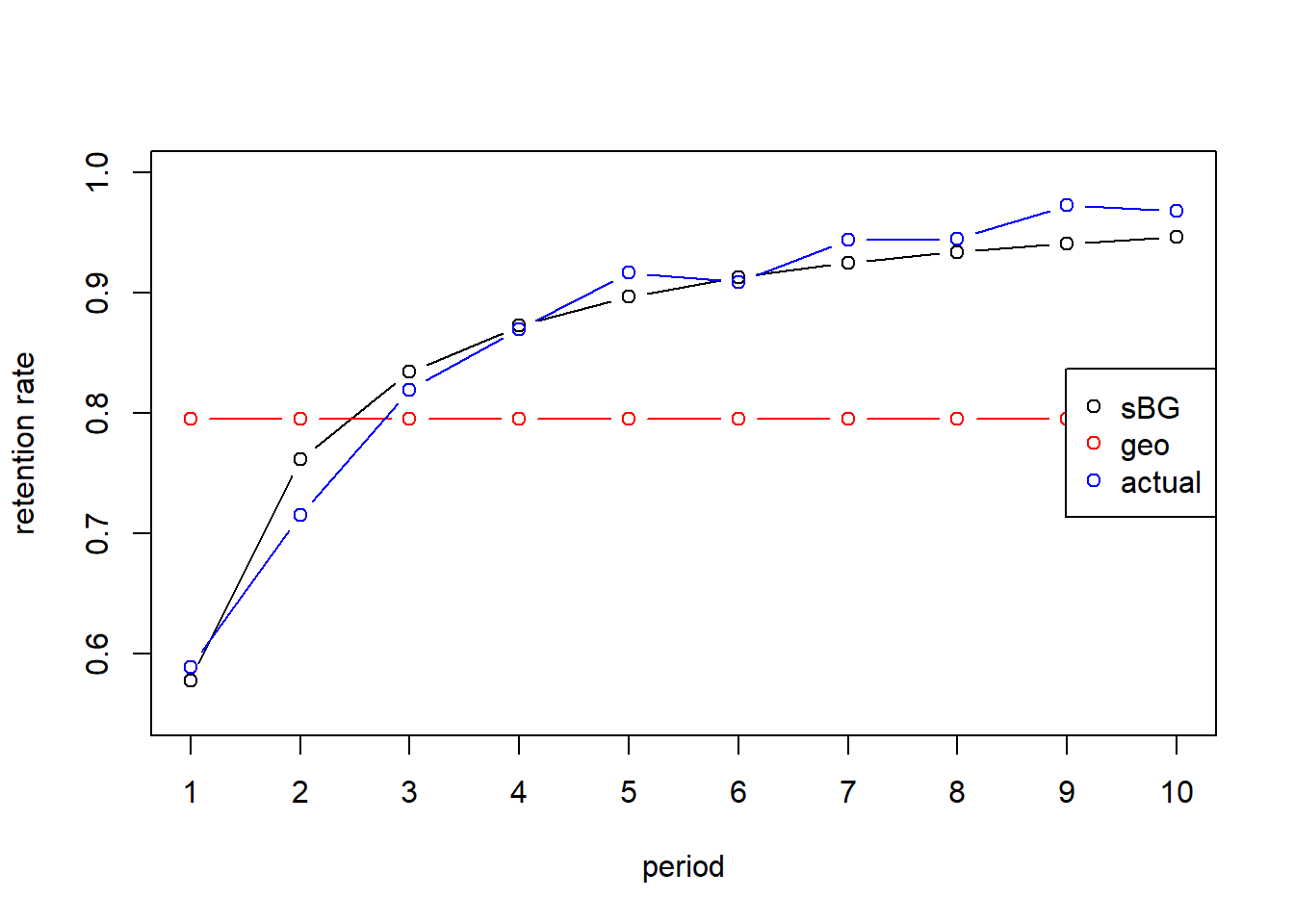
You can estimate the model using maximum likelihood.

We get parameters \(a\) and \(b\). Then we can forecast \(r(t)\) and compare the predicted retention to the actual retention rate.

loop.lik<-function(params) {
a<-params[1]
b<-params[2]
ll<-0
for (i in 1:length(lost)) {
    ll<-ll+lost[i]*log(beta(a+1,b+i-1)/beta(a,b))
}
ll<-ll+active[i]*log(beta(a,b+i)/beta(a,b))
return(-ll)    #return the negative of the function to maximize likelihood
} 

#find parameters for a and b with optim
sBG<-optim(par=c(1,1),loop.lik)

a<-sBG$par[1]
b<-sBG$par[2]

#calculate retention using model parameters
t<-1:length(active)
r_pred<-r_sBG(a,b,t)

# plot actual and predicted retention rate
#rep(p_hat,10)
#t
par(mfrow=c(1,1))
plot(t,r_pred,ylab="retention rate",xlab="period",type="b", xaxt="none", ylim = c(.55,1))
lines(t,rep(p_hat,10),type="b",col="red")
lines(t,r, type="b", col="blue")
axis(1, seq(0,10,1))
legend('right',legend=c("sBG", "geo", "actual"),col=c("black","red","blue"), pch=c(1,1))

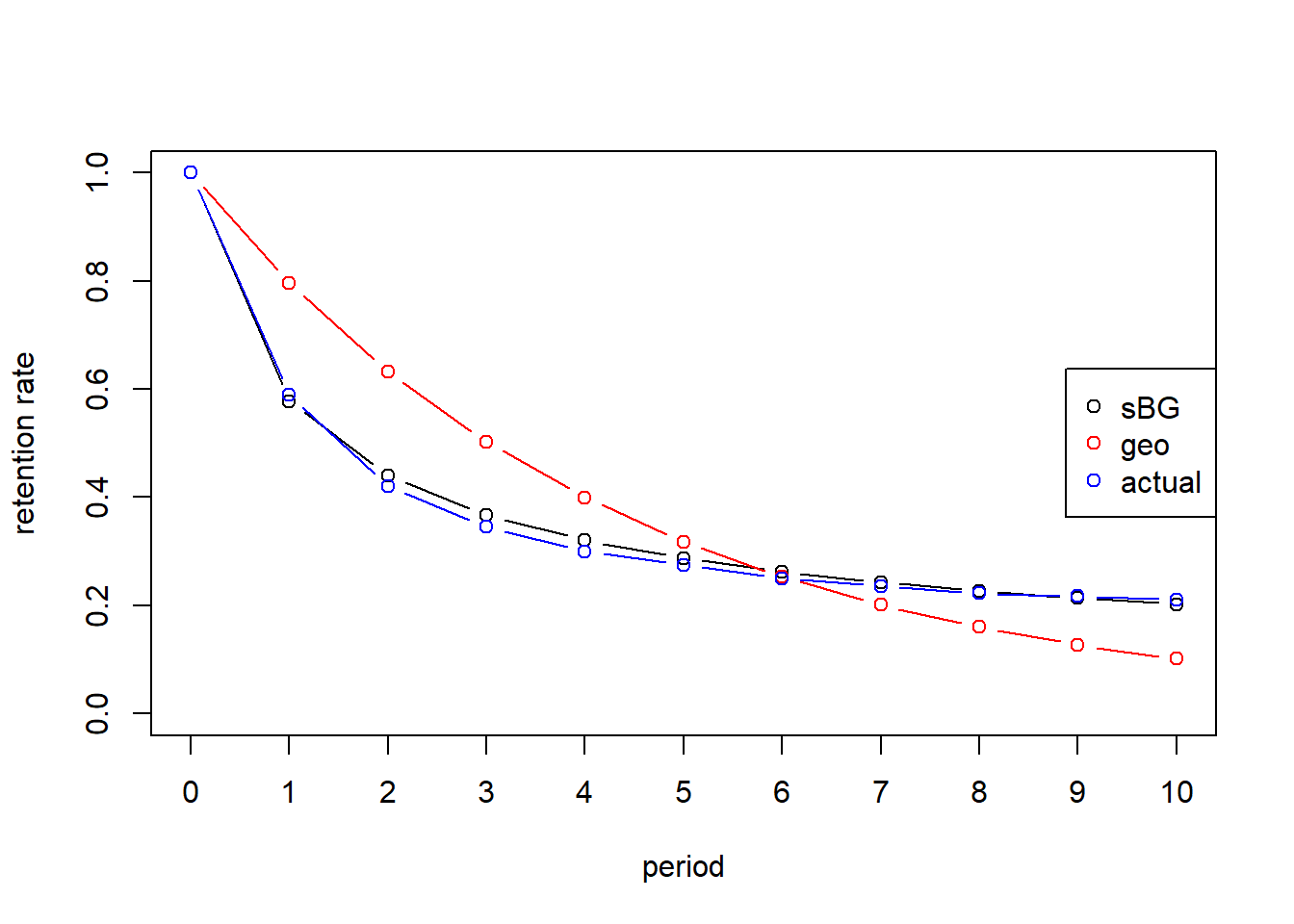
S_pred<-c(1,cumprod(r_pred)) # predicted survivor function
S_geo<-p_hat^(c(0,t))

t<-seq(0,10)
par(mfrow=c(1,1))
plot(t,S_pred,ylab="retention rate",xlab="period",type="b", xaxt="none", ylim = c(0,1))
lines(t,S_geo,type="b",col="red")
lines(t,S, type="b", col="blue")
axis(1, seq(0,10,1))
legend('right',legend=c("sBG", "geo", "actual"),col=c("black","red","blue"), pch=c(1,1))

Calculating CLV with the sBG

In the geometric model, we could use the properties of a geometric series to derive CLV over an infinite time horizon. With the sBG, we have no such closed form expression. Instead, we can set the time horizon \(T\) at some large number, like \(200\), and sum up the first \(T\) terms of the CLV expression. Because of discounting and the diminishing survival function, each additional term contributes less to CLV. So after a suitably large \(T\), we can safely ignore the later terms.

\[ E[CLV] = m + \frac{m \; S(1)}{(1+d)^1} + \frac{m \; S(2)}{(1+d)^2} + \frac{m \; S(3)}{(1+d)^3} + \cdots + \frac{m \; S(T)}{(1+d)^T} \]

Since we have parameters \(a\) and \(b\), we can project \(r(t)\) and therefore \(S(t)\). The code below does this.

t<-seq(1,200) # time periods
r_pred <- r_sBG(a,b,t) # predicted retention rate
S_pred <- c(1,cumprod(r_pred)[1:199]) # predicted survivor function

dis <- 1/(1+d)^(t-1) # discount factor, first term is present so no discounting

CLV_sBG<-sum(m*S_pred*dis) # the sum of margin x survivor x discount factor

CLV_sBG

## [1] 368

# compare with the geometric CLV model
geo<-geoCLV(p_hat,m,d) 
geo

## [1] 361

The CLV we calculate using the sBG model is 368, slightly higher than what we would predict with the geometric model, 361.

While it doesn’t seem like much, the big difference will come when we calculate RLV. Why? Because the geometric model says there is no difference between old and new customers. The sBG model says there is a difference, due to heterogeneity and sorting.

RLV with the sBG

We know from above that the sBG model leads to customers with higher churn probabilities dropping out earlier, the sorting mechanism we described earlier. Hence a customer who has remained for so many periods will likely have a lower churn probability than a new customer. In the geometric model, this makes no difference: everyone has the same \(\theta\). But in the sBG model, it does make a difference due to heterogeneity.

CLV refers to new customers, but what about those who we have observed for some time? Residual lifetime value (RLV) is the term for already acquired customers, as opposed to new customers.

The conditional probability of a customer who has survived \(\tau\) periods surviving \(s>\tau\) periods is: \[ P(T>s | T > \tau) = \frac{S(s)}{S(\tau)} \quad \textrm{where} \; s > \tau \]

For RLV, we calculate right before the renewal decision.

Let’s try this out for someone who has renewed \(\tau = 4\) times. We are standing just before period 5: does this person, who has survived 4 periods, survive once more? The probability that he/she does is \(\frac{S(5)}{S(4)}\).

tau <- 4

t <- seq(1,tau+200)
r_pred <- r_sBG(a,b,t)
S_pred <- cumprod(r_pred)

S_shift <- S_pred[(tau+1):length(S_pred)]  # survival function from tau + 1 until T

dis<-1/(1+d)^(t(1:200)-1) # discount rate

RLV_sBG<-sum(m*S_shift/S_pred[tau]*dis)  # sum of margin x S(tau + t)/ S(tau) x discount

RLV_sBG

## [1] 650

We calculate the RLV as 650, which is substantially higher CLV 368, because RLV is for already existing customers who are likely to have lower churn probabilities than new customers. The implication is that heterogeneity and sorting are important. As time passes, the customer base shrinks and those who remain are increasingly likely to stay longer.

The RLV formula for geometric model right before renewing is: \[ E[RLV]= m p + \frac{m \; p^2}{(1+d)} + \frac{m \; p^3}{(1+d)^2} + \dots = \frac{mp(1+d)}{1+d-p} \] Plugging some numbers in, we see that the RLV is substantially lower in the geometric model.

RLV_geo<-m*p_hat*(1+d)/(1+d-p_hat)
RLV_geo

## [1] 287

The RLV using the geometric model is 287, substantially less than that of the sBG model.