Tutorial 3: Logit Regressions

Introduction

Logistic regression is the most commonly used statistical technique for binary response data. Many marketing applications are concerning binary consumer decisions:

• does a consumer respond or not respond to marketing?
• do they subscribe or not subscribe?
• do they churn or not churn?

We’ll use a data set on customer churn for a telecommunications company with several different services. We’ll use demographic, service usage, and customer history to predict churn. We then apply this model to a new, holdout set of customers. We calclate the confusion matrix, the lift table, and use it to do targeted proactive churn selection.

Installing the packages and loading the data

# install.packages("pRoc")
# install.packages("plotrix")   
library(car)
library(tidyverse)
library(pROC)
library(plotrix)  
library(tidyverse)
library(readr)
library(kableExtra)

# set working directory 
telco <- read_csv("telco.csv")
telco_holdout <- read_csv("telco_holdout.csv")

options("scipen"=200, "digits"=3)

Inspecting the data

Let’s get rid of the ID column, since we never need to use it. We’ll make senior citizen a factor variable, and recode total charges so that it’s in thousands of dollars. We also need to recode Churn for yes/no to 0/1.

# drop the ID column, make senior citizen a factor variable, and divide totalcharges by 1000
telco <- telco[-c(1)]
telco$SeniorCitizen<-as.factor(telco$SeniorCitizen)
telco$TotalCharges<-telco$TotalCharges/1000

# Change Churn from "no" "yes" to 0 1
telco <- telco %>%
      mutate(Churn = ifelse(Churn == "No",0,1))

Churn

What fraction of customers churn (quit)? This is the dependent variable we want to predict. We need to use the “as.numeric” function to transform it from a factor variable to a 0/1 continuous variable in R. We report the average churn rate of the customer below.

summary(telco$Churn)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   0.000   0.000   0.000   0.266   1.000   1.000

rbar <- mean(telco$Churn)

The average churn rate in the customer base is 0.266.

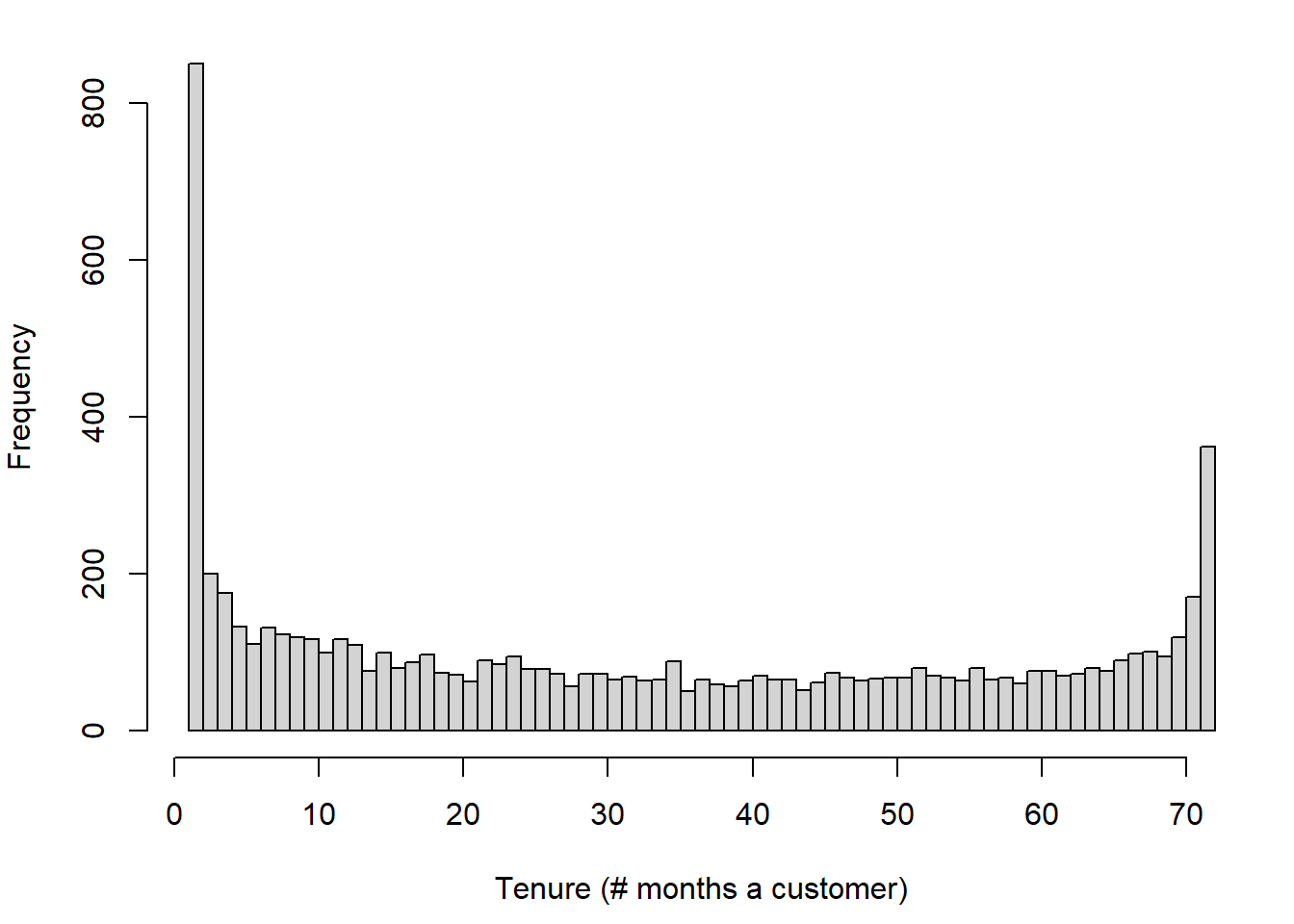
Tenure

One important driver of churn is likely to be tenure, how long a customer has been a customer for. We can see below that there is a spike at 1, many customers just started, and a smaller peak at 72.

par(mai=c(.9,.8,.2,.2))
hist(telco$tenure, main = "", xlab="Tenure (# months a customer)", breaks = 71)

Churn Rate Variation

How does the rate churn vary by tenure? We create a dataset of length 72, one for each level of tenure. We calculate the proportion churning, number of churners (n_churn), number of customers in the tenure group, the standard error of the proportion churning (discussed in previous lectures), and the lower and upper confidence intervals.

churn_tenure <- telco %>% 
  as.data.frame() %>% 
  group_by(tenure) %>% 
  summarize(tenure=mean(tenure), 
            p_churn=mean(Churn), 
            n_churners=sum(Churn), n=n(), 
            p_churn_se= sqrt((p_churn)*(1-p_churn)/n)) %>% 
  mutate(lower_CI_pchurn = p_churn - 1.96*p_churn_se, ## CI of churn by tenure-lev.
         upper_CI_pchurn = p_churn + 1.96*p_churn_se) 
head(churn_tenure) %>% 
  kbl() %>%
  kable_styling()

tenure	p_churn	n_churners	n	p_churn_se	lower_CI_pchurn	upper_CI_pchurn
1	0.620	380	613	0.020	0.581	0.658
2	0.517	123	238	0.032	0.453	0.580
3	0.470	94	200	0.035	0.401	0.539
4	0.472	83	176	0.038	0.398	0.545
5	0.481	64	133	0.043	0.396	0.566
6	0.364	40	110	0.046	0.274	0.454

par(mai=c(.9,.8,.2,.2))
plot(x = churn_tenure$tenure, y = churn_tenure$p_churn, main="Proportion of customers who churn by tenure", xlab="Tenure (# months a customer)", ylab="proportion of customer churning")

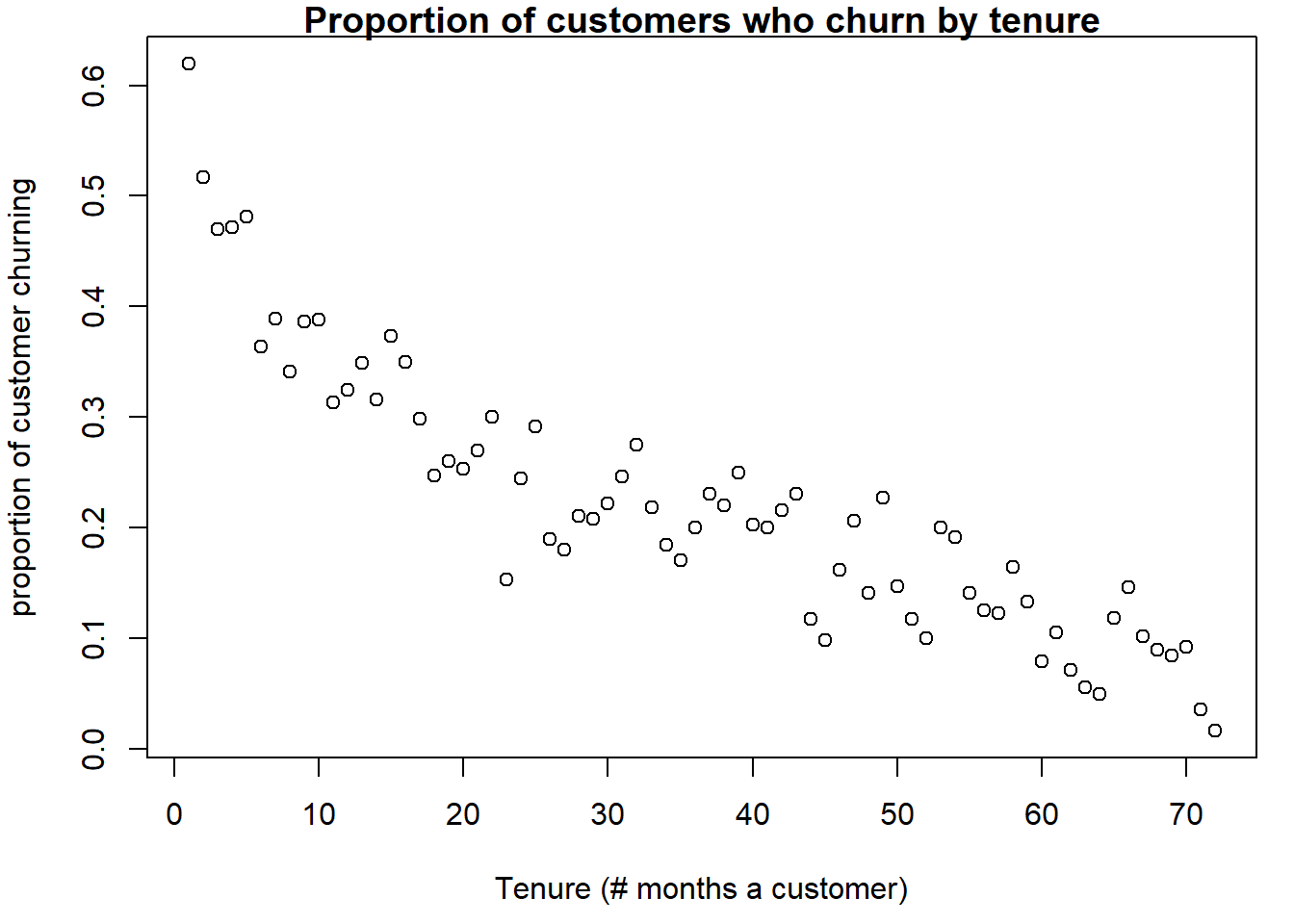
The figure shows a clear negative relationship: the longer the customer has been a customer, the lower the probability of churn (churn rate).

Estimating the logistic regression

• Model 0 is the simplest: The only variable is tenure and it is treated as a continuous variable.

# fit 
model_0 <- glm(Churn ~ tenure, data=telco, family = binomial(link="logit"))

# show us coefficients and other model fit statistics
summary(model_0)

## 
## Call:
## glm(formula = Churn ~ tenure, family = binomial(link = "logit"), 
##     data = telco)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -1.177  -0.840  -0.479   1.178   2.380  
## 
## Coefficients:
##             Estimate Std. Error z value            Pr(>|z|)    
## (Intercept)  0.03730    0.04232    0.88                0.38    
## tenure      -0.03901    0.00141  -27.69 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 8143.4  on 7031  degrees of freedom
## Residual deviance: 7176.3  on 7030  degrees of freedom
## AIC: 7180
## 
## Number of Fisher Scoring iterations: 4

## [1] -0.0383

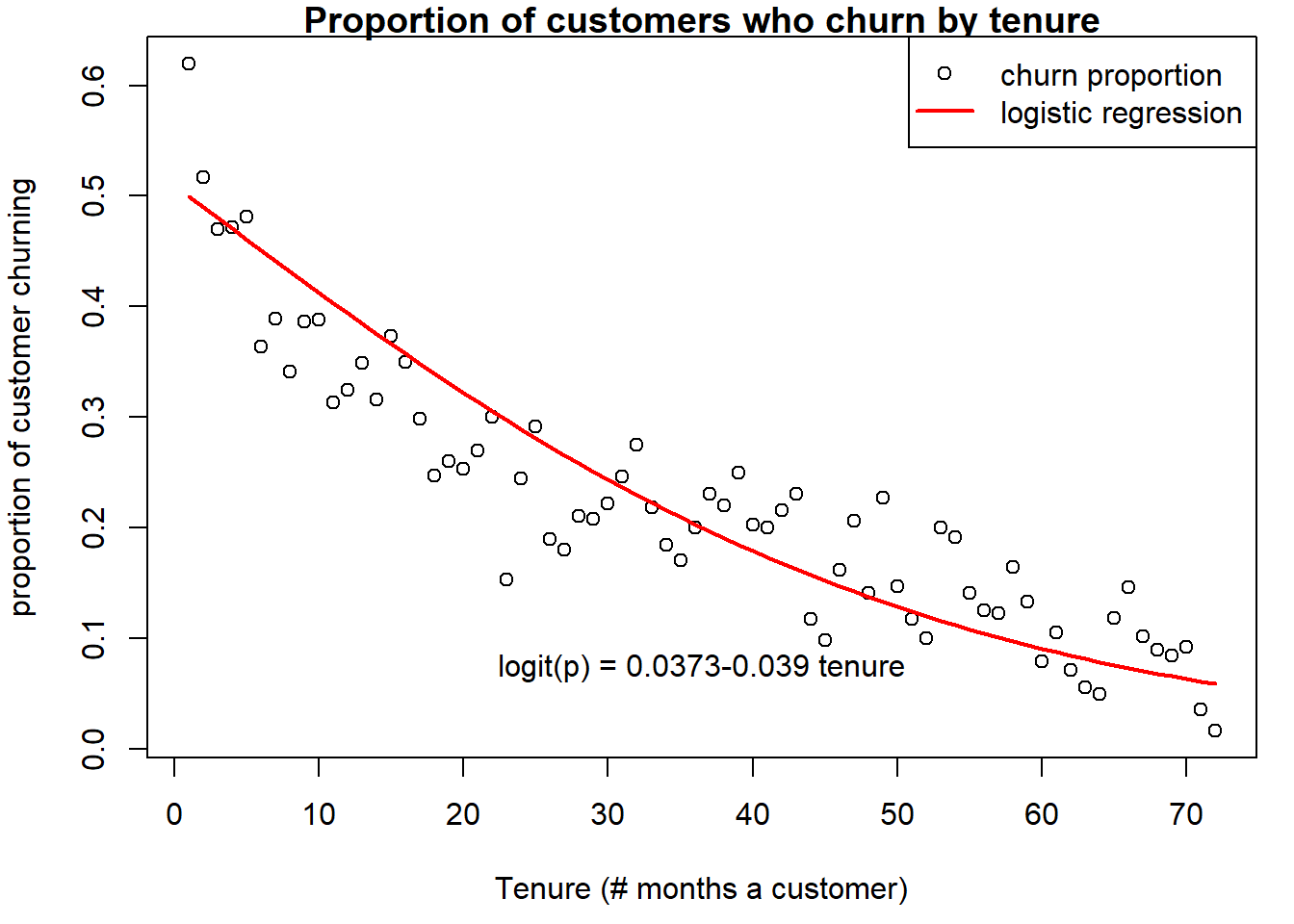
Interpretation: Having 1 additional unit of tenure of decreases the odds of churn by 0.0383or by 3.8%.

Plot: Compare observed proportion of churn by tenure calculated separately for each level of tenure; with model predictions.

I’m just creating a new data with the regression results:

# create data set of tenure from 1 to 72
plotdat <- data.frame(tenure=(1:72))

# put predictions and 95% confidence intervals of those 
preddat <- predict(model_0,
               type = "link",
               newdata=plotdat, ## Prediction by each level of tenure
               se.fit=TRUE) %>% 
  as.data.frame() %>% 
  mutate(tenure=(1:72), ### HERE we are putting our results ####
 # model object model_0 has a component called linkinv that 
 # is a function that inverts the link function of the GLM:
         lower = model_0$family$linkinv(fit - 1.96*se.fit), 
         point.estimate = model_0$family$linkinv(fit), 
         upper = model_0$family$linkinv(fit + 1.96*se.fit))

Final Plot:

# plot actual vs. logistic regression
par(mai=c(.9,.8,.2,.2))
plot(x = churn_tenure$tenure, y = churn_tenure$p_churn, main="Proportion of customers who churn by tenure", xlab="Tenure (# months a customer)", ylab="proportion of customer churning")
lines(x=preddat$tenure, y=preddat$point.estimate, col="red", lwd=2)
legend('topright',legend=c("churn proportion", "logistic regression"),col=c("black","red"),pch=c(1,NA),lty=c(NA,1), lwd=c(NA,2))

eq <- paste0("logit(p) = ",round(coef(model_0)[1],4),
             ifelse(coef(model_0)[2]<0,round(coef(model_0)[2],4),
                    paste("+",round(coef(model_0)[2],4))),
                    paste(" tenure"))
# puts equation in figure
mtext(eq, 1,-3)

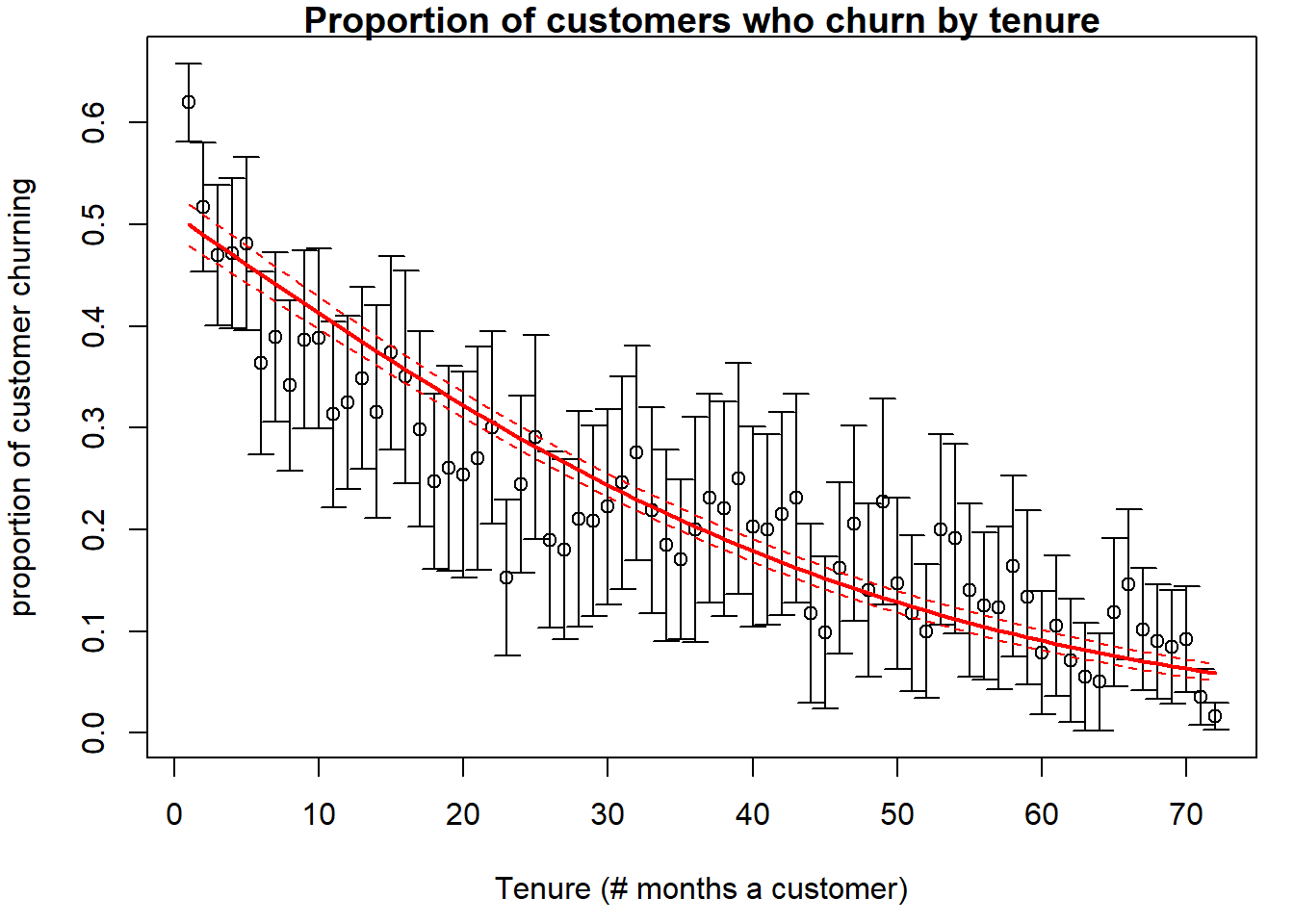
Compare the confidence intervals of the model predictions (dashed red) to those by doing them separately for each level of tenure. You can see we get quite a reduction in uncertainty by having a model that relates these proportions to each other.

The cost of our lower error or error reduction is higher bias – if the model’s functional form deviates from the actual response rate. In other words, we have reduced variance, but at the expense of bias.

par(mai=c(.9,.8,.2,.2))
plotCI(x = churn_tenure$tenure,               # plotrix plot with confidence intervals
       y = churn_tenure$p_churn,
       li = churn_tenure$lower_CI_pchurn,
       ui = churn_tenure$upper_CI_pchurn, main="Proportion of customers who churn by tenure", xlab="Tenure (# months a customer)", ylab="proportion of customer churning")

lines(x=preddat$tenure, y=preddat$point.estimate, col="red", lwd=2, type = "l")
lines(x=preddat$tenure, y=preddat$lower, col="red", lty=2, lwd=1, type = "l")
lines(x=preddat$tenure, y=preddat$upper, col="red", lty=2, lwd=1, type = "l")

• Model 1 is more complex: every variable is included, not just tenure; tenure is treated as a continuous variable as before.

options(width = 200)
model_1 <- glm(Churn ~ . , data=telco, family="binomial")

• Model 2 is more complex: like Model 1, except that tenure is treated a categorical variable. In other words there is a dummy variable for every level of tenure but one. This way, we can flexibly capture a pattern between tenure and churn. In R, all you have to do is write as.factor(tenure) instead of tenure.

model_2 <- glm(Churn ~ . +as.factor(tenure) -tenure , data=telco, family="binomial")

• Model 2 has 94 coefficients.
• Model 3 is the most complex: like Model 2, except that there is an interaction between payment type and tenure. Note in general and interaction is the coefficient on the product of two variables.

model_3 <- glm(Churn ~ . +as.factor(tenure)*as.factor(PaymentMethod) -tenure -PaymentMethod, data=telco, family="binomial")

• Model 3 has 307 coefficients. Note a lot of them have large coefficients and large standard errors. If a variable is zero almost always, (tenure==34)*(PaymentMethod==Electronic check), there is little variation to estimate the coefficient, making it look unstable.

• So, we’ve estimated 3 models each one increasing in the number of coefficients. Let’s see how well they predict.

Deviance and proportion of deviance explained (R2)

Deviance is an error measure, \(-2 \ln(\textrm{likelihood})\). We want it to be as small as possible. The difference between the residual and the null deviance then gives us some sense of how well our model fits overall, taken together.

You can also look at the proportion of deviance explained by the variables in the model.

\[ R^2 = \frac{D_0 - D}{D_0} = 1 - \frac{D}{D_0} \]

models <- paste0("model_", 0:3) # list of models
D <- sapply(models, function(x) get(x)$deviance) # get deviance D for each
D0 <- model_0$null.deviance # D_0 is the same for all models
R2 <- 1-D/D0

par(mai=c(.9,.8,.2,.2))
barplot(R2, names.arg = c("model 0","model 1", "model 2", "model 3"), main=expression(paste("In-Sample R"^"2")), xlab="Model", ylab=expression(paste("R"^"2")))

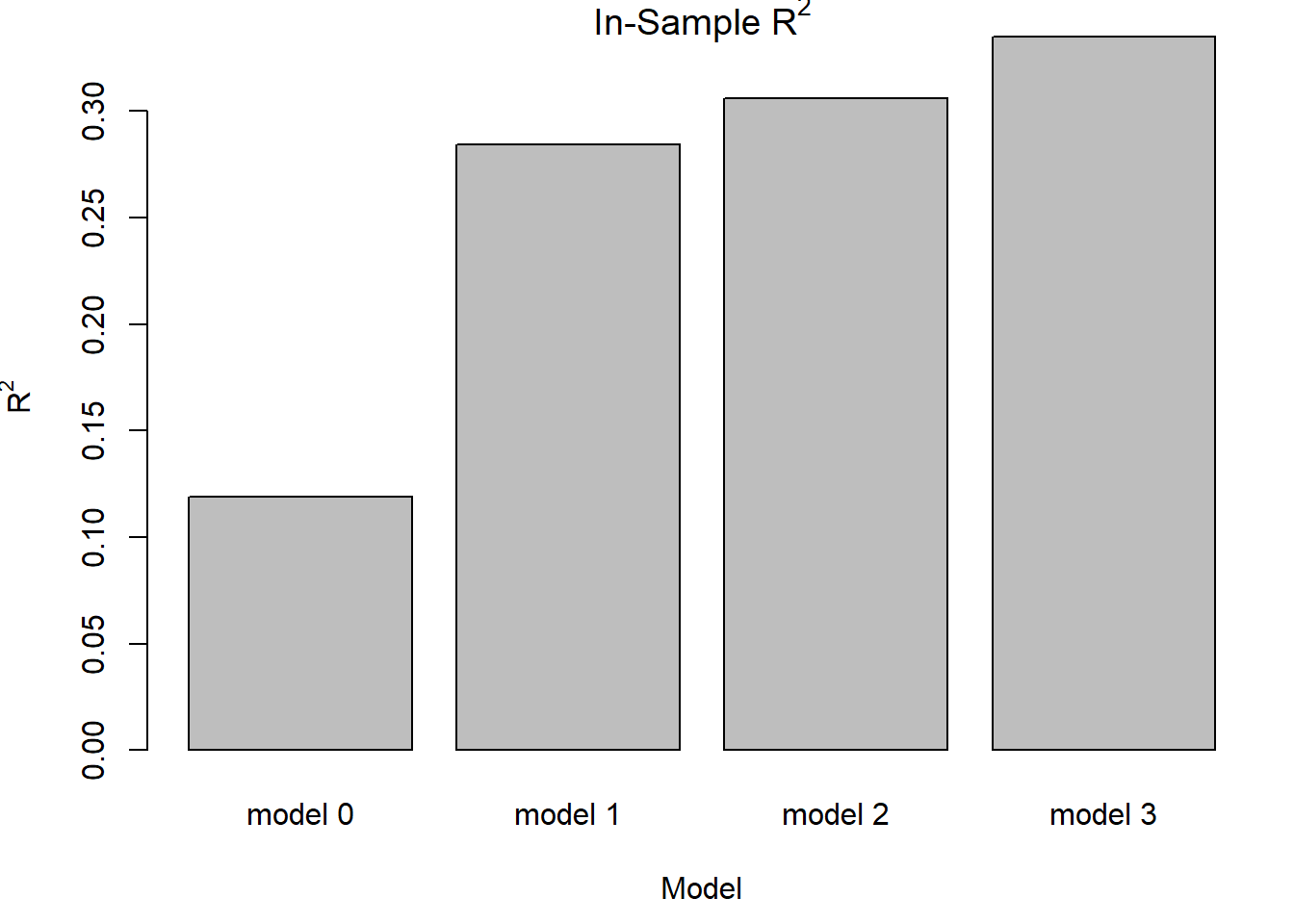
Models 0, 1, 2 and 3 are explaining 12% 28%, 31% and 34%, respectively, of the deviance in customer churn.

Overfitting, K-fold out of sample

But, is the better performance of model a result of overfitting?

What we really care about is being able to predict new data. The R2 and deviance measures are all about in-sample, not out-of-sample fit. So it doesn’t tell us how well our model performs on other data.

We can mimic the presence of new data by holding out part of the data.

We use K-fold out of sample validation.

# you don't need to know how to write this code.
set.seed(19103)
n = nrow(telco)
K = 10 # # folds
foldid = rep(1:K, each=ceiling(n/K))[sample(1:n)]
# foldid[1:10]
OOS <- data.frame(model0=rep(NA, K), model1=rep(NA,K), model2=rep(NA,K), model3=rep(NA,K))


## pred must be probabilities (0<pred<1) for binomial
  deviance <- function(y, pred, family=c("gaussian","binomial")){
    family <- match.arg(family)
    if(family=="gaussian"){
      return( sum( (y-pred)^2 ) )
    }else{
      if(is.factor(y)) y <- as.numeric(y)>1
      return( -2*sum( y*log(pred) + (1-y)*log(1-pred) ) )
    }
  }

## get null devaince too, and return R2
  R2 <- function(y, pred, family=c("gaussian","binomial")){
  fam <- match.arg(family)
  if(fam=="binomial"){
    if(is.factor(y)){ y <- as.numeric(y)>1 }
  }
  dev <- deviance(y, pred, family=fam)
  dev0 <- deviance(y, mean(y), family=fam)
  return(1-dev/dev0)
  }  

# this part will take several minutes, fitting 3 models K times each
  
for(k in 1:K){
  train = which(foldid!=k) # data used to train
  
  # fit regressions
  model_0<- glm(Churn ~ tenure, data=telco[train,], family="binomial")
  summary(model_0)
  
  model_1 <- glm(Churn ~ . , data=telco[train,], family="binomial")
  summary(model_1)
  
  model_2 <- glm(Churn ~ . +as.factor(tenure) -tenure, data=telco[train,], family="binomial")
  summary(model_2)
  
  model_3 <- glm(Churn ~ . +as.factor(tenure)*as.factor(PaymentMethod) -tenure -PaymentMethod, data=telco[train,], family="binomial")
  summary(model_3)
  
  
  # predict on holdout data (-train)
  pred0<- predict(model_0, newdata=telco[-train,], type = "response")
  pred1<- predict(model_1, newdata=telco[-train,], type = "response")
  pred2<- predict(model_2, newdata=telco[-train,], type = "response")
  pred3<- predict(model_3, newdata=telco[-train,], type = "response")
  
  # calculate R2
  OOS$model0[k]<-R2(y = telco$Churn[-train],pred=pred0, family="binomial")
  OOS$model1[k]<-R2(y = telco$Churn[-train],pred=pred1, family="binomial")
  OOS$model2[k]<-R2(y = telco$Churn[-train],pred=pred2, family="binomial")
  OOS$model3[k]<-R2(y = telco$Churn[-train],pred=pred3, family="binomial")
  
  # print progress
  cat(k, "  ")
    
}

## 1   2   3   4   5   6   7   8   9   10

Plot Results:

par(mai=c(.9,.8,.2,.2))  
boxplot(OOS[,1:4], data=OOS, main=expression(paste("Out-of-Sample R"^"2")),
        xlab="Model", ylab=expression(paste("R"^"2")))

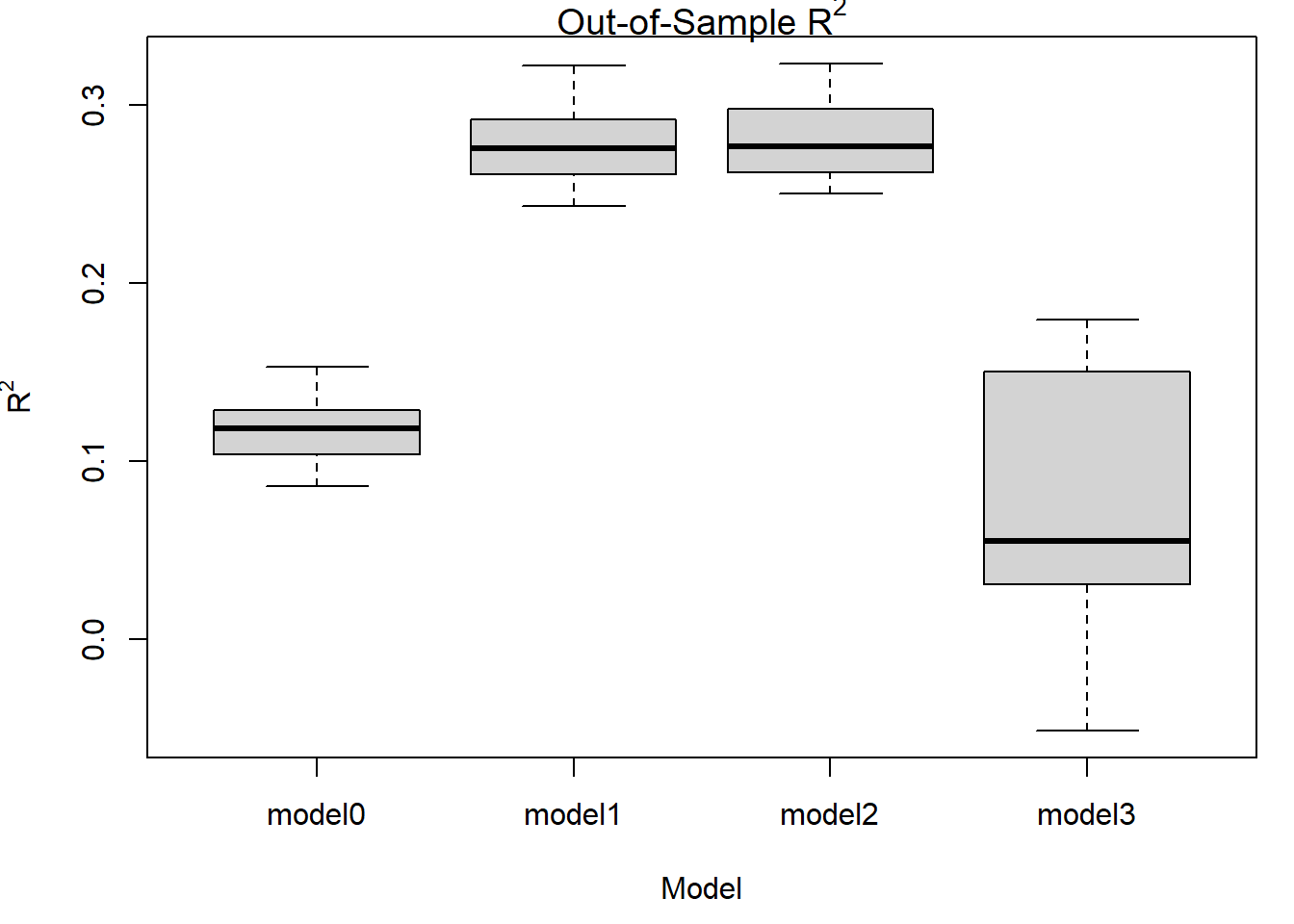
• Model 3 had the highest in-sample \(R^2\), and now it has the worst out-of-sample \(R^2\). It’s even negative!

• Bottom line: Model 3 is over-fitting. It is capturing patterns in the in-sample data that do not generalize to the out-of-sample data. This is why it does such a poor job at predicting.

• Models 1 and 2 have basically the same out of sample \(R^2\).

• This means favoring the simpler models. Model 1, being the simplest, and tied for the best predictive performance is the winner.

Predict

Here we use model 1 to predict the probability of default for a certain customer with a specific profile: a male, senior citizen without a partner or dependents, etc. See below.

newdata = data.frame(gender = "Male", SeniorCitizen=as.factor(1),Partner="No",Dependents="No", tenure=72,PhoneService="Yes",MultipleLines="No", InternetService="DSL", OnlineSecurity="No", OnlineBackup="No", DeviceProtection="No", TechSupport="Yes", StreamingTV="Yes", StreamingMovies="No", Contract="One year", PaperlessBilling="No", PaymentMethod="Mailed check", MonthlyCharges=30,TotalCharges=1)

predict(model_1,newdata,type="response")

##      1 
## 0.0166

The probability of churn is low.

Holdout sample

Now we look at how well model 1 performs on one holdout sample, holdout_telco.csv.

The churn rate we see in the holdout sample, 0.274, is close to that in the estimation sample we used earlier, 0.266.

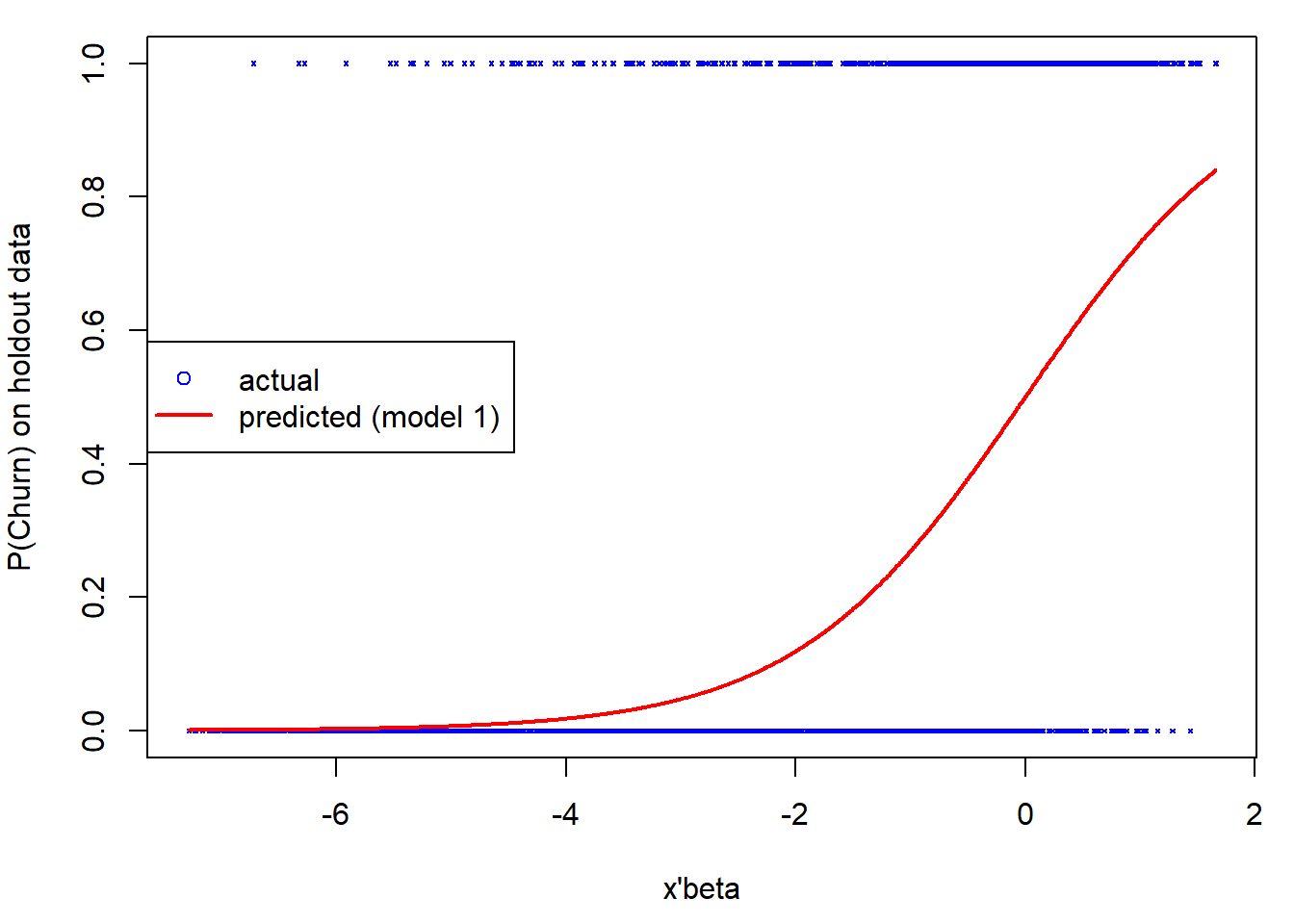
Now we use the model estimated on the other data to make predictions on this new data. Note that our predicted probabilities lie between 0 and 1, whereas our data are binary. We can get the predictions for each customer and graph them with the 0/1 churn decisions.

# predicted x'beta part of 
xb <- predict(model_1, type = "link", newdata=holdout_telco)
# the predicted probability 
prob <- predict(model_1, type = "response", newdata=holdout_telco)
head(cbind(xb,prob)) %>% 
  kbl() %>%
  kable_styling()

xb	prob
-3.715	0.024
-0.857	0.298
-1.460	0.188
-1.942	0.125
-5.194	0.006
-0.419	0.397

# order customers from least likely to churn (according to model) to most likely
ind <- order(prob)

Plot

par(mai=c(.9,.8,.2,.2))
plot(xb[ind],holdout_telco$Churn[ind], pch=4,cex=0.3,col="blue", xlab="x'beta",ylab="P(Churn) on holdout data")
lines(x=xb[ind], y=prob[ind], col="red", lwd=2)
legend('left',legend=c("actual", "predicted (model 1)"),col=c("blue","red"), pch=c(1,NA),lty=c(NA,1), lwd=c(NA,2))

Confusion matrix

We can also classify predictions by turning them into 0’s and 1’s. If \(\hat{p}_i > 0.5, \; \textrm{pred} = 1\) otherwise 0.

confusion_matrix <- (table(holdout_telco$Churn, prob > 0.5))
confusion_matrix <- as.data.frame.matrix(confusion_matrix)
colnames(confusion_matrix) <- c("No", "Yes")
confusion_matrix$Percentage_Correct <- confusion_matrix[1,]$No/(confusion_matrix[1,]$No+confusion_matrix[1,]$Yes)*100
confusion_matrix[2,]$Percentage_Correct <- confusion_matrix[2,]$Yes/(confusion_matrix[2,]$No+confusion_matrix[2,]$Yes)*100

print(confusion_matrix)

##     No Yes Percentage_Correct
## 0 1421  92               93.9
## 1  331 239               41.9

cat('Overall Percentage:', (confusion_matrix[1,1]+confusion_matrix[2,2])/nrow(holdout_telco)*100)

## Overall Percentage: 79.7

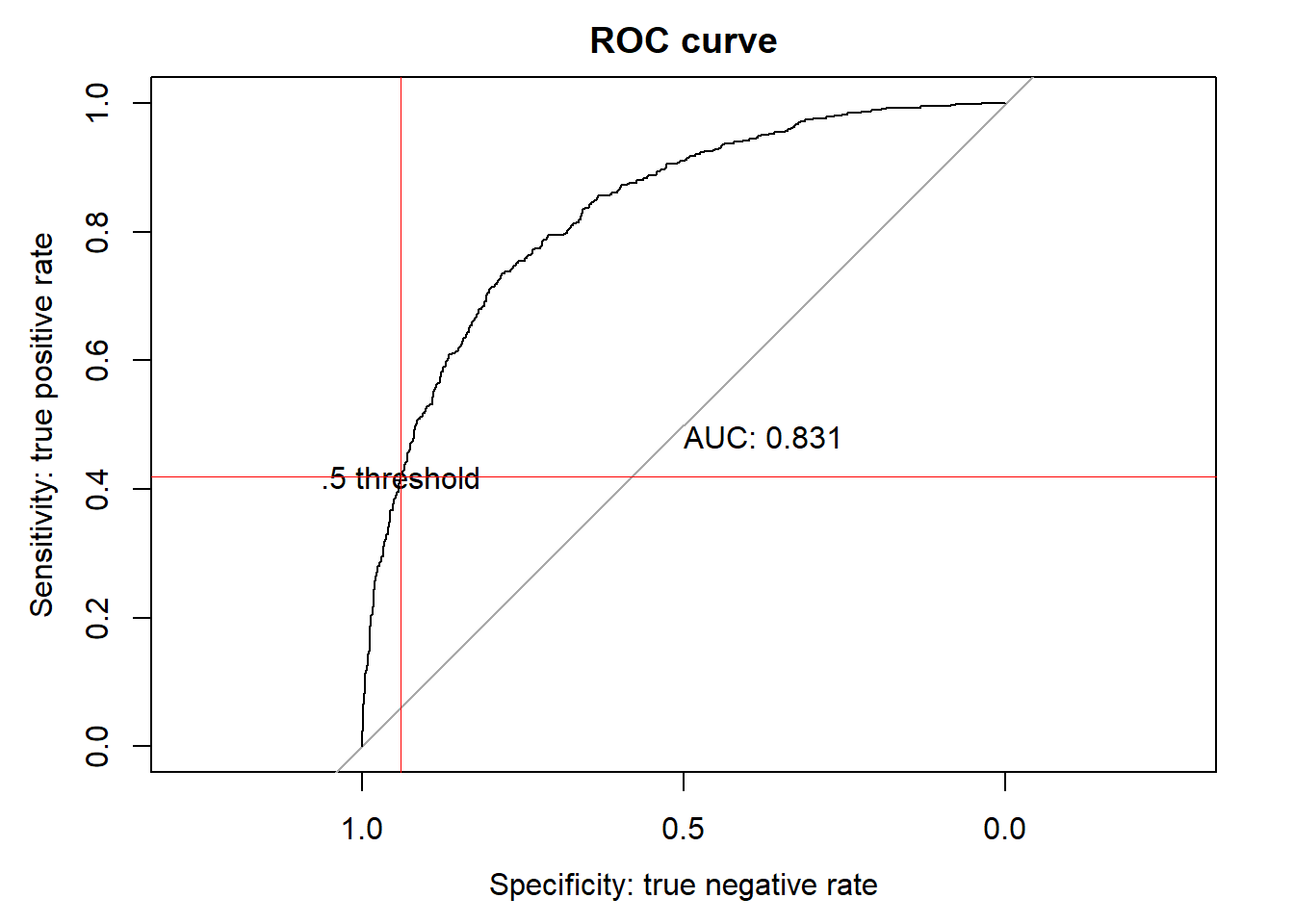
ROC curves

par(mai=c(.9,.8,.2,.2))
plot(roc(holdout_telco$Churn, prob), print.auc=TRUE, 
     col="black", lwd=1, main="ROC curve", xlab="Specificity: true negative rate", ylab="Sensitivity: true positive rate", xlim=c(1,0))
text(confusion_matrix$Percentage_Correct[[1]]/100, confusion_matrix$Percentage_Correct[[2]]/100, ".5 threshold")
abline(h=confusion_matrix$Percentage_Correct[[2]]/100, col="red",lwd=.3)
abline(v=confusion_matrix$Percentage_Correct[[1]]/100, col="red",lwd=.3)

Lift curves

Lift is a common measure in marketing of model performance. The lift asks how much more likely are customers in the top \(k^{\textrm{th}}\) decile to churn compared to the average.

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}
# create deciles
prob_decile = ntiles(prob, 10)

# prob, decile and actual
pred<-data.frame(cbind(prob,prob_decile, holdout_telco$Churn))
colnames(pred)<-c("predicted","decile", "actual")

# create lift table by decile
# average churn rate by decile

# lift is the actual churn rate in the decile divided by average overall churn rate
  
lift_table<-pred %>% group_by(decile) %>%  summarize(actual_churn = mean(actual), lift = actual_churn/rbar_ho, n_customers=n()) %>% arrange(desc(decile)) %>% mutate(cum_customers=cumsum(n_customers)) %>% mutate(cum_lift=cumsum(actual_churn)/sum(actual_churn)*100)

head(lift_table) %>% 
  kbl() %>%
  kable_styling()

decile	actual_churn	lift	n_customers	cum_customers	cum_lift
10	0.785	2.868	209	209	28.7
9	0.591	2.161	208	417	50.3
8	0.404	1.476	208	625	65.1
7	0.311	1.137	209	834	76.5
6	0.245	0.896	208	1042	85.4
5	0.139	0.510	208	1250	90.5

Customers in the top decile are the top 10% most likely to churn according to our model. The top decile lift is 2.868. Customers in the top decile are 2.868 times more likely to actually churn than the average customer.

The rightmost column shows the cumulative lift. The cumulative lift for the \(k\) decile is the percentage of all churners accounted for cumulatively by the first \(k\) deciles. The first decile contains 209% of all churners in the data set (in total there are 570 churners in the holdout dataset).

The cumulative lift of decile 2 is 208% of all churners are in the top 2 deciles. In the bottom most deciles there are barely any churners, so the cumulative lift increases little or not at all.

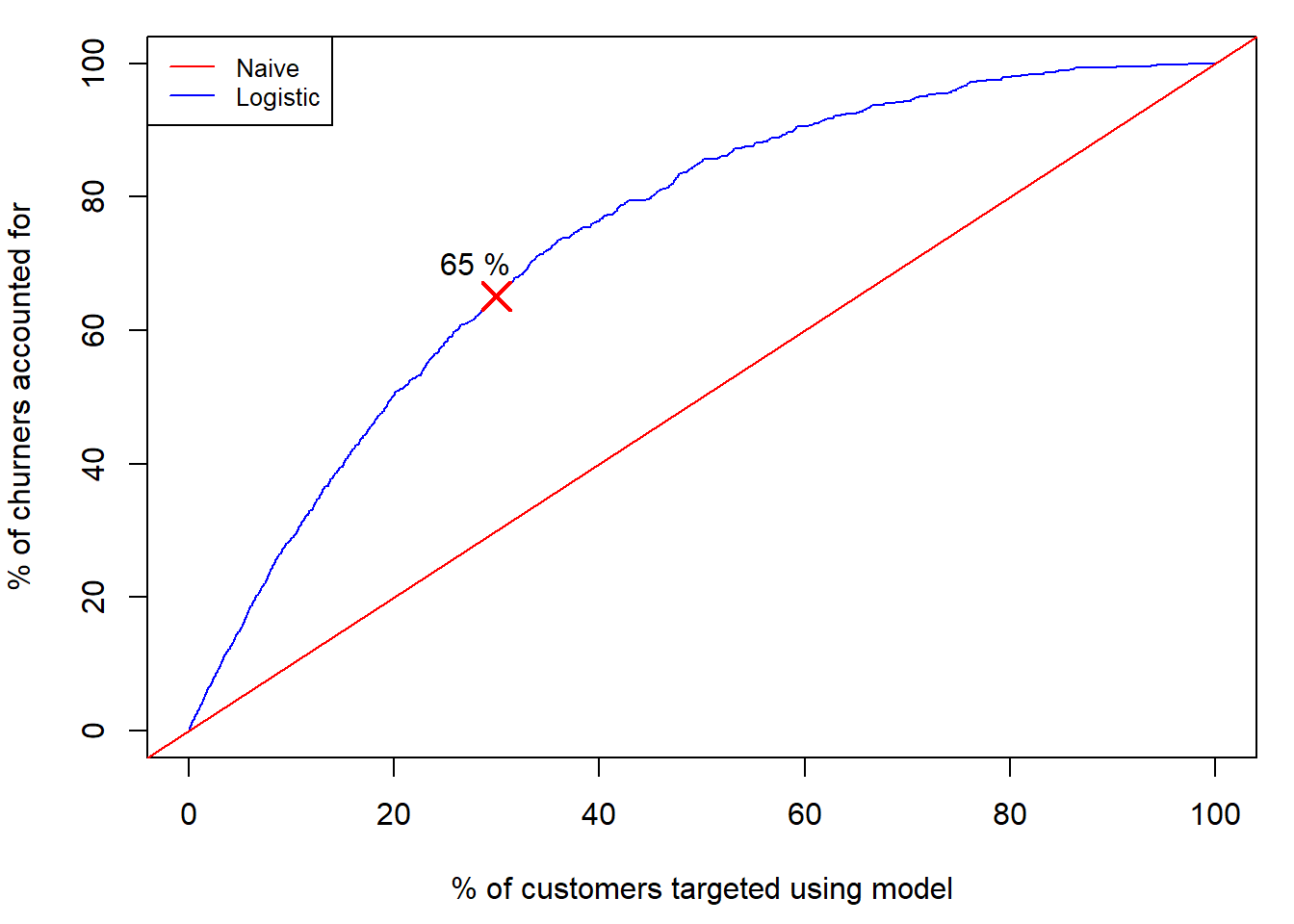
We can graph this out below. The top three deciles account for 208% of all churners. We can use this to compare models. The higher the lift for a given decile, the better the model. A straight line, where we randomly sorted customers instead of using a model, is the naive model.

# order from highest to smallest in terms of prob
# percentage of churners from beginning to end.
pred<-pred %>% arrange(desc(predicted)) %>% mutate(prop_churn = cumsum(actual)/sum(actual)*100, prop_cust = seq(nrow(pred))/nrow(pred)*100)
head(pred) %>% 
  kbl() %>%
  kable_styling()

	predicted	decile	actual	prop_churn	prop_cust
430	0.840	10	1	0.175	0.048
1887	0.840	10	1	0.351	0.096
320	0.821	10	1	0.526	0.144
811	0.820	10	1	0.702	0.192
179	0.817	10	1	0.877	0.240
88	0.814	10	1	1.053	0.288

# Plotting percentage of churners as a function of percentage of customers
par(mai=c(.9,.8,.2,.2))
plot(pred$prop_cust,pred$prop_churn,type="l",xlab="% of customers targeted using model",ylab="% of churners accounted for",xlim = c(0,100), ,ylim = c(0,100),col="blue")
legend('topleft', legend=c("Naive", "Logistic"), col=c("red", "blue"), lty=1:1, cex=0.8)
abline(a=0,b=1,col="red")
points(x=30, y= lift_table$cum_lift[3], pch=4, col="red",  cex=2, lwd=2)
text(x = 28,y= lift_table$cum_lift[3]+5, paste(round(lift_table$cum_lift[3],0), "%" ))

• This gives us equivalent information to the churn table.

• targeting the top 10% using the model would give us 28.772% of total churners in the data.

Selecting deciles to target

Once we have used the model to put customers in the right decile, targeting is simple. We calculate the profit from each n-tile and target customers who are in the profitable tiles. We will use the proactive churn framework from Blattberg, Kim and Neslin to calculate expected profits. This approach takes into account the actual proportion of churners as identified by the model.

The key parameter is \(\beta_K\), the proportion of churners in the top \(K\) deciles contacted.
\[ \beta_K = \frac{\sum_{k=1}^{K} \; r_k \, n_k}{\sum_{k=1}^{K} \; n_k} \quad \textrm{where} \; K = 1, 2, .. \dots, 10 \] We calculate \(\beta\), the probability that a targeted customer is a churner, by taking the cumulative proportion of churners in the top \(k\) deciles.

gamma = 0.1  # probability that customer is rescued if he or she is a churner
LTV = 500   # lifetime value of rescued customer
delta = 50  # cost of incentive
c = 0.50  # cost of contact

# re-order lift from highest to lowest
# add columns to our lift table

profit_table<-lift_table %>% mutate(
  cum_prop_churners = cumsum(actual_churn*n_customers)/cum_customers, 
  profit = cum_customers*((gamma*LTV+delta*(1-gamma))*cum_prop_churners-delta-c),
  decile=11-decile)
                                                                      
head(profit_table) %>% 
  kbl() %>%
  kable_styling()

decile	actual_churn	lift	n_customers	cum_customers	cum_lift	cum_prop_churners	profit
1	0.785	2.868	209	209	28.7	0.785	5026
2	0.591	2.161	208	417	50.3	0.688	6206
3	0.404	1.476	208	625	65.1	0.594	3682
4	0.311	1.137	209	834	76.5	0.523	-697
5	0.245	0.896	208	1042	85.4	0.467	-6356
6	0.139	0.510	208	1250	90.5	0.413	-14105

par(mai=c(.9,.8,.2,.2))
bp<-barplot(profit_table$profit ~ profit_table$decile, main="expected profits by # of deciles targeted", xlab="# deciles targeted", ylab="expected profits")

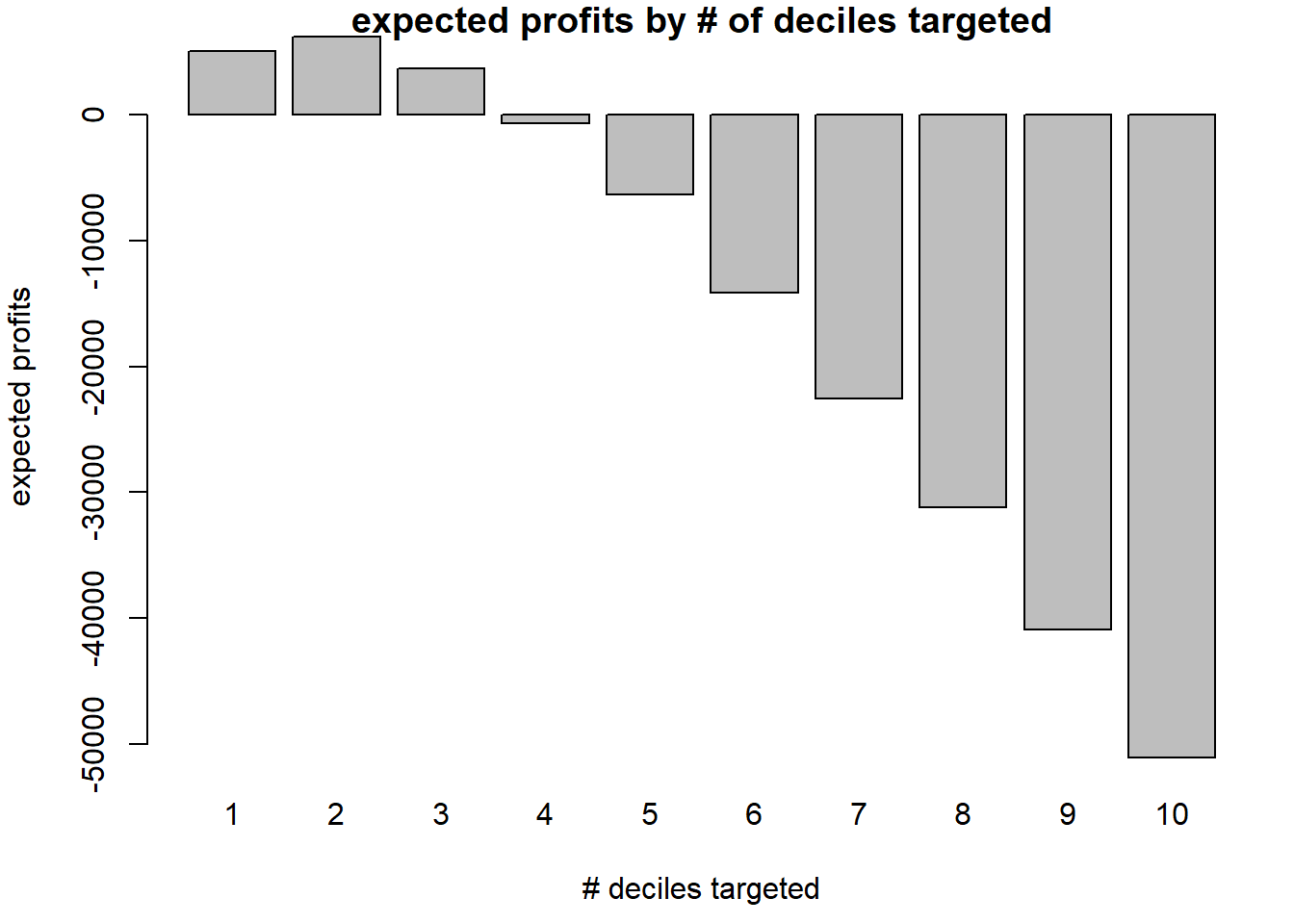
We see from the table below that given this model, the profit maximizing number of deciles to target is the top 2.