Tutorial 2: RFM Analysis

Data Import:

ebeer <- read_csv("ebeer.csv")

Introduction

RFM, recency (R), frequency (F) and monetary value (M) are the most often used database marketing metrics used to quantify customer transaction history. RFM analysis segments customer into groups according to these measures and relates these segments to the likelihood of responding to a marketing offer. This notebook discusses the measures, segmentation, usefulness for guiding marketing decisions, and extensions to the basic model.

Inspecting the data

Each row is a customer. acctnum is their id. We have gender, Recency (the number of months since the last purchase), Frequency (number of purchases), M (average amount spent per purchase), first purchase (number of months since first purchase), age, single, student, whether they received a mailing, did they respond.

head(ebeer)

## # A tibble: 6 × 11
##   acctnum gender     R     F     M firstpur age_class single student mailing respmail
##     <dbl>  <dbl> <dbl> <dbl> <dbl>    <dbl>     <dbl>  <dbl>   <dbl>   <dbl>    <dbl>
## 1   10001      1    30    10  35.7       50         3      1       1       1        0
## 2   10005      0    16     1 149         16         0      0       1       1        0
## 3   10010      0    12     1 123         12         0      1       0       1        0
## 4   10011      0     6     2 147          8         0      1       1       1        0
## 5   10014      1     6     3  96         18         0      0       1       1        1
## 6   10020      0    12     2 150.        14         0      1       1       1        0

Let’s look at the marketing variable: who gets a mailing in this dataset?

table(ebeer$mailing)

## 
##    0    1 
## 5012 4952

How many people of those mailed respond?

ebeer %>% 
  group_by(mailing) %>% 
  summarise(mean = mean(respmail), n = n())

## # A tibble: 2 × 3
##   mailing   mean     n
##     <dbl>  <dbl> <int>
## 1       0 NA      5012
## 2       1  0.124  4952

Binomial model for responses

The probability of observing \(s\) people respond out of \(n\) people mailed is described by a binomial distribution: \[P(s|n, p) = {n \choose s} p^{s} (1-p)^{n-s}\]

The overall response rate (probability of response) is \(\hat{p}=\) 0.124, and the standard error is 0.005.

ci_low <- qnorm(0.025, mean=p_hat, sd=p_hat_se) 
ci_high <- qnorm(0.975, mean=p_hat, sd=p_hat_se) 

## The Response Rate is Between 0.115 and 0.134

The confidence interval is [0.115; 0.134].

Creating R, F and M segments separately.

Let’s look at the distribution of raw RFM variables.

ebeer$F <- as.numeric(ebeer$F)
par(mai=c(.9,.8,.2,.2))
hist(ebeer$R, main="Recency", xlab="Recency: # months since last purchase")

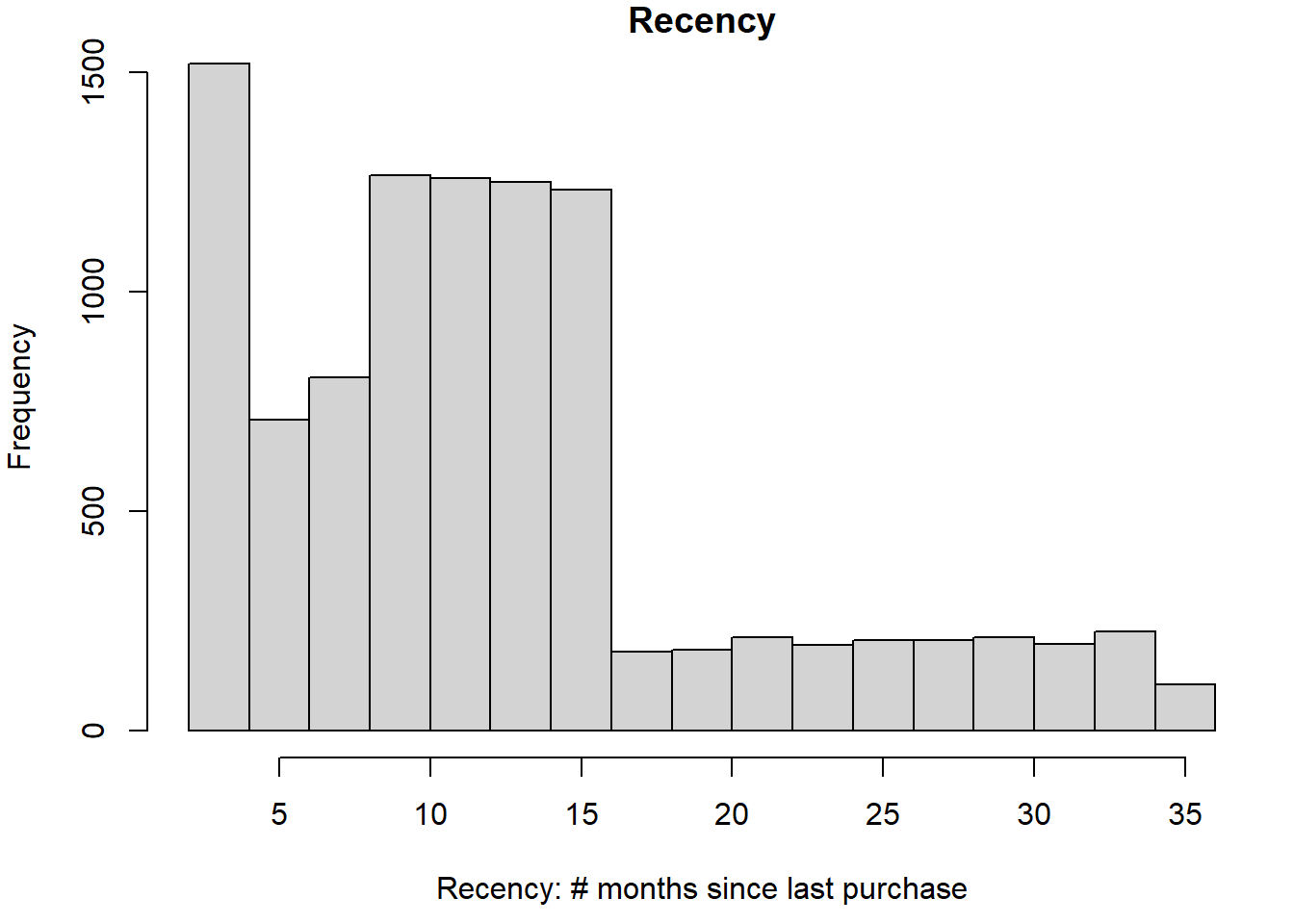
hist(ebeer$F, main="Frequency", xlab="Frequency: # purchases")

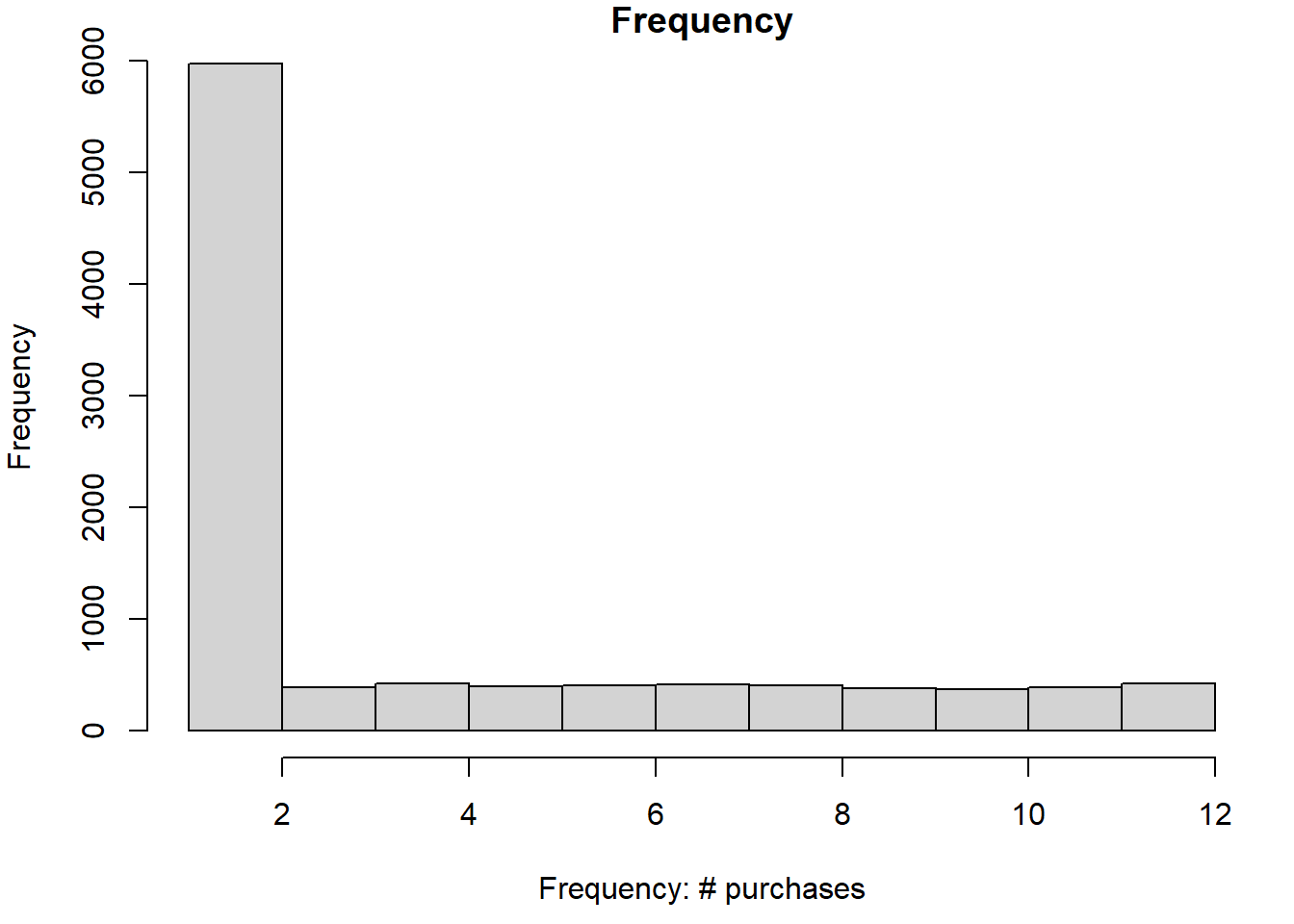
hist(ebeer$M, main="Monetary", xlab="Monetary: avg amount spent per purchase")

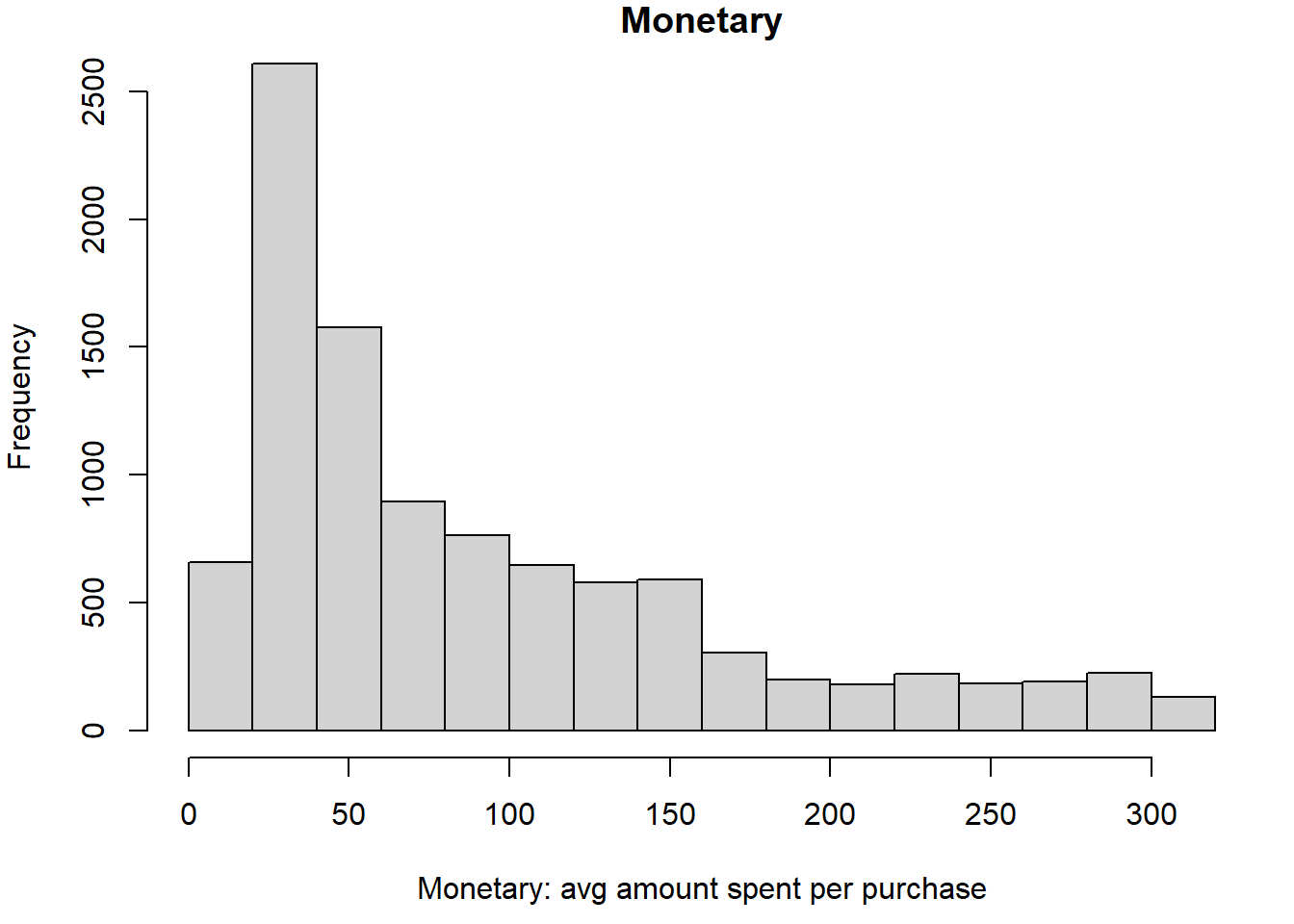
Let’s first create segments from each variable separately; we create separate segments for R, F, and M. We sort them from largest to smallest. Then we create \(n\) bins, where \(n=5\)

We do this by creating quantiles, divide into 20% most recent, 20% next most recent. We use the quantcut function in package rtools.

ebeer$Rgroup <- quantcut(x = ebeer$R, q=5)

ebeer %>% 
  group_by(Rgroup) %>% 
  summarise(n=n(), mean_R=mean(R), sd_R=sd(R))

## # A tibble: 5 × 4
##   Rgroup      n mean_R  sd_R
##   <fct>   <int>  <dbl> <dbl>
## 1 [2,6]    2229   3.97 1.62 
## 2 (6,10]   2069   9.22 0.975
## 3 (10,14]  2509  13.0  1.00 
## 4 (14,16]  1231  16    0    
## 5 (16,36]  1926  26.8  5.46

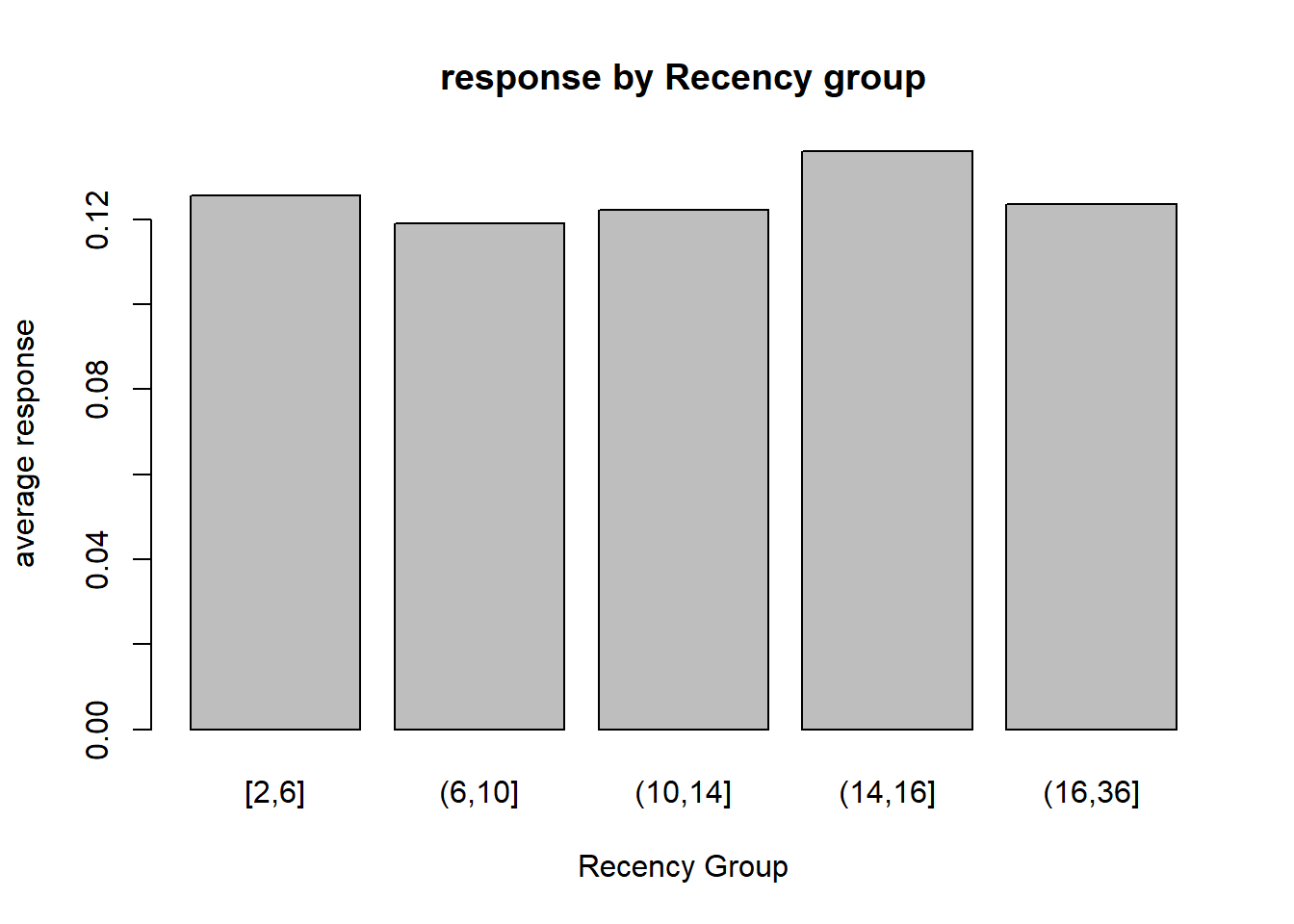
Now, let’s examine how response rate vary with the recency groups we just created. We only want to look at the subset of customer who were mailed, so we filter the dataset first filter(mailing==1). We group by our just created 5 R segments. And we calculate the mean of response, mean(respmail).

respR <- ebeer %>% 
  filter(mailing==1) %>% 
  group_by(Rgroup) %>% 
  summarise(avg_respmail=mean(respmail), sd_respmail=sd(respmail), n=n())
respR

## # A tibble: 5 × 4
##   Rgroup  avg_respmail sd_respmail     n
##   <fct>          <dbl>       <dbl> <int>
## 1 [2,6]          0.126       0.332  1098
## 2 (6,10]         0.119       0.324  1041
## 3 (10,14]        0.122       0.328  1211
## 4 (14,16]        0.136       0.343   632
## 5 (16,36]        0.124       0.329   970

barplot(respR$avg_respmail~respR$Rgroup, main="response by Recency group", xlab="Recency Group", ylab="average response")

Full RFM analysis

Now do the full RFM analysis. Remember, the idea is that

1. We first sort by R, create segments. (we already did this.)
2. Within each R segment, we sort F and create RF segments.
3. Within each RF segment, we sort M and create RFM segments.

The way to do this is slightly complicated; I would give you this script in an exam or assignment. You would not have to code this up yourselves. First, we change ebeer into data.table Within each R group, we create F groups -> RF groups. Within each RF group, we create M groups -> RFM groups

ntiles <- function(x, bins) {
  quantiles = seq(from=0, to = 1, length.out=bins+1)
  cut(ecdf(x)(x),breaks=quantiles, labels=F)
}

ebeer$Rgroup <- ntiles(ebeer$R, bins=5)  


dt = data.table(ebeer)
nbins = 5
dt[, RFgroup := paste0(as.character(Rgroup), as.character(ntiles(F, bins = nbins))), by = c('Rgroup')]
dt[, RFMgroup := paste0(as.character(RFgroup), as.character(ntiles(M, bins = nbins))), by = c('RFgroup')]

# put it back to data.frame
ebeer = data.frame(dt)

# change it to a factor variable
ebeer$RFMgroup <- as.factor(ebeer$RFMgroup)

How many RFM groups do we get with this procedure?

length(unique(ebeer$RFMgroup))

## [1] 90

We have 90 RFM segments.

barplot(table(ebeer$RFMgroup), xlab = "RFM segments", ylab="frequency")

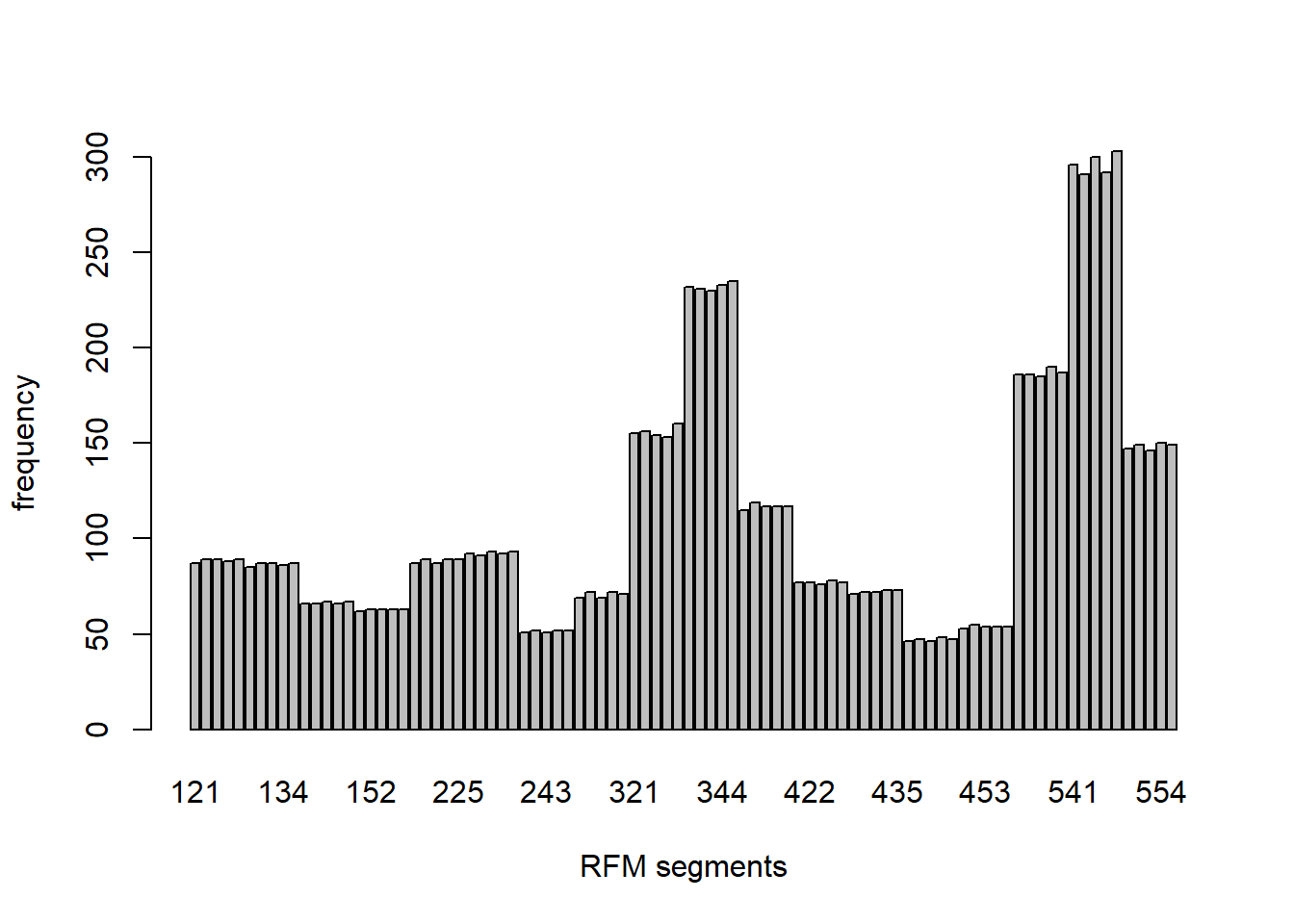
Response rate by RFM segment

Let’s make the response rate by segment.

# p = s_z/n_z
respRFM <- ebeer %>% 
  group_by(RFMgroup) %>% 
  summarise(n_resp= sum(respmail, na.rm = TRUE), 
            n_mail= sum(mailing, na.rm = TRUE)) %>% 
  mutate(resp_rate = n_resp/n_mail) %>% 
  arrange(desc(resp_rate)) #re-order from most to least, make picture better
respRFM

## # A tibble: 90 × 4
##    RFMgroup n_resp n_mail resp_rate
##    <fct>     <dbl>  <dbl>     <dbl>
##  1 454          14     28     0.5  
##  2 453           9     20     0.45 
##  3 441           8     18     0.444
##  4 152          12     29     0.414
##  5 151          13     33     0.394
##  6 252          13     33     0.394
##  7 154          11     28     0.393
##  8 155          11     28     0.393
##  9 451          11     28     0.393
## 10 555          30     77     0.390
## # … with 80 more rows

Targeting using RFM analysis

Now let’s figure out which segments we should target. We want to target segments that have a response rate above the breakeven point. Remember the breakeven probability: \[ \bar{p}_{BE} = \frac{c}{m} = \frac{\textrm{cost}}{\textrm{margin}} \]

c = 1.5
m = 50
brk = c/m

Our breakeven point is 0.03.

respRFM <- as.data.frame(respRFM)

bp <- barplot(respRFM[,4], 
              main="response by RFM group", 
              xlab="RFM Group", ylab="average response", xaxt="n")
axis(1, at = bp[,1], labels=respRFM[,1], cex.axis=0.7, las=2)

abline(h=brk)
text(85, brk, "breakeven", cex=1, pos=3, col="black")

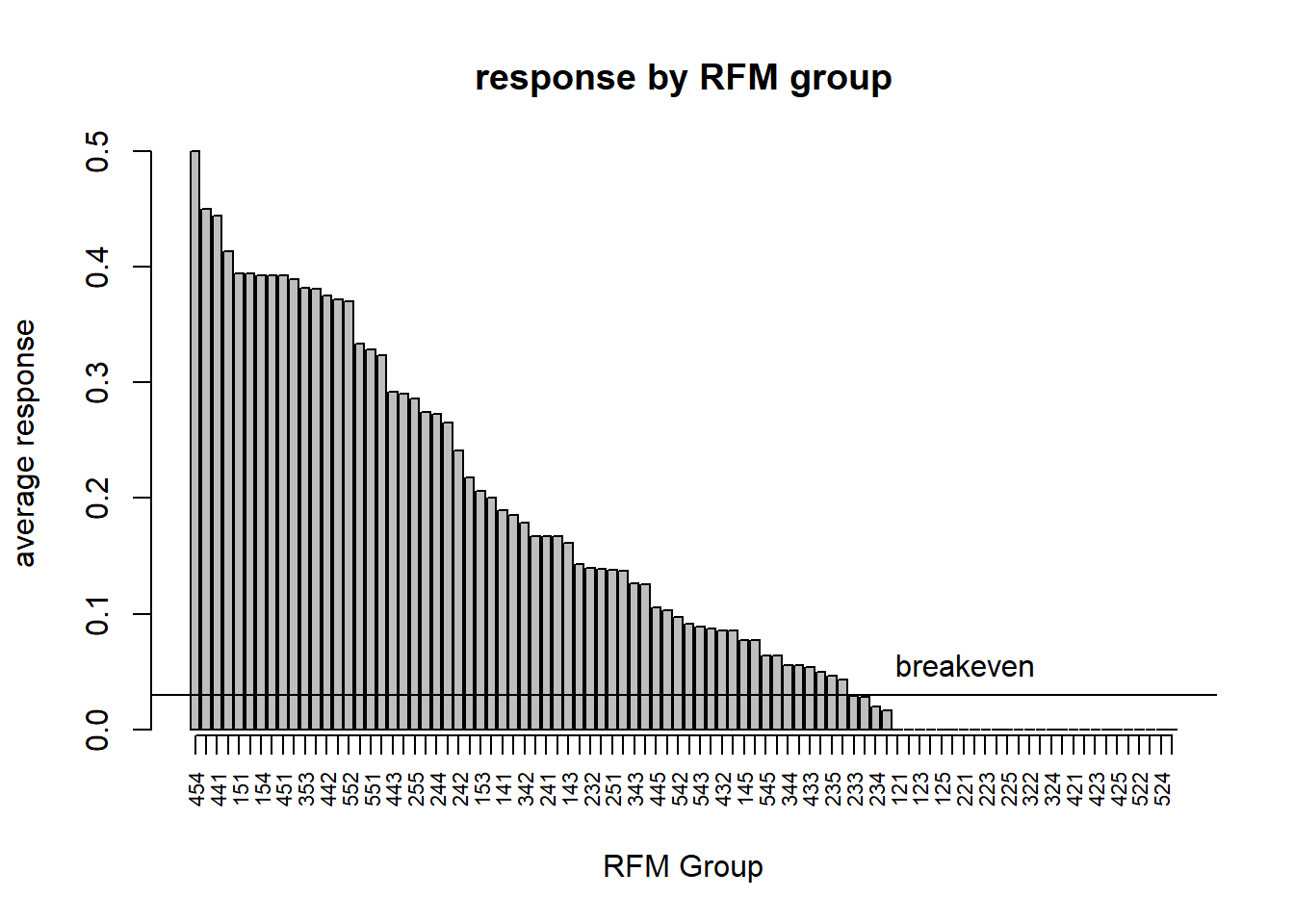
How many segments are above the breakeven, and therefore targeted? What segments are they? As a percentage of the total segments?

# how many segments above breakeven? which segments?
n_segments <- sum(respRFM$resp_rate >= brk)
# as a percentage of all segments
p_segments <- sum(respRFM$resp_rate >= brk) / length(unique(ebeer$RFMgroup))

## Optimal Number of Segments to target is 60 which is 66.7 % of total segments

Prediction of Rollout Customers

OK, now let’s apply this model to those customers who have not been mailed, sometimes called the “rollout” sample. We use binary linear regressions to predict. The \(\hat{\beta}_z\) will be the mean response rate of each segment.

RFM_model <- lm(respmail ~ RFMgroup, data = ebeer)

Applying predictions to rollout data: ROI

We separate the rollout data (where there is no mailing) from everything else. Then, we’ll score the new data, i.e., apply the predictions of the model to the new data.

ebeer.rollout <- ebeer[is.na(ebeer$respmail), ]

##Prediction
ebeer.rollout$RFMpred <- predict(RFM_model, ebeer.rollout)

summary(ebeer.rollout$RFMpred)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   0.000   0.000   0.085   0.125   0.185   0.500

The average prediction is the average response rate we found earlier. So makes sense in terms of face validity.

We now have a probability of response to everyone in the rollout data. How many customers in the rollout would get mailed? as a fraction of the total, what would the profits and return on investment (ROI) be?

# Total number of rollout customers with predicted response rates above breakeven
n_customers <- sum(ebeer.rollout$RFMpred >= brk)
# as a proportion of all rollout customers
p_customers <- sum(ebeer.rollout$RFMpred >= brk) / length(ebeer.rollout$RFMpred)

## Optimal Number of Segments to target is 3222 which is 64.3 % of total segments

# profit per customer
# if p > p_BE, expected profit = p*m - c  ||  if p < p_BE, = 0
ebeer.rollout <- ebeer.rollout %>% 
  mutate(RFMprofit = case_when(RFMpred >= brk ~ RFMpred*m-c, 
    TRUE ~ 0))
# or pmax takes columnwise maximum (same as in L2)
#ebeer.rollout$RFMprofit <- pmax(ebeer.rollout$RFMpred *m - c, 0)

# sum over customers
sum_profit = sum(ebeer.rollout$RFMprofit)

# sum costs of targeting customers
ebeer.rollout$RFMcost <- ifelse(ebeer.rollout$RFMpred >= brk, c, 0)

sum_cost = sum(ebeer.rollout$RFMcost)

## ROI: 540 %

If we targeted everyone in the rollout group:

ebeer.rollout$all <-ebeer.rollout$RFMpred *m - c
sum_profit_all = sum(ebeer.rollout$all)
sum_cost_all = c*length(ebeer.rollout$RFMpred)

## ROI: 315 %

respRFM <- respRFM %>% mutate(n_nonresp = n_mail-n_resp) %>% relocate(n_nonresp, .after=n_resp)

Using a Bayesian approach

Right now we assume that these segments response rates are entirely independent of each other. But if we make an assumption about the distribution of response rates across segments, we could use that common distribution to “borrow” information from the other segments.

par(mai=c(.9,.8,.2,.2))
hist(respRFM$resp_rate, density=10, breaks=20, main="Distribution of response rates across segments", xlab="segment-specific probability of response")
curve(dbeta(x, .3, 3), add = TRUE,  type="l", col="gray")

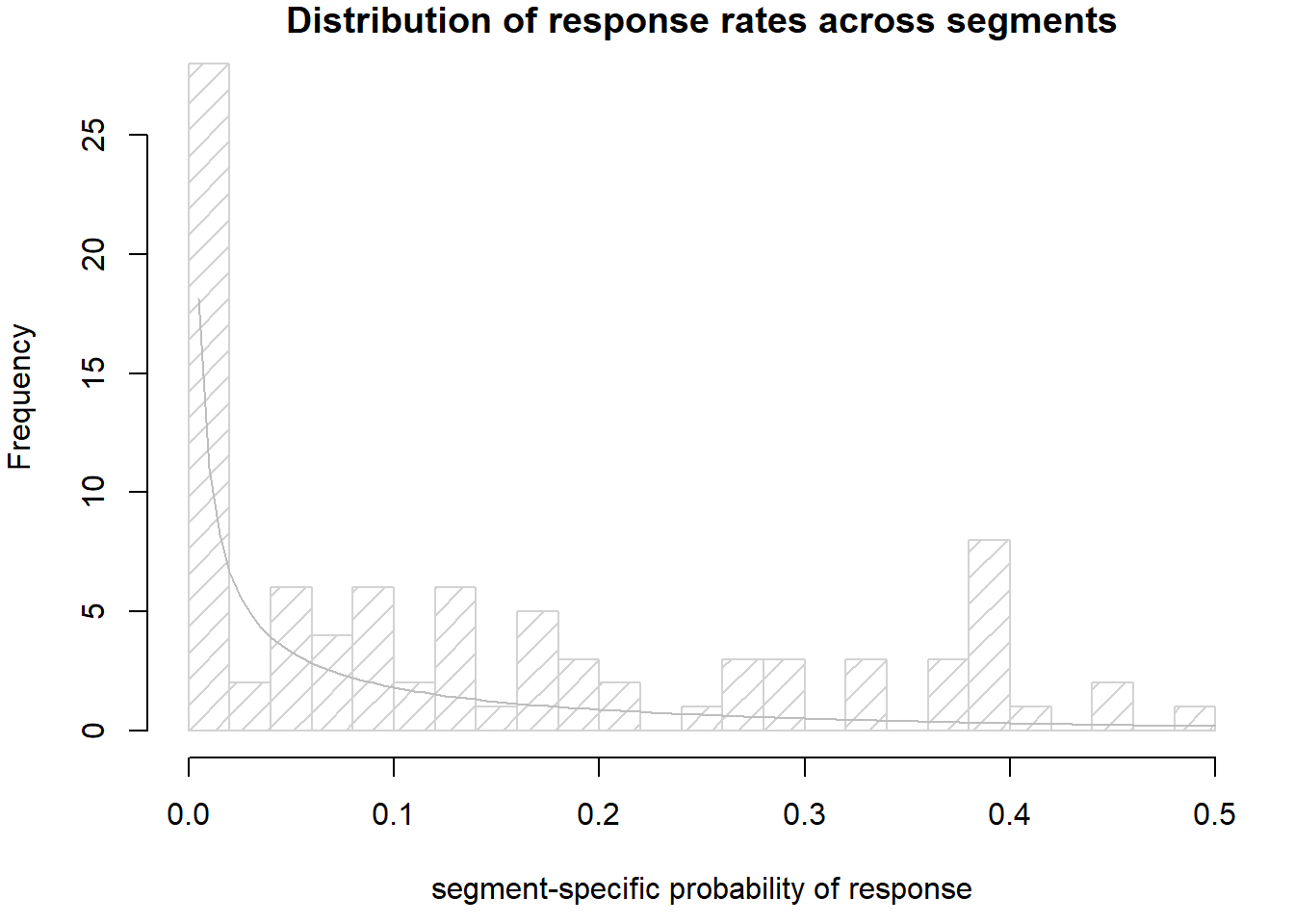
Empirical Bayes

\[ \begin{array}{ccl} P(s_z|n_z, a, b)& = & \displaystyle {n_z \choose s_z} \frac{B(a+s_z,b+n_z-s_z)}{B(a,b)} \end{array} \] #### Prior We start by estimating the priors borrowing information form other segments. We use MLE for this:

Coef(fit)

## shape1 shape2 
##  0.493  3.113

# make them a and b
a <- Coef(fit)[[1]]
b <- Coef(fit)[[2]]

Let’s plot this prior estimate against the data

par(mai=c(.9,.8,.2,.2))
hist(respRFM$resp_rate, density=10, breaks=20, main="Distribution of response rates across segments", xlab="segment-specific probability of response")
curve(dbeta(x, a, b), add = TRUE,  type="l", col="red")
curve(dbeta(x, .3, 3), add = TRUE,  type="l", col="blue")

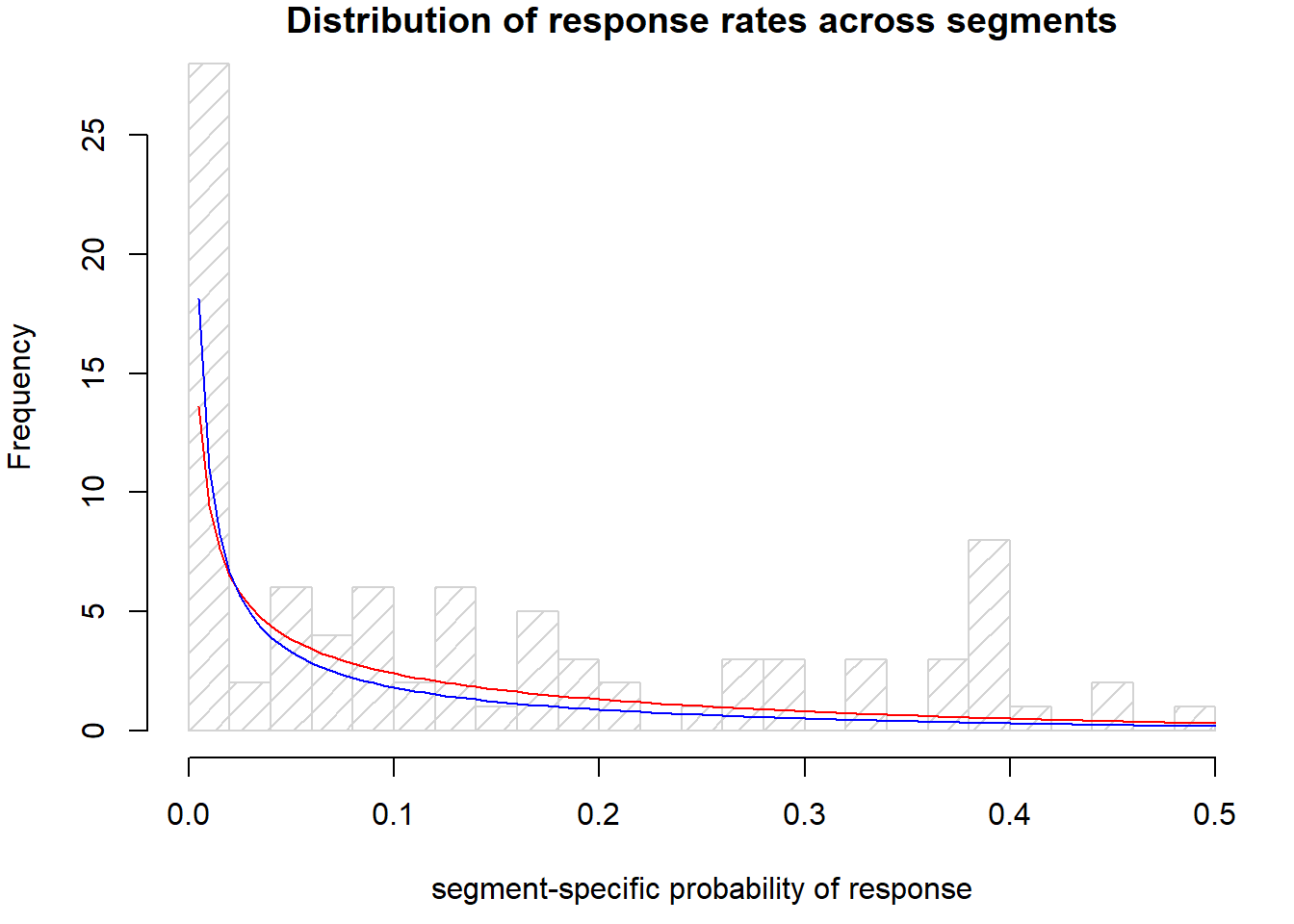
Posterior Mean Response

# posterior mean response rate
post_mean_resp <- (a+respRFM$n_resp)/(a+b+respRFM$n_mail)
             
# add this as column to respRFM
respRFM <- cbind(respRFM, post_mean_resp)

#order from lowest to greatest
respRFM <- respRFM %>% arrange((resp_rate))

head(respRFM)

##   RFMgroup n_resp n_nonresp n_mail resp_rate post_mean_resp
## 1      121      0        39     39         0        0.01157
## 2      122      0        48     48         0        0.00955
## 3      123      0        46     46         0        0.00994
## 4      124      0        45     45         0        0.01014
## 5      125      0        38     38         0        0.01185
## 6      131      0        43     43         0        0.01058

We plot this:

plot(respRFM$resp_rate, xaxt="n",col="red",xlab="RFM segments",ylab="response rate (x/n) and posterior mean response rate")
points(respRFM$post_mean_resp, col='blue')
legend('topleft',legend=c("estimate response rate", "posterior expected response rate"),col=c("red","blue"), pch=1)
axis(1, at = 1:90, labels=respRFM$RFMgroup, cex.axis=0.7, las=2)
abline(h=brk)
text(85, brk, "breakeven", cex=1, pos=3, col="black")

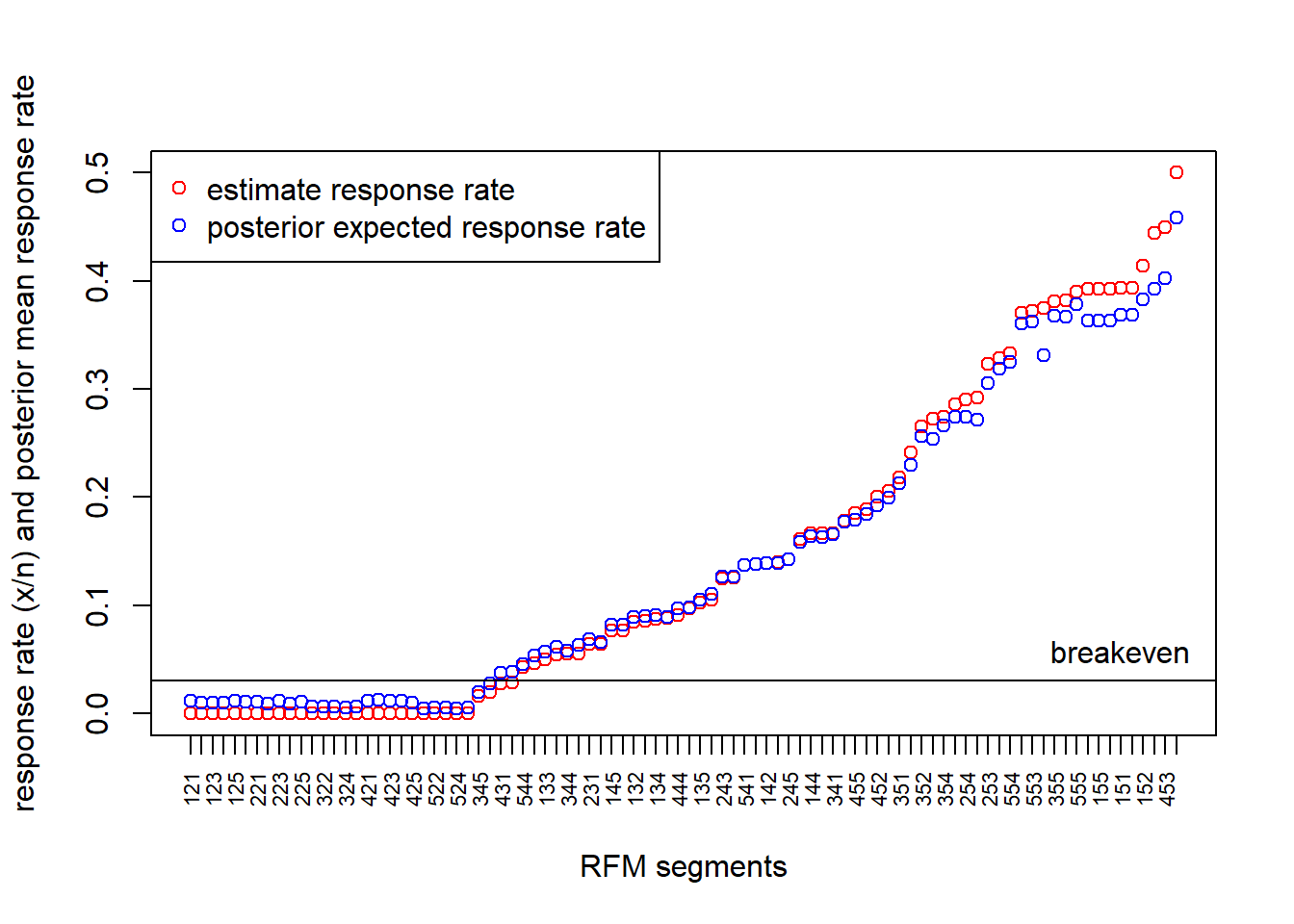
Are there any switches we would make using the posterior mean rather than the actual mean to target segments?

## Using the posterior mean to target segments leads to 62 segments, whereas using the actual mean leads to 60