Tutorial 1: Test & Roll

We now can upload our data.

ebeer <- read_csv("ebeer.csv")

Set the seed so that random draws are the same for everyone

set.seed(19312)

Exploratory Data Analysis

How many observations, how many variables? Show the first 10 observations

head(ebeer) %>% select(-acctnum) %>% 
  kbl() %>%
  kable_styling()

gender	R	F	M	firstpur	age_class	single	student	mailing	respmail
1	30	10	35.7	50	3	1	1	1	0
0	16	1	149.0	16	0	0	1	1	0
0	12	1	123.0	12	0	1	0	1	0
0	6	2	147.0	8	0	1	1	1	0
1	6	3	96.0	18	0	0	1	1	1
0	12	2	150.5	14	0	1	1	1	0

Table: Summary Statistics

st(ebeer[-1], summ=c('mean(x)', 'sd(x)', 'min(x)', 'max(x)'))

Summary Statistics

Variable	Mean	Sd	Min	Max
gender	0.3	0.458	0	1
R	13.2	8.117	2	36
F	3.9	3.471	1	12
M	92	75.449	15	314
firstpur	26.5	18.216	2	99
age_class	0.9	1.103	0	8
single	0.3	0.461	0	1
student	0.5	0.499	0	1
mailing	0.5	0.5	0	1
respmail	0.1	0.33	0	1

Monetary Value

Let’s plot the distribution of the monetary amount spent by our customers (M) . This is the monetary value.

ebeer %>% 
  ggplot(aes(x = M)) + 
  geom_histogram(bins = 100, colour = "black", fill = "#00A087B2") +
  xlab("Monetary amount") + ylab("Frequency") +
  theme_bw()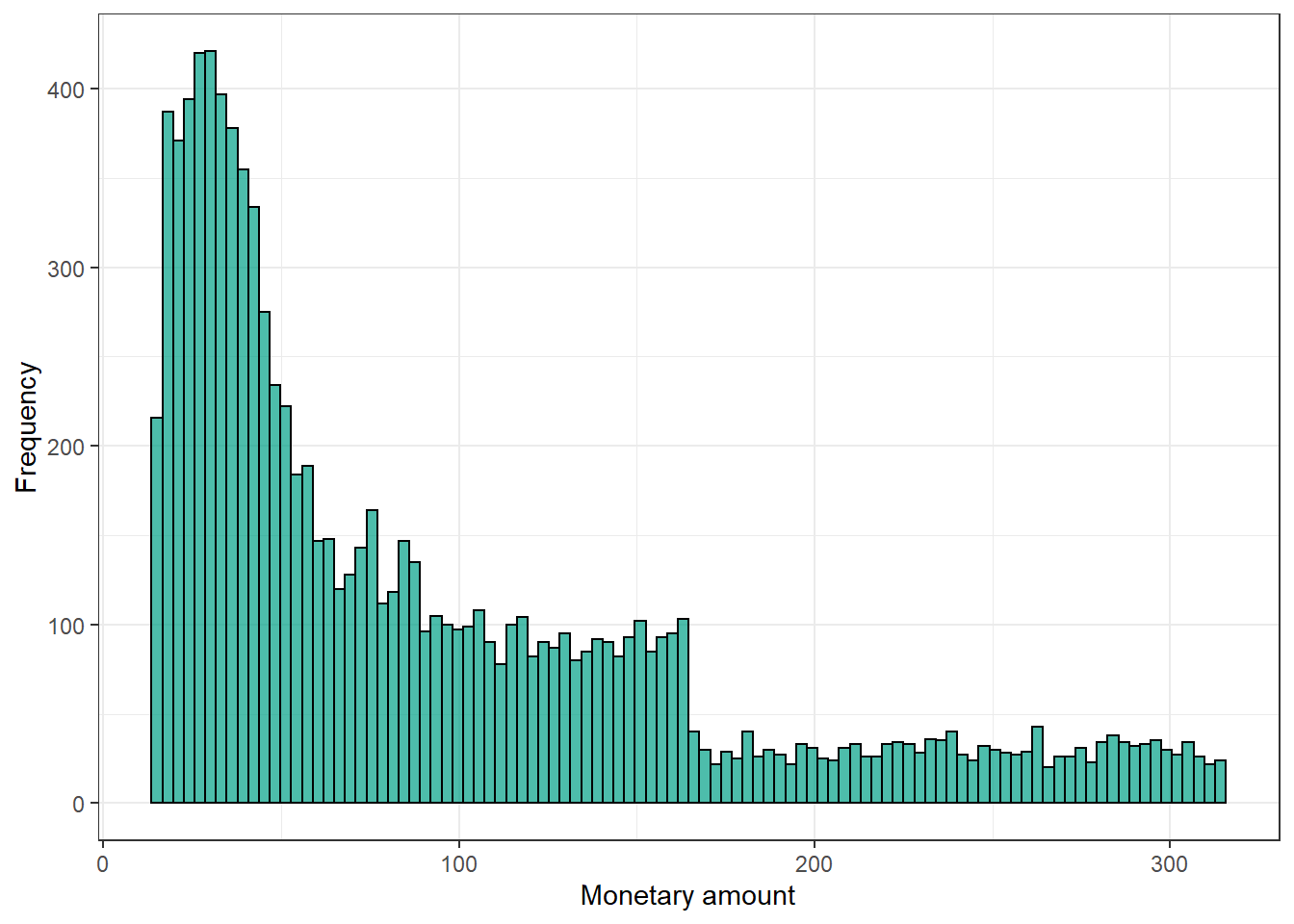

How does average amount spent (M) and its standard deviation vary by whether customers responded to the mailing?

ebeer %>% 
  group_by(respmail) %>% 
  summarise(N = n(), Mean = round(mean(M),2), Std.Dev = round(sd(M),2)) %>% 
  kbl() %>%
  kable_styling()

respmail	N	Mean	Std.Dev
0	4336	98.7	77.0
1	616	42.2	26.9
NA	5012	92.3	75.8

Uncertainty

Classical Uncertainty: Normal Distribution

Let’s estimate the distribution of the monetary amount, assuming normal distribution:

xbar <- mean(ebeer$M) 
xbse <-  sqrt(var(ebeer$M)/nrow(ebeer))

We can also plot the sampling distribution of the sample mean, assuming Normal Distribution:

norm.density <- as.data.frame(cbind(xx, m=dnorm(xx, xbar, xbse))) 

norm.density %>% 
  ggplot(aes(xx, m)) +
  geom_line(color = "#00A087B2") +
  geom_vline(aes(xintercept=xbar), color="black", linetype="dashed") +
  xlab("Average Monetary Value") + ylab("Density") +
  theme_bw()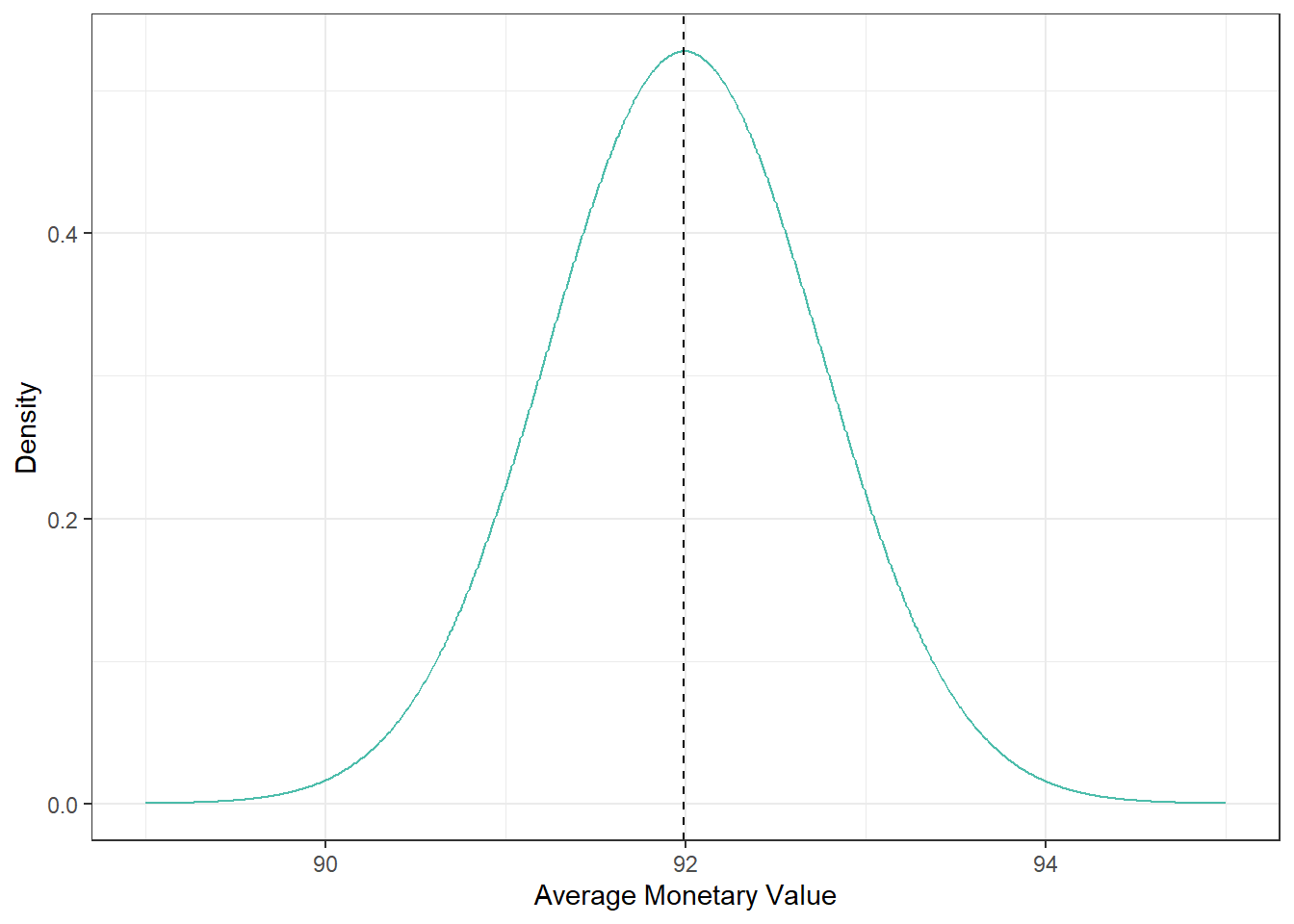

Classical Uncertainty: Nonparametric Bootstrap

Another way to compute the distribution is using the bootstrap.

# nonparametric bootstrap
B <- 10000 # number of bootstrap samples
mub <- c() # where we are going to collect the mean
set.seed(19312) # setting seed right before sampling
for (b in 1:B){
  samp_b = sample.int(nrow(ebeer), replace=TRUE) # sample with replacement
  mub <- c(mub, mean(ebeer$M[samp_b])) # store the mean of the sample 
}

Let’s build a Comparison Table:

Distribution Comparison

	Mean	Std. Dev.	Confidence Intervals (95%)
Normally Distributed	91.993	0.756	[90.512; 93.475]
Nonparametric Bootstrap	91.989	0.756	[90.507; 93.471]

The final Plot with the distribution of the bootstrapped mean:

as.data.frame(mub) %>% 
  ggplot(aes(mub)) + 
  geom_histogram(aes(y=..density..), bins = 100, colour = "black", fill = "#00A087B2") +
  geom_density(color="#3C5488B2", size=1) +
  geom_vline(aes(xintercept=mean(mub)), color="black", linetype="dashed", size=1) +
  xlab("Average Monetary Value") + ylab("Density") +
  theme_bw()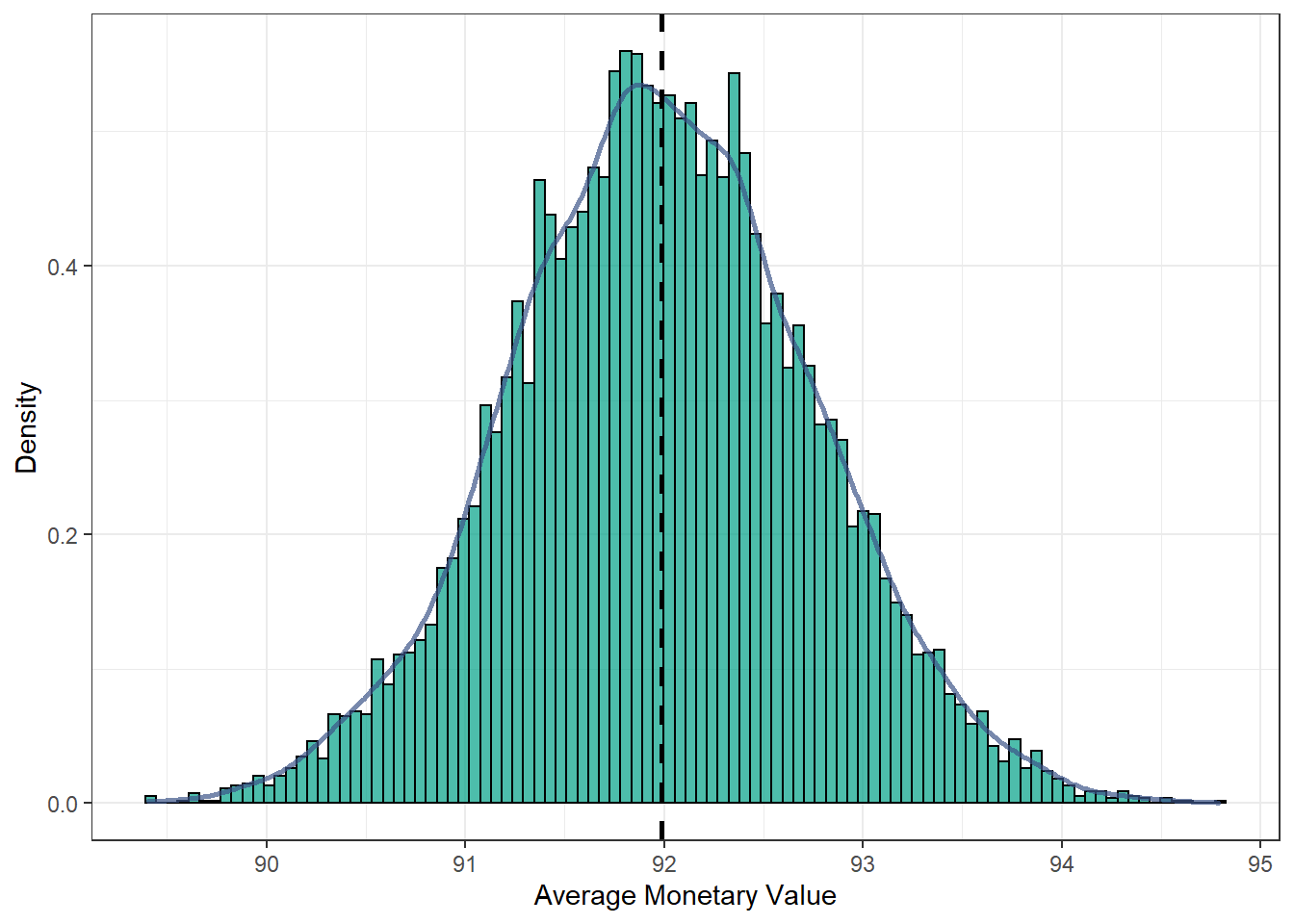

We can compare both distributions:

as.data.frame(mub) %>% 
  ggplot(aes(mub)) + 
  geom_density(color="#3C5488B2") +
  geom_line(data = norm.density, aes(xx, m) , color = "#00A087B2") +
  geom_vline(aes(xintercept=mean(mub)), color="blue", linetype="dashed") +
  geom_vline(aes(xintercept=xbar), color="black", linetype="dashed") +
  xlab("Average Monetary Value") + ylab("Density") +
  theme_bw()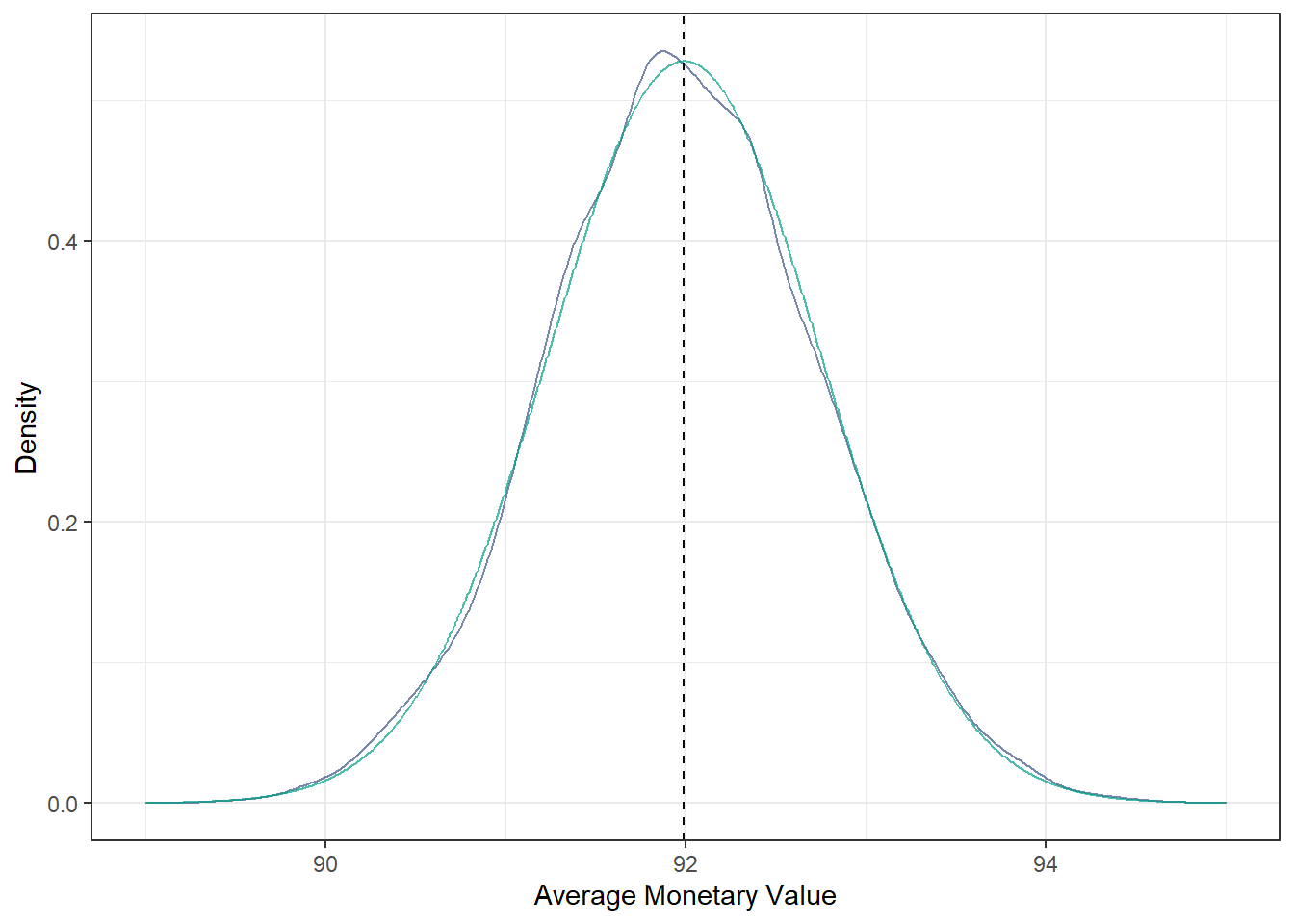

Bayesian Uncertainty

A. Binary Example

Let’s consider the class example of an emailing campaign and we want to know the uncertainty of the response rates \(p\). One way to measure uncertainty of the possible values of the response rate is to assume that \(p\) comes from a beta distribution. The mean of the beta distribution is \[E[p|a,b]=\frac{a}{a+b}\]

Prior

## The mean response rate is 0.027

In our case, we have some prior that the response rate is 0.027, so that we can plot the prior distribution.

xx=seq(0,1,length=1000)

plot(xx, y=dbeta(xx, shape1=prior_a, shape2 = prior_b), 
     type="l", col="black", xlab="Response Rate", ylab="Prior Density")
abline(v=prior_a/(prior_a+prior_b))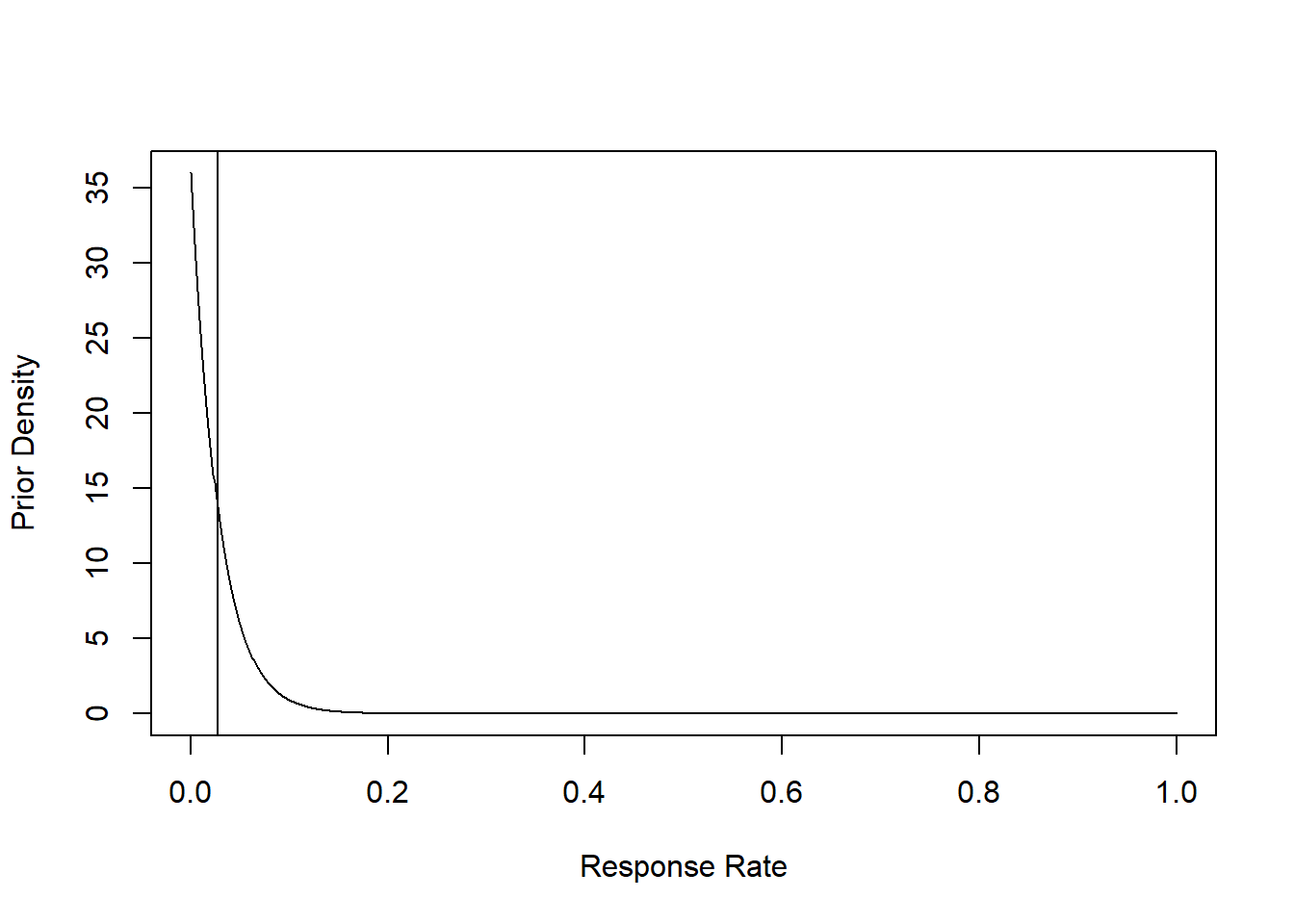

Posterior

Bayes rule tells you how you should update your beliefs after you see some data.

\[ \textrm{posterior} \propto \textrm{likelihood} \times \textrm{prior} \]

Now, we already assume some prior and now we run the experiment and we see our data results. With this, we can update our prior belief by calculating the posterior. Our observed experiment had the following characteristics:

n = 5000 # number in test sample
s = 175 # number of responses | (s) Number of Successes vs. (n-s) Number of Failures
c = 1.5 # cost per mailing
m = 50 # profit if respond

We can calculate the probability that the posterior is above the breakeven point: \[ p >\frac{c}{\pi} \equiv \frac{1.5}{50} = 0.03 \]

So that we are interested in: \[ \Pr(p<0.03) \] We estimate the probability by drawing from a beta distribution with above parameters.

B = 10000 # number draws from distribution

prior_a = 1
prior_b = 36
post_a= prior_a + s
post_b = prior_b + n - s

xx=seq(0,.07,length=1000)

plot(xx, y <- dbeta(xx, shape1=post_a, shape2 = post_b), 
     type="l", col="black", xlab="Response Rate", ylab="Posterior Density")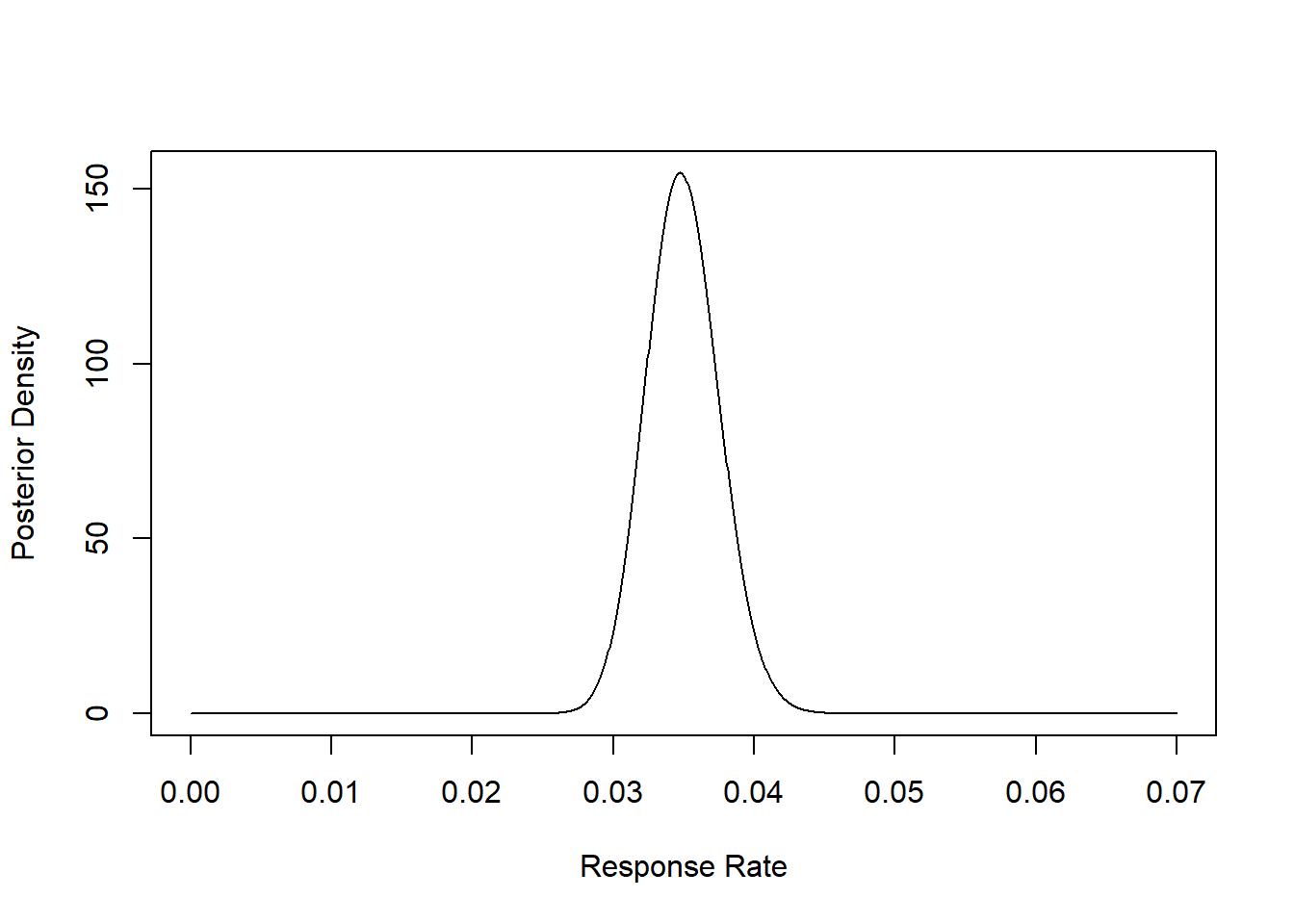

The Mean Posterior Response Rate:

## The mean response rate is 0.035

95% Confidence Interval:

prior_ci <- round(qbeta(c(0.025, 0.975), shape1=prior_a, shape2 = prior_a),3)
posterior_ci <- round(qbeta(c(0.025, 0.975), shape1=post_a, shape2 = post_b),3)

## Prior Response Rate 95% CI: 0.025 0.975

## Posterior Response Rate 95% CI: 0.03 0.04

Probability of Passing Breakeven Point:

set.seed(19312)
post_draws <- rbeta(B,post_a,post_b) #random deviates

## The Probability that the response rate is above the breakeven point is 0.023

Prior vs Posterior:

plot(xx, y=dbeta(xx, shape1=post_a, shape2 = post_b), 
     type="l", col="black", xlab="Response Rate", ylab="Posterior Density")
lines(xx, y=dbeta(xx, shape1=prior_a, shape2 = prior_b), type="l", col="gray")
abline(v=brk)
legend("topright", col=c("black", "gray"), legend=c("posterior", "prior"), bty="n", lty=1)
set.seed(19312)
prob = sum(post_draws<brk)/B
text(x = .02,y= 100, paste("P(p < .03) = ", round(prob,3) ))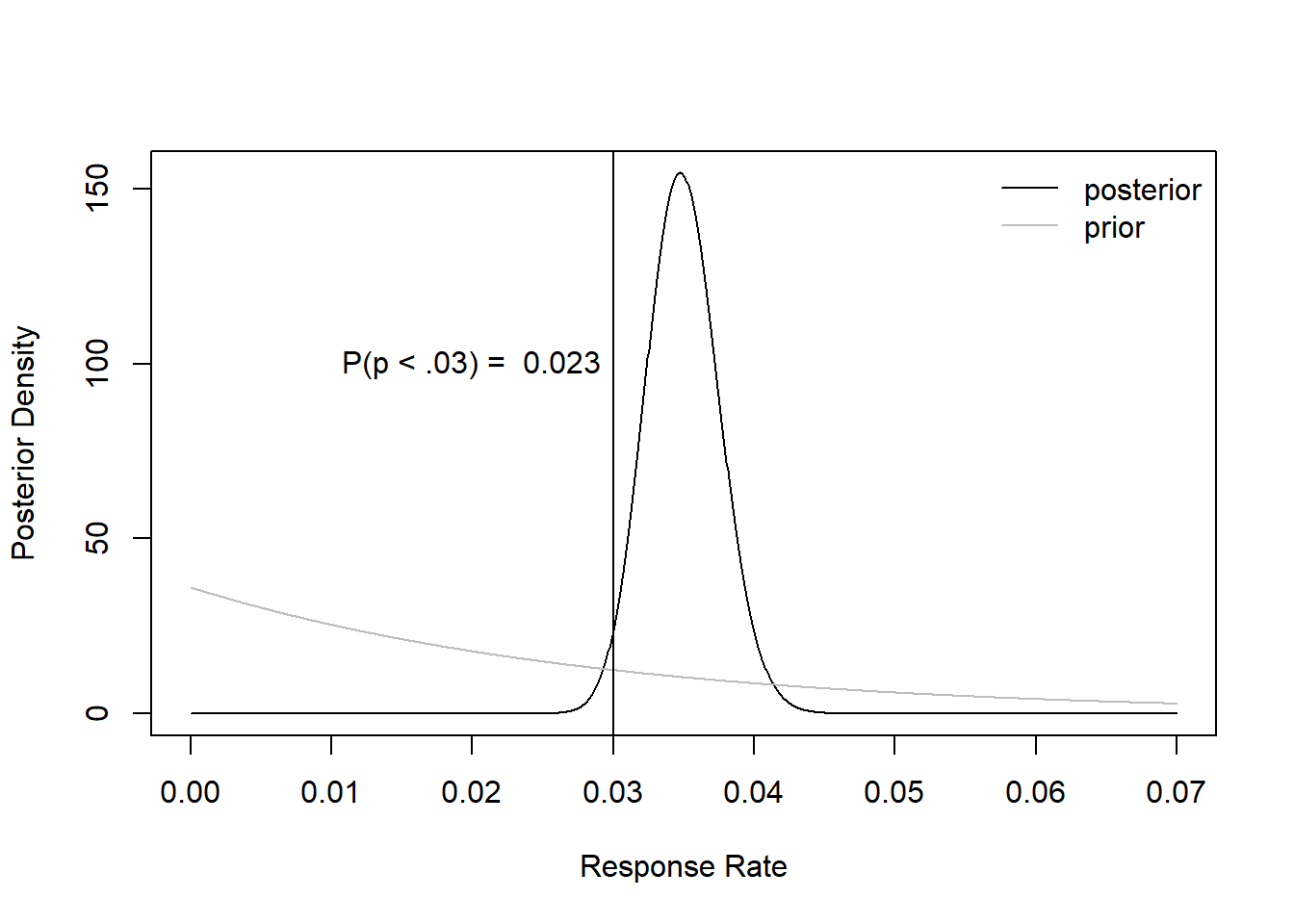

So we know that the probability that our response rate falls below our breakeven point is 0.023, which is highly unlikely.

B. Continuous Example

If the dependent variable is continuous, then we use a normal prior. For example, I would like to know what the mean time-on-site is for the A group and the B group from an A/B test. In particular, we want to study whether those differences are statistically significant or not in order to assess the impact of our experiment.

So, let’s say we have an A/B Test to study Time spend on site (minutes), depending on the design of a company’s homepage. Here our dependent variable is continuous, so we will assume a normal distribution.

Prior

Before I saw this data, I knew nothing about how long people might spend on this website. They might stay for 5 seconds or they might stay for 5 hours. Formally, I can describe my prior beliefs with a prior distribution: \[\textrm{mean time-on-site for group} \sim N(0, 100^2)\]
Here is the picture:

y <- dnorm(-300:300, mean=50, sd=100)
round(qnorm(c(0.025, 0.975), mean=0, sd=100),2)

## [1] -196  196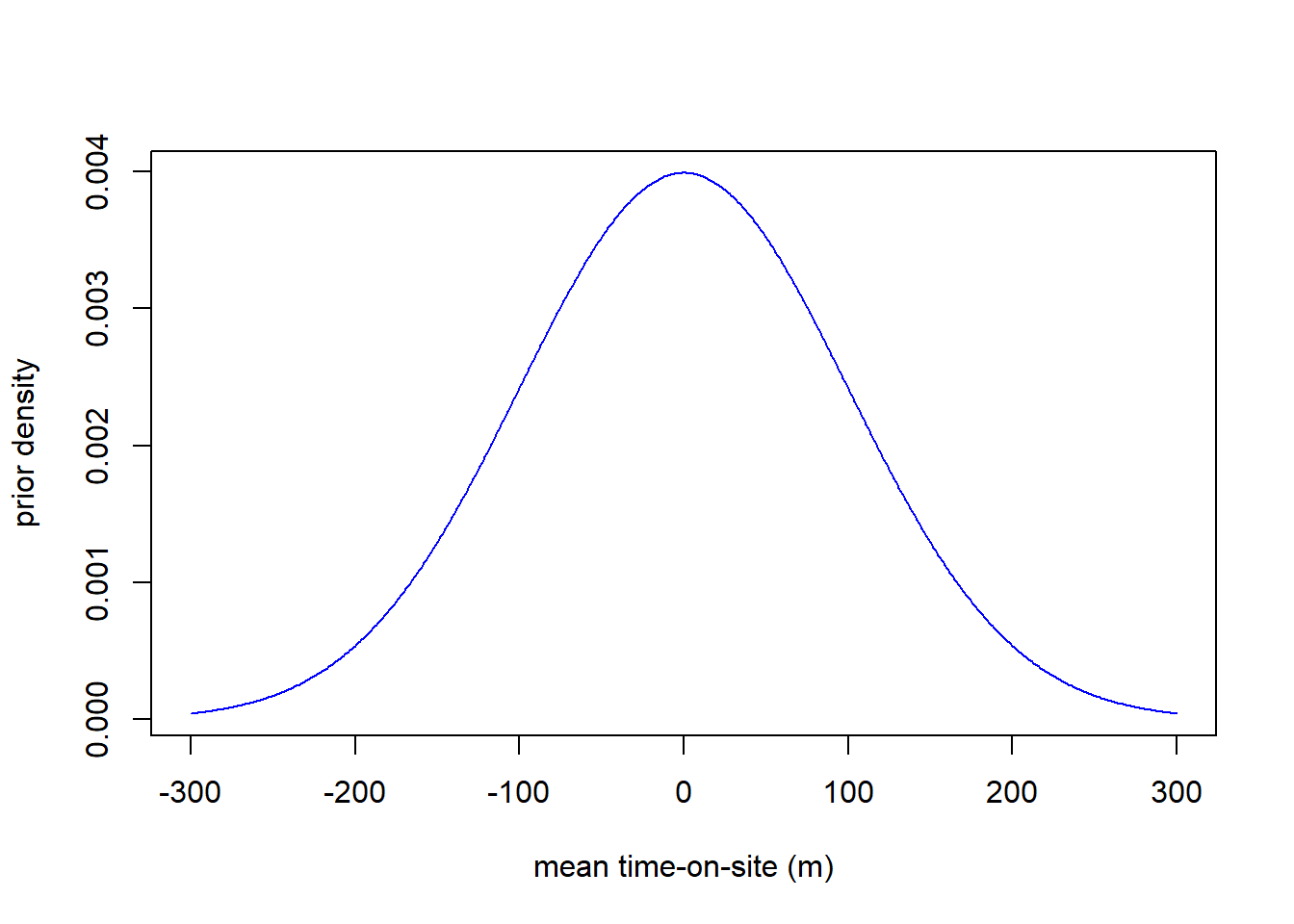

Posterior

Then Bayes rule tells us that the posterior distribution for mean

time-on-site for each group should be:

\[ \textrm{mean time-on-site (m)} \sim \mathcal{N}\left(\mu, \sigma^2\right) \]where

\[ \sigma = \left(\frac{1}{\sigma_{0}^2} + \frac{n}{s^2}\right)^{-1} \]

and

\[ \mu = \sigma^2 \left(\frac{\mu_0}{\sigma_{0}^2} + \frac{n \bar{y}}{s^2}\right) \]

n_A <- sum(test_data$group=="A") # obs for A
n_B <- sum(test_data$group=="B") # obs for B
s <- sd(test_data$time_on_site) # standard deviation of data (approx)

# Posterior standard deviation follows this formula
post_sd_A <- (1/100^2 + n_A/s^2)^-(1/2)
post_sd_B <- (1/100^2 + n_B/s^2)^-(1/2)

# sample mean
ybar_A <- mean(test_data[test_data$group=="A", "time_on_site"])
ybar_B <- mean(test_data[test_data$group=="B", "time_on_site"])

# Posterior mean is just the mean for each group, 
post_mean_A <- post_sd_A^2*(0/100^2 + n_A *ybar_A / s^2)
post_mean_B <- post_sd_B^2*(0/100^2 + n_B *ybar_B / s^2)

We can plot each posterior distribution to compare:

xx=seq(5,6,length=1000) 

plot(x=xx, y=dnorm(xx, mean=post_mean_A, sd=post_sd_A), 
     type="l", col="blue", xlab="mean time-on-site (m)", ylab="posterior density")
lines(x=xx, y=dnorm(xx, mean=post_mean_B, sd=post_sd_B), col="red")
lines(x=xx, y=dnorm(xx, mean=0, sd=100), col="gray")
legend("topright", col=c("blue", "red", "gray"), legend=c("posterior for A", "posterior for B", "prior"), bty="n", lty=1)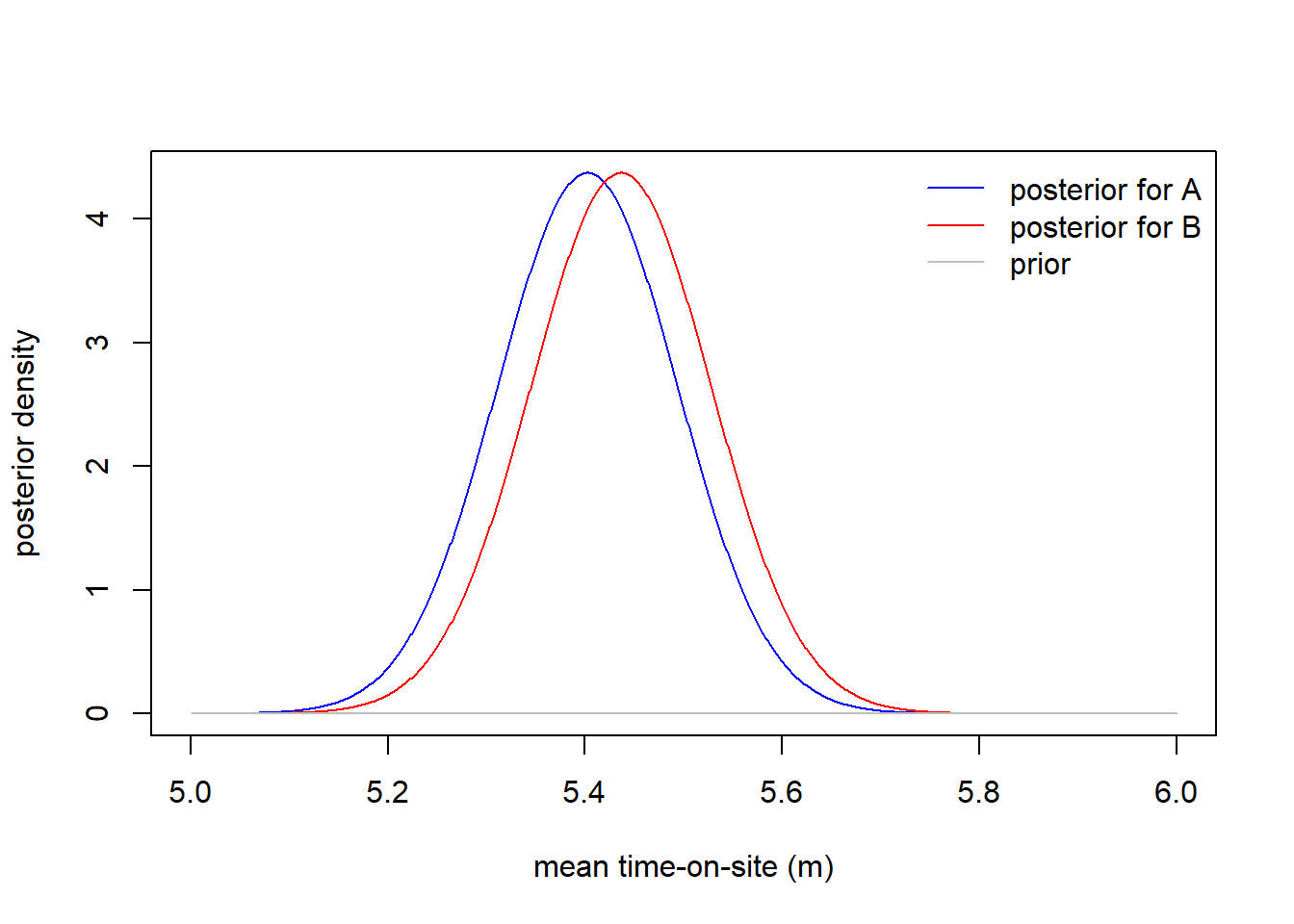

Once we have the distribution for the difference in the mean time-on-site, we can compute the probability that the mean of B is greater than the mean of A:

post_mean_diff <- post_mean_B - post_mean_A
post_sd_diff <- sqrt(post_sd_B^2 + post_sd_A^2)
prob=1-pnorm(0, mean=post_mean_diff, sd=post_sd_diff)

plot(x=(-50:60)/100, y=dnorm((-50:60)/100, mean=post_mean_diff, sd=post_sd_diff), 
     type="l", col="black", 
     xlab="difference in mean time-on-site (m)", ylab="posterior density")
abline(v=0)
text(-0.25, 2.9, "A has higher mean time-on-site")
text(0.35, 2.9, "B has higher mean time-on-site")
text(x = .4,y= 1.9, paste("P(m_A < m_B) = ", round(prob,3) ))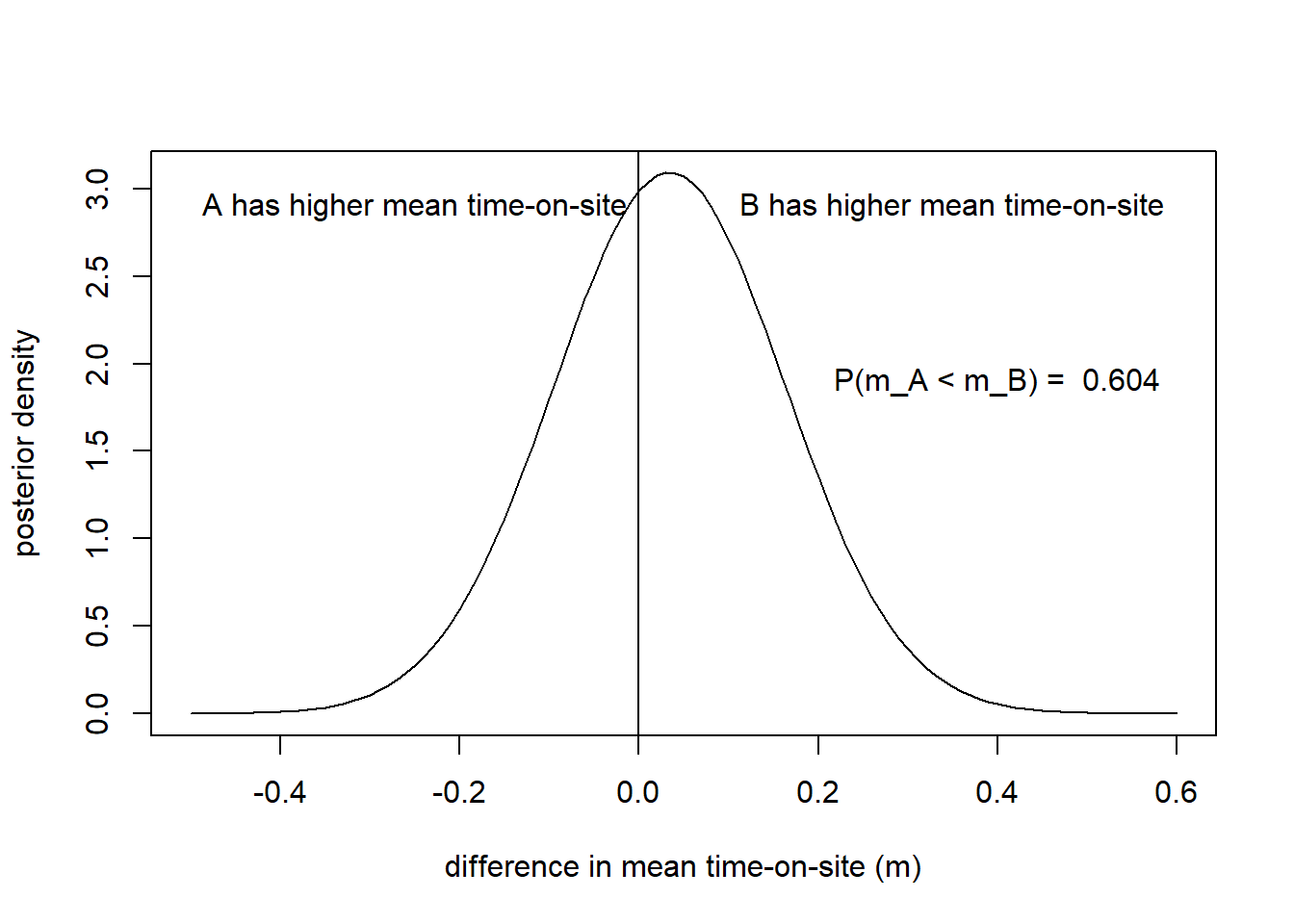

Test & Roll

Finally, when doing Test & Roll Experiments, we want to know how big should the test sample be relative to the rollout sample. This is a maximization problem.

Profit-Maximizing Sample Size

the profit maximizing sample size is:
\[n_1 = n_2 = \sqrt{\frac{N}{4}\left( \frac{s}{\sigma} \right)^2 + \left( \frac{3}{4} \left( \frac{s}{\sigma} \right)^2 \right)^2 } - \frac{3}{4} \left(\frac{s}{\sigma} \right)^2\] This new sample size formula is derived in Feit and Berman (2019) Marketing Science.

Computing the sample size in R

We will work with our conversion rates example. Our data will have the following characteristics:

N <- 100000 # available population
mu <- 0.68  # average conversion rate across previous treatments
sigma <- 0.03 # range of expected conversation rates across previous treatments
s <- sqrt(mu*(1-mu)) # binomial approximation, because is binary

We will use a binomial distribution for binary data. We can calculate the optimal test size:

## Optimal Test Sample Size: 2284